REGRESIÓN MÍNIMO CUADRÁTICA
Introducción
En este capítulo estudiamos dos tipos de problemas. El primero es el de encontrar una función que se ajuste lo mejor posible a un conjunto de puntos observados, gráficamente equivale a encontrar una curva que aunque no pase por todos los puntos esté lo más próxima posible de dichos puntos. El segundo es medir el grado de ajuste entre la función teórica (función ajustada) y la nube de puntos. Distinguimos así, entre Teoría de Regresión y Teoría de Correlación.
- Teoría de Regresión: Consiste en la búsqueda de una “función” que exprese lo mejor posible el tipo de relación entre dos o más variables. Este capítulo sólo estudia la situación de dos variables.
Para seleccionar la curva que mejor se ajusta a la nube de puntos utilizamos el método de los Mínimos Cuadrados.
Una de las aplicaciones más interesante que tiene la Regresión es la de Predecir, es decir, conocido el valor de una de las variables, estimar el valor que presentará la otra variable relacionada con ella. - Teoría de Correlación: Estudia el grado de dependencia entre las variables es decir, su objetivo es medir el grado de ajuste existente entre la función teórica (función ajustada) y la nube de puntos.
Cuando la relación funcional que liga las variables X e Y es una recta entonces la regresión y correlación reciben el nombre de Regresión Lineal y Correlación Lineal. Una medida de la Correlación Lineal la da el Coeficiente de Correlación Lineal de Pearson.
Rectas de regresión o de mínimos cuadrados
Distinguiremos entre dos rectas de regresión: La Recta de Regresión Y sobre X y la Recta de Regresión X sobre Y.
Rectas de regresión Y sobre X
Vamos a determinar entre todas las rectas que tienen como ecuación general \( y=bx+a \), aquella que, según el procedimiento de Mínimos Cuadrados, mejor se ajusta a la nube de puntos de la distribución bidimensional.
Supongamos que la función que expresa el comportamiento de Y en relación con X, tiene la siguiente expresión:
\( y=bx+a \)
donde a y b son dos parámetros desconocidos. Para determinar estos parámetros se utiliza el procedimiento de Mínimos Cuadrados, dicho procedimiento consiste en minimizar la expresión
\( S(a,b)=\sum_{i}\sum_{j}f_{ij} \left (y_{j}-(bx_{i}+a) \right)^2 \)
siendo \( bx_{i}+a \) la ordenada teórica o estimada por la recta que se denota por \( y_{i} \). De esta forma la expresión anterior se transforma en
\( S(a,b)=\sum_{i}\sum_{j}f_{ij}(y_{j}-y_{i})^2 \)
Recibe el nombre de Residuos, y se denotan por \( e_{ij} \), a la diferencia entre el valor \( y_{j} \) (valor real observado asociado a \( x_{i} \)) y el valor \( \hat{y}_{j} \) (valor teórico asociado a \( x_{i} \)): \( e_{ij}=y_{j}- \hat{y}_{j} \)
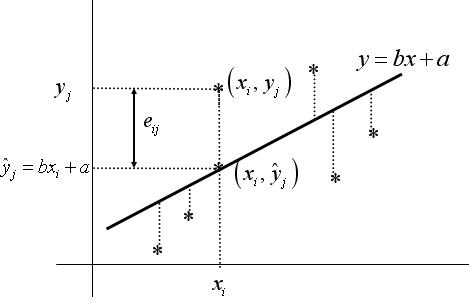
Figura 3.1: Recta de regresión Y/X
El criterio de Mínimos Cuadrados considera que la función que mejor se ajusta a los datos es aquella función que minimiza la media de los cuadrados de los residuos, es decir, que minimiza la siguiente expresión:
\( S(a,b)=\sum_{i}\sum_{j}f_{ij}e_{ij}^2=\sum_{i}\sum_{j}f_{ij} \left (y_{j}-(bx_{i}+a) \right)^2 \)
La condición necesaria para la existencia de mínimo es que las primeras derivadas parciales respecto a cada uno de los parámetros se anulen
\( \begin{array} {c} \displaystyle \frac{∂S}{∂a}=2\sum_{i,j}f_{ij}(y_{j}-bx_{i}-a)(-1)=0 \\ & \\ \displaystyle \frac{∂S}{∂b}=2\sum_{i,j}f_{ij}(y_{j}-bx_{i}-a)(-x_{i})=0 \\ \end{array} \)
Estas ecuaciones reciben el nombre de Ecuaciones Normales y a partir de este sistema de ecuaciones se obtienen los parámetros a y b
\( a= \bar{y}- \displaystyle \frac{σ_{xy}}{σ_{x}^2} \bar{x} \hspace{.3cm} ; \hspace{.3cm} b= \displaystyle \frac{σ_{xy}}{σ_{x}^2} \)
En efecto, del sistema de ecuaciones anterior se obtiene
\( \begin{array} {c} \displaystyle \sum_{i,j}f_{ij}y_{j}= b \displaystyle \sum_{i,j}f_{ij}x_{i}+a \displaystyle \sum_{i,j}f_{ij} \\ \displaystyle \sum_{i,j}f_{ij}y_{j}x_{i}=b\displaystyle \sum_{i,j}f_{ij}x_{i}^2+a\displaystyle \sum_{i,j}f_{ij}x_{i} \\ \end{array} \) \( \Rightarrow \begin{array} {c} \bar{y}=b \bar{x}+a \Rightarrow a=\bar{y}-b \bar{x} \\ \displaystyle \sum_{i,j}f_{ij}y_{j}x_{i}=b\displaystyle \sum_{i,j}f_{ij}x_{i}^2+a\bar{x}\\ \end{array} \)Sustituyendo el valor de a en la segunda ecuación se tiene
\( \displaystyle \sum_{i,j}f_{ij}y_{j}x_{i}=b\displaystyle \sum_{i,j}f_{ij}x_{i}^2+ \bar{y}\bar{x}-b\bar{x}^2 \Rightarrow \displaystyle \sum_{i,j}f_{ij}y_{j}x_{i}-\bar{y}\bar{x}=b \left( \displaystyle \sum_{i,j}f_{ij}x_{i}^2- \bar{x}^2 \right) \)
Entonces
\( b= \displaystyle \frac{σ_{xy}}{σ_{x}^2} \hspace{.6cm} y \hspace{.6cm} a= \bar{y}-b \bar{x}= \bar{y}- \displaystyle \frac{σ_{xy}}{σ_{x}^2} \bar{x} \)
Por tanto, la Recta de Regresión Y sobre X tiene la siguiente ecuación:
\( y-\bar{y}= \displaystyle \frac{σ_{xy}}{σ_{x}^2}(x-\bar{x}) \)
Se llama Coeficiente de Regresión de Y sobre X, y se denota por \( b_{yx} \), al cociente
\( b_{yx}= \displaystyle \frac{σ_{xy}}{σ_{x}^2} \)
que representa la variación de Y si X aumenta en una unidad.
Una de las aplicaciones de la recta de regresión Y sobre X es predecir el valor de Y conocido el valor de X. Si nuestro objetivo es predecir el valor de X conocido el valor de Y es necesario utilizar la recta de regresión X sobre Y.
Rectas de regresión X sobre Y
Para obtener la recta de regresión X sobre Y se procede de forma análoga al apartado anterior, repitiendo el método de Mínimos Cuadrados sobre la media de los cuadrados de los residuos, que en este caso, tiene la siguiente expresión:
\( S^{∗}(a^′,b^′)=\displaystyle \sum_{i}\displaystyle \sum_{j}f_{ij}e_{ij}^2=\displaystyle \sum_{i,j}f_{ij}(x_{i}-\hat{x}_{i})^2= \displaystyle \sum_{i,j}f_{ij}\left (x_{i}-(b′y_{j}+a′)\right)^2 \)
resultando la siguiente expresión de la recta de regresión X sobre Y
\( x-\bar{x}= \displaystyle \frac{σ_{xy}}{σ_{y}^2}(y-\bar{y}) \)
Que, como hemos dicho anteriormente, una de sus aplicaciones es predecir el valor de X conocido el valor de Y.
Se llama Coeficiente de Regresión de X sobre Y, y se denota por \( b_{xy}\), al cociente
\( b_{xy}= \displaystyle \frac{σ_{xy}}{σ_{y}^2} \)
que representa la variación de X si Y aumenta en una unidad.
Sabemos que el signo del valor de la covarianza nos indica el sentido de la relación entre las variables y recíprocamente. Pero el valor de la covarianza depende de las unidades en que vengan expresadas las variables. Así pues, es necesario definir un coeficiente que mida el grado de variación conjunta entre las variables y no esté afectado por las unidades de medida. Una forma de obtener esta medida es dividir la covarianza por el producto de las desviaciones típicas de cada variable, dando como resultado un coeficiente adimensional que denotamos por r y recibe el nombre de Coeficiente de Correlación Lineal de Pearson.
Coeficiente de correlación lineal de Pearson
Se define el Coeficiente de Correlación Lineal de Pearson, y se denota por r, como el cociente entre la covarianza y la desviación típica de cada variable
\( r= \displaystyle \frac{σ_{xy}}{σ_{x}σ_{y}} \hspace{.3cm} ; \hspace{.3cm} -1≤ r ≤1 \)
Propiedades
- Es un coeficiente adimensional (carece de unidades de medida)
- Es invariante frente a los cambios de origen y escala de las variables. Supongamos los cambios de variables:
\( \begin{array} {c} x_{i}^′= \displaystyle \frac{x_{i}-x_0}{a} \\ y_{j}^′= \displaystyle \frac{y_{j}-y_0}{b} \\ \end{array} \) \( \Rightarrow r^′= \displaystyle \frac{σ_{xy}^′}{σ_{x}^′σ_{y}^′}= \displaystyle \frac{ \displaystyle \frac{σ_{xy}}{ab}}{\displaystyle \frac{σ_{x}}{a}× \displaystyle \frac{σ_{y}}{b}} = \displaystyle \frac{σ_{xy}}{σ_{x}σ_{y}}=r \)
- Si \( r=0 \) o \( r≈0 \), puede afirmarse que no existe relación lineal entre las variables
- Si \( |r| \) está próximo a 1 se dice que existe una relación lineal muy fuerte entre las variables
- Si \( r = \pm 1 \Rightarrow \) las observaciones de ambas variables están perfectamente alineadas, puede afirmarse que hay dependencia funcional lineal entre las variables. El signo de r, coincide con el de \( σ_{xy} \), nos indica el crecimiento o decrecimiento de la recta
- Si \( r>0 \Rightarrow \) Dependencia directa
- Si \( r<0 \Rightarrow \) Dependencia inversa
Elevando el coeficiente de correlación lineal de Pearson al cuadrado tenemos:
\( r^2= \displaystyle \frac{σ_{xy}^2}{σ_{x}^2σ_{y}^2}= \displaystyle \frac{σ_{xy}}{σ_{x}^2}× \displaystyle \frac{σ_{xy}}{σ_{y}^2}=b_{yx}.b_{xy} \Rightarrow r = \displaystyle \sqrt {b_{yx}.b_{xy}} \)
el signo que se elige en la raíz es el signo de la covarianza.
Utilizando el coeficiente de correlación lineal, las Rectas de Regresión Y/X y X/Y también se pueden expresar, respectivamente, de la siguiente forma:
\( y- \bar{y} =r \displaystyle \frac{σ_{y}}{σ_{x}}(x- \bar{x}) \hspace{.3cm}; \hspace{.3cm} x- \bar{x}=r \displaystyle \frac{σ_{x}}{σ_{y}}(y-\bar{y}) \)
Posición relativa de las rectas de regresión
Las expresiones de las rectas de regresión Y/X y X/Y
\( s \equiv y-\bar{y} = \displaystyle \frac{σ_{xy}}{σ_{x}^2}(x-\bar{x}) \)
\( s^′ \equiv x- \bar{x} = \displaystyle \frac{σ_{xy}}{σ_{y}^2}(y-\bar{y}) \)
indican que pasan por el punto (x,y), por tanto sólo pueden presentar dos posiciones en el plano:
i) Se cortan sólo en ese punto
ii) Coincidan: Dichas rectas coinciden cuando, además de tener el punto (x,y) en común, tienen la misma pendiente. Es decir, las pendientes \( m_{s}= \displaystyle \frac{σ_{xy}}{σ_{x}^2}\) y \( m_{s}^′= \displaystyle \frac{σ_{y}^2}{σ_{xy}} \) de las rectas de regresión son iguales
\( \displaystyle \frac{σ_{xy}}{σ_{x}^2}= \displaystyle \frac{σ_{y}^2}{σ_{xy}} \Leftrightarrow \displaystyle \frac{σ_{xy}^2}{σ_{x}^2σ_{y}^2}=1 \Leftrightarrow r^2=1 \)
Por lo tanto
- Si \( r^2=1 \Rightarrow \) Las rectas de regresión coinciden
- Si \( r^2 \neq 1 \Rightarrow \) Las rectas de regresión se cortan en el punto (x, y)
Ejemplo 3.1: Dada la siguiente distribución bidimensional
\( \begin{array} {|l|c|c|c|c|} \hline X/Y & 1 & 2 & 3 & 4 \\ \hline 10 & 1 & 3 & 0 & 0 \\ \hline 12 & 0 & 1 & 4 & 3 \\ \hline 14 & 2 & 0 & 0 & 2 \\ \hline 16 & 4 & 0 & 0 & 0 \\ \hline \end{array} \)
Se pide:
a) ¿Son independientes X e Y?
b) Dar las expresiones de las rectas de regresión de Y/X y de X/Y
c) Determinar el coeficiente de correlación lineal.
Respuesta:
\( \begin{array} {|l|c|c|c|c|c|c|c|r|} \hline x_{i}/y_{j} & 1 & 2 & 3 & 4 & n_{i.} & x_{i}n_{i.} & x_{i}^2n_{i.} & \sum_{j}x_{i}y_{j}n_{ij} \\ \hline 10 & 1 & 3 & 0 & 0 & 4 & 40 & 400 & 10+60+0+0=70 \\ \hline 12 & 0 & 1 & 4 & 3 & 8 & 96 & 1152 & 0+24+144+144=312 \\ \hline 14 & 2 & 0 & 0 & 2 & 4 & 56 & 784 & 28+0+0+112=140 \\ \hline 16 & 4 & 0 & 0 & 0 & 4 & 64 & 1024 & 64+0+0+0=64 \\ \hline n_{.j} & 7 & 4 & 4 & 5 & 20 & 256 & 3360 & 586 \\ \hline y_{j}n_{.j} & 7 & 8 & 12 & 20 & 47 & & & \\ \hline y_{j}^2 n_{.j} & 7 & 16 & 36 & 80 & 139 & & & \\ \hline \end{array} \)
a) Para que X e Y sean independientes se tiene que verificar:
\( n_{ij}= \displaystyle \frac{n_{i.}n_{.j}}{n} \hspace{.3cm}; \hspace{.3cm} n_{11}=1 \neq \displaystyle \frac{4×7}{20}\Rightarrow \) No son independientes
o bien comprobando si las columnas (filas) son proporcionales.
b) Dar las expresiones de las rectas de regresión de Y/X y de X/Y
\( \bar{x}= \displaystyle \frac{256}{20}=12.8 \hspace{.3cm}; \hspace{.3cm} \bar{y}= \displaystyle \frac{47}{20}=2.35 \)
\( σ_{x}^2= \displaystyle \frac{3360}{20}-(12.8)^2=4.16⇒σ_{x}=2.039 \)
\( σ_{y}²= \displaystyle \frac{139}{20}-(2.35)^2=1.43=σ_{y}^2 \Rightarrow σ_{y}=1.195 \)
\( σ_{xy}= \displaystyle \frac{586}{20}-(12.8)×(2.35)=-0.78 \)
∙ Recta de regresión de Y/X
\( y-\bar{y}= \displaystyle \frac{σ_{xy}}{σ_{x}^2}(x-\bar{x}) \Rightarrow y-2.35= \displaystyle \frac{-0.78}{4.16}(x-12.8) \)
∙ Recta de regresión de X/Y
\( x-\bar{x}= \displaystyle \frac{σ_{xy}}{σ_{y}^2}(y-\bar{y}) \Rightarrow x-12.8= \displaystyle \frac{-0.78}{1.43}(y-2.35) \)
c) Determinar el coeficiente de correlación lineal.
\( r= \displaystyle \frac{σ_{xy}}{σ_{x}σ_{y}}= \displaystyle \frac{-0.78}{2.039×1.195}=-0.320 \)
La correlación es negativa, las variables están relacionadas en sentido opuesto (si una variable aumenta de valor la otra variable disminuye). El coeficiente de correlación es demasiado pequeño, por tanto no se ha realizado un buen ajuste por medio de una recta de mínimos cuadrados.
Coeficiente de determinación y varianza residual
Hemos visto en la sección anterior que el criterio de mínimos cuadrados utiliza como medida del error que se comete, cuando se ajusta una curva a la nube de puntos, la media de los cuadrados de los residuos, esta media recibe el nombre de Varianza Residual.
La Varianza residual se utiliza como medida de la bondad del ajuste, cuanto menor sea la Varianza Residual, menores serán los residuos y por lo tanto mejor será el ajuste de la curva a la nube de puntos. Pero presenta el problema de no saber a partir de que valores dicha varianza es suficientemente pequeña o suficientemente grande para considerar que el ajuste realizado es un buen o un mal ajuste. Ese problema se soluciona mediante el Coeficiente de Determinación.
La definición del Coeficiente de Determinación o Razón de Correlación se basa en la descomposición de la varianza marginal de Y, V(y) en
\( \sum_{i}\sum_{j}f_{ij}(y_{j}-\bar{y})^2=\sum_{i}\sum_{j}f_{ij}(y_{j}- \hat{y}_{i})^2+\sum_{i}\sum_{j}f_{ij}(\hat{y}_{i}-\bar{y})^2 \hspace{.3cm} [1] \)
Esta descomposición [1] sólo es válida cuando se realiza en funciones que son lineales en los parámetros (recta, parábola, hipérbola equilátera,⋯)
donde
- \( \sum_{i}\sum_{j}f_{ij}(y_{j}-y)^2 \) es la Varianza Marginal de Y que se denota por \( V(y) \) o \( σ_{y}^2 \)
- \( \sum_{i}\sum_{j}f_{ij}(y_{j}-y_{i})^2 \) es la Varianza Residual de Y, \( V_{r}(y) \), también llamada Varianza no Explicada, y representa las desviaciones que no se han podido explicar mediante la regresión
- \( \sum_{i}\sum_{j}f_{ij}(y_{i}-y)^2 \) es la Varianza Explicada por la regresión que se denota por \( V_{e}(y) \)
Por lo tanto, la descomposición [1] se puede expresar como
\( V(y)=V_{r}(y)+V_{e}(y) \)
Se define el Coeficiente de Determinación (o Razón de Correlación), que vamos a denotar de forma general por \( R^2 \), como el cociente entre la Varianza Explicada por la regresión y la Varianza marginal de y
\( R^2= \displaystyle \frac{V_{e}(y)}{V(y)}= \displaystyle \frac{V(y)-V_{r}(y)}{V(y)}=1- \displaystyle \frac{V_{r}(y)}{V(y)} \Rightarrow 0 \leq R^2 \leq 1, \)
y se puede interpretar como la proporción de la varianza marginal de Y, V(y), que es explicada por la regresión.
- Si \( R^2=0 \Rightarrow \displaystyle \frac{V_{r}(y)}{V(y)}=1 \Rightarrow V_{r}(y)=V(y) \Rightarrow V_{e}(y)=0 \Rightarrow \) El modelo no explica nada de Y a partir de X, por tanto es el peor ajuste que puede hacerse por el procedimiento de mínimos cuadrados
- Si \( R^2=1 \Rightarrow \displaystyle \frac{V_{r}(y)}{V(y)}=0 \Rightarrow V_{r}(y)=0 \Rightarrow \) Todos los residuos son nulos, todos los puntos de la nube de puntos están sobre la curva, en este caso el ajuste es perfecto. Y depende funcionalmente de X
- Si \( 0<R^2<1 \Rightarrow \)
- Si \( R^2 \) se aproxima a 1 nos indicará buen ajuste
- Si \( R^2 \) se aproxima a 0 nos indicará mal ajuste
1) En la recta de regresión de Y/X, la Varianza Residual se denota por \( V_{r}(y) \) y se comprueba que
\( V_{r}(y)=V(y)(1-r^2) \)
Entonces, el coeficiente de determinación es
\( R^2=1- \displaystyle \frac{V_{r}(y)}{V(y)}=1- \displaystyle \frac{V(y)(1-r^2)}{V(y)}=r^2 \)
2) En la recta de regresión de X/Y, la Varianza Residual se denota por \( V_{r}(x) \) y se comprueba que
\( V_{r}(x)=V(x)(1-r^2) \)
Entonces, el coeficiente de determinación
\( R^2=1- \displaystyle \frac{V_{r}(x)}{V(x)}=1- \displaystyle \frac{V(x)(1-r^2)}{V(x)}=r^2 \)
Por lo tanto el coeficiente de correlación lineal al cuadrado, \( r^2 \), se utiliza como medida de la bondad del ajuste de la recta de mínimos cuadrados.
Ejemplo 3.2: Las notas de física (X) y en matemáticas (Y) obtenidas por 10 alumnos elegidos al azar en un curso de un centro docente han sido las siguientes (según el orden de selección de la muestra)
\( \begin{array} {|l|c|c|c|c|c|c|c|c|c|c|} \hline N^{o} de \hspace{.1cm } orden & 1^{o} & 2^{o} & 3^{o} & 4^{o} & 5^{o} & 6^{o} & 7^{o} & 8^{o} & 9^{o} & 10^{o} \\ \hline X_{i}& 9 & 7 & 3 & 6 & 7 & 5 & 10 & 8 & 2 & 5 \\ \hline Y_{i} & 8 & 5 & 4 & 2 & 9 & 6 & 10 & 9 & 1 & 5 \\ \hline \end{array} \)
a) Estimar los parámetros de la recta de regresión de Y/X
b) Estimar los parámetros de la recta de regresión de X/Y
c) Calcular el coeficiente de determinación y el de correlación lineal entre X e Y
d) Calcular la varianza residual en la regresión de Y/X
e) Calcular la varianza residual en la regresión de X/Y
f) Representar gráficamente ambas rectas de regresión
g) Para un alumno que haya obtenido un 4 en físicas ¿Qué nota le pronosticaría en matemáticas?
h) Para un alumno que haya obtenido un 7 en matemáticas ¿Qué nota le pronosticaría en físicas?
Respuesta:
\( \begin{array} {|l|c|c|c|c|} \hline x_{i} & y_{i} & x_{i}^2 & x_{i}y_{i} & y_{i}^2 \\ \hline 9 & 8 & 81 & 72 & 64 \\ \hline 7 & 5 & 49 & 35 & 25 \\ \hline 3 & 4 & 9 & 12 & 16 \\ \hline 6 & 2 & 36 & 12 & 4 \\ \hline 7 & 9 & 49 & 63 & 81 \\ \hline 5 & 6 & 25 & 30 & 36 \\ \hline 10 & 10 & 100 & 100 & 100 \\ \hline 8 & 9 & 64 & 72 & 81 \\ \hline 2 & 1 & 4 & 2 & 1 \\ \hline 5 & 5 & 25 & 25 & 25 \\ \hline 62 & 59 & 442 & 423 & 433 \\ \hline \end{array} \)
\( \begin{array} {ccccccc} \bar{x}= \displaystyle \frac{62}{10}=6.2 &; & \bar{y}=\displaystyle \frac{59}{10}=5.9 & ; & σ_{x}^2= \displaystyle \frac{442}{10}- \left(\displaystyle \frac{62}{10}\right)^2=5.76 & ; & σ_{y}^2= \displaystyle \frac{433}{10}-\left( \displaystyle \frac{59}{10}\right)^2=8.49 \\ \end{array} \)
\(σ_{xy}= \displaystyle \frac{423}{10}- \left( \displaystyle \frac{62}{10}\right)× \left( \displaystyle \frac{59}{10}\right)=5.72 \)
a) Parámetros de la recta de regresión de Y/X
\( y=a+bx \Rightarrow \begin{array} {ll} & b= \displaystyle \frac{σ_{xy}}{σ_{x}^2}= \displaystyle \frac{5.72}{5.76}=0.99 \\ \\ & a=\bar{y}-b \bar{x}=5.9- (0.99)×(6.2)=-0.238 \\ \end{array} \)
La recta de regresión de Y/ X tiene la siguiente ecuación:
\( y=-0.238+0.99x \)
b) Parámetros de la recta de regresión de X/Y
\( x=a′+b′y \Rightarrow \begin{array} {ll} & b^´ = \displaystyle \frac{σ_{xy}}{σ_{y}^2}= \displaystyle \frac{5.72}{8.49}=0.67 \\ \\ & a^´ =\bar{x}-b^´ \bar{y}=6.2-(0.67)×(5.9)=2.247 \\ \end{array} \)
La recta de regresión de X/ Y tiene la siguiente ecuación:
\( x=2.247+0.67y \)
c) Calcular el coeficiente de determinación y el de correlación lineal entre X e Y
Coeficiente de determinación
\( R^2= \displaystyle \frac{σ_{xy}^2}{σ_{}^2 σ_{y}^2}= \displaystyle \frac{5.72^2}{(5.76×8.49)}=0.669 \)
Coeficiente de correlación lineal de Pearson
\( r= \displaystyle \frac{σ_{xy}}{σ_{x}σ_{y}}=0.818 \)
d) Varianza residual de la recta de regresión de Y/X
\( V_{r}(y)=V(y)(1-r^2)=8.49(1-0.669)=2.8109 \)
e) Varianza residual de la recta de regresión de X/Y
\( V_{r}(x)=V(x)(1-r^2)=5.76(1-0.669)=1.9276 \)
f) Representar gráficamente ambas rectas de regresión
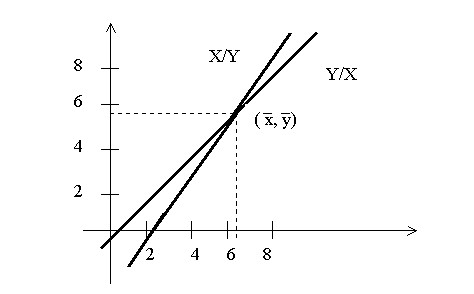
Figura 3.2: Rectas de regresió Y/X y X/Y
g) Para un alumno que haya obtenido un 4 en físicas ¿Qué nota le pronosticaría en matemáticas?
\( y_{x=4}=-0.238+4×0.99=3.72 \)
h) Para un alumno que haya obtenido un 7 en matemáticas ¿Qué nota le pronosticaría en físicas?
\( x_{y=7}=2.247+7×0.67=6.93 \)
Algunos valores particulares de r y r²
Recordemos que el coeficiente de correlación lineal de Pearson tiene la siguiente expresión:
\( r= \displaystyle \frac{σ_{xy}}{σ_{x}σ_{y}} \)
1) Si \( r=0 \Rightarrow σ_{xy}=0 \) y por lo tanto las rectas de regresión
\( y-\bar{y}= \displaystyle \frac{σ_{xy}}{σ_{x}^2}(x-\bar{x}) \)
\( x- \bar{x}= \displaystyle \frac{σ_{xy}}{σ_{y}^2}(y-\bar{y}) \)
se transforman en:
\( y=\bar{y} \)
\( x=\bar{x} \)
Las rectas de regresión son paralelas a los ejes coordenados y perpendiculares entre sí. Indican que no existe relación lineal entre las variables X e Y, pero dichas variables pueden estar relacionadas por otro tipo de función.
- Se demuestra que: Si las variables X e Y son independientes entonces \( r=0 \), sin embargo el recíproco no se puede afirmar. Es decir,
- Si X e Y son independientes \( \Rightarrow r=0 \) (Figura 3.3)
- Si \( r=0 \Rightarrow \) que X e Y son independientes (Figura 3.4)
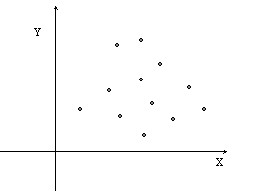 Figura 3.4: r = 0 entonces X e Y independientes
Figura 3.4: r = 0 entonces X e Y independientes
Figura 3.5: r=0 pero X e Y no son independientes
- La Figura 3.4 muestra una distribución bidimensional en la que r=0 y las variable X e Y son independientes
- La Figura 3.5 muestra una distribución bidimensional en la que r=0 pero las variable X e Y están relacionadas aunque no linealmente.
2) Si \( r= \pm 1 \Rightarrow r^2 =1 \Rightarrow V_{r}(y)=0 \Rightarrow \) Todos los residuos son ceros y por tanto todos los puntos de la nube de puntos están sobre la recta de regresión (los valores observados coinciden con los valores teóricos) \( \Rightarrow \) Las dos rectas de regresión coinciden. En este caso se dice que la correlación es perfecta.
- Si \( r=1 \Rightarrow \) La pendiente de la recta es positiva. La correlación es perfecta y directa o positiva. Existe dependencia funcional entre las variables
- Si \( r=-1 \Rightarrow \) La pendiente de la recta es negativa. La correlación es perfecta e inversa o negativa. Existe dependencia funcional entre las variables
3) \( -1<r<0 \hspace{.2cm} \) o \( \hspace{.2cm} 0<r<1 \)
3a) Si el coeficiente de regresión se aproxima a la unidad en valor absoluto indica que la dependencia estadística es muy grande y por tanto existe un buen ajuste por medio de la recta de mínimos cuadrados
3b) Si el coeficiente de regresión se aproxima a 0 en valor absoluto indica que las rectas de regresión forman un ángulo de 90º y a medida que r se aleja de cero el ángulo que forman las rectas se va aproximando a 0º, haciéndose 0º cuando \( r=±1 \)
3c) \( 0<r<1 \Rightarrow \) La correlación es positiva (valores altos (bajos) de una variable le corresponden valores altos (bajos) de la otra variable)
3d) \( -1<r<0 \Rightarrow \) La correlación es negativa (valores altos (bajos) de una variable le corresponden valores bajos (altos) de la otra variable)
∗) \( r^2: \) Se utiliza para medir la bondad del ajuste realizado en la recta de regresión
\( (0 \leq r^2 \leq 1) \)
∗) \( r: \) Se utiliza para medir el grado de asociación lineal entre las dos variables
\( (-1<r<1) \)
Otros tipos de ajuste
En esta sección estudiamos el ajuste de las funciones no-lineales, más utilizadas, a los puntos de la nube de puntos y este estudio lo haremos utilizando ejemplos numéricos.
Parábola
Suponemos que la curva que mejor se ajusta a la nube de puntos es de tipo parabólico, de ecuación
\( y=a+bx+cx^2 \hspace{.3cm}; \hspace{.3cm}a,b,c \in R \)
El criterio de Mínimos Cuadrados considera que la función que mejor se ajusta a los datos es aquella función que minimiza la media de los cuadrados de los residuos. (Hacemos el desarrollo para el caso en que las frecuencias absolutas son unitarias)
\( S(a,b)=\sum_{i,j}e_{ij}^2=\sum_{i,j}(y_{j}-(a+bx_{i}+cx_{i}^2))^2 \)
La condición necesaria para la existencia de mínimo es que las derivadas parciales respecto a cada uno de los parámetros se anulen
\( \begin{array} {c} \displaystyle \frac{\partial S}{\partial a}=2\sum_{i,j}(y_{j}-a-bx_{i}-cx_{i}^2)(-1)=0 \\ \displaystyle \frac{\partial S} {\partial b}=2\sum_{i,j}(y_{j}-a-bx_{i}-cx_{i}^2)(-x_{i})=0 \\ \displaystyle \frac{\partial S}{\partial c}=2\sum_{i,j}(y_{j}-a-bx_{i}-cx_{i}^2)(-x_{i}^2)=0 \\ \end{array} \)
El sistema de ecuaciones normales se convierte en:
\( \begin{array} {lcl} \sum_{j}y_{j} & = & na+b \sum_{i}x_{i}+c \sum_{i}x_{i}^2 \\ \sum_{i,j}y_{j}x_{i} & = & a\sum_{i}x_{i}+b\sum_{i}x_{i}^2+c\sum_{i}x_{i}^3 \\ \sum_{i,j}y_{j}x_{i}^2 & = & a\sum_{i}x_{i}^2+b\sum_{i}x_{i}^3+c \sum_{i}x_{i}^4 \\ \end{array} \)
Resolviendo este sistema de ecuaciones se obtienen los parámetros: a, b y c.
Ejemplo 3.3: Dada la siguiente distribución
\( \begin{array} {|l|c|c|c|c|c|c|} \hline x_{i} & 2 & 3 & 5 & 6 & 9 & 11 \\ \hline y_{i} & 7 & 5 & 9 & 11 & 8 & 10 \\ \hline \end{array} \)
Ajustar a dichos puntos una parábola de \( 2^{º} \) grado: \( y=a+bx+cx^2 \) .
Respuesta:
Realizamos el siguiente cambio de variable: \( x_{i}^′=x_{i}- \bar{x}=x_{i}-6 \)
Por lo tanto, se tiene que ajustar la siguiente parábola: \( y=a+bx^′+cx^{′2} \)
\( \begin{array} {|c|c|c|c|c|c|c|c|} \hline x_{i} & y_{i} & x_{i}^′ & x_{i}^{′2} & x_{i}^{′3} & x_{i}^{′4} & x_{i}^′y_{i} & x_{i}^{′2}y_{i} \\ \hline 2 & 7 & -4 & 16 & -64 & 256 & -28 & 112 \\ \hline 3 & 5 & -3 & 9 & -27 & 81 & -15 & 45 \\ \hline 5 & 9 & -1 & 1 & -1 & 1 & -9 & 9 \\ \hline 6 & 11 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 9 & 8 & 3 & 9 & 27 & 81 & 24 & 72 \\ \hline 11 & 10 & 5 & 25 & 125 & 625 & 50 & 250 \\ \hline 36 & 50 & 0 & 60 & 60 & 1044 & 22 & 488 \\ \hline \end{array} \)
El sistema de ecuaciones normales:
\( \begin{array} {lcl} \sum_{j}y_{j} & = & na+b \sum_{i}x_{i}^′+c \sum_{i}x_{i}^{′2} \\ \sum_{i,j}y_{j}x_{i}^′ & = & a \sum_{i}x_{i}^′+b \sum_{i}x_{i}^{′2}+c \sum_{i}x_{i}^{′3} \\ \sum_{i,j}y_{j}x_{i}^{′2} & = & a \sum_{i}x_{i}^{′2}+b \sum_{i}x_{i}^{′3}+c \sum_{i}x_{i}^{′4} \\ \end{array} \)queda de la siguiente forma
\( \begin{array} {lcl} 50 & = & 6a+0b+60c \\ 22 & = & 0a+60b+60c \\ 488 & = & 60a+60b+1044c \\ \end{array} \) \( \Rightarrow \hspace{.3cm} \begin{array} {lcl} 25& = & 3a+30c \\ 11& = & 30b+30c \\ 122 & = & 15a+15b+261c \\ \end{array} \Rightarrow \hspace{.3cm} \begin{array} {lcl} a & = & \displaystyle \frac{25-30c}{3} \\ & & \\ b & = & \displaystyle \frac{11-30c}{30} \\ \end{array} \)
Sustituyendo en la tercera ecuación:
\( 122=15 \left( \displaystyle \frac{25-30c}{3} \right)+15\left(\displaystyle \frac{11-30c}{30}\right)+261c \Rightarrow c=-0.08 854 \)
Obteniendo los siguientes valores para a y b
\( a=\displaystyle \frac{25-30×(-0.08 854)}{3}=9.2188 \hspace{.3cm} ; \hspace{.3cm} b= \displaystyle \frac{11-30×(-0.08 854)}{30}=0.45521 \)La ecuación de la parábola ajustada en función de \( x^′ \) es:
\( y=9.2188+0.45521x^′-0.08 854x^{′2} \)
y en función de la variable \( x \) es:
\( y=9.2188+0.45521(x-6)-0.08 854(x-6)^2=3.3+1.5177x-0.0854x^2 \)
Hipérbola equilátera
Suponemos que la curva que mejor se ajusta a la nube de puntos es de tipo hiperbólico, de ecuación
\( y=a+ \displaystyle \frac{b}{x} \hspace{.3cm} ; \hspace{.3cm} a,b∈R \)
Realizando la siguiente transformación
\( z= \displaystyle \frac{1}{x} \hspace{.2cm} \Rightarrow \hspace{.2cm} y=a+bz, \)
la ecuación de la hipérbola equilátera se transforma en una recta cuyo ajuste por mínimos cuadrados se realiza.
Ejemplo 3.4: Se dispone de la siguiente información referente a 6 familias sobre el gasto en espectáculos (Y) y la renta disponible mensual (X)
\( \begin{array} {|l|c|c|c|c|c|c|} \hline y_{i} & 3 & 5 & 6 & 9 & 10 & 14 \\ \hline x_{i} & 60 & 70 & 80 & 100 & 150 & 210 \\ \hline \end{array} \)
Estimar los parámetros de la función: \(y=a+b/x \).
Respuesta:
Realizamos el cambio de variable \( z=1/x \). Por lo tanto, el problema se reduce a ajustar la recta: \( y=a+bz \)
\( \begin{array} {|c|c|c|c|c|c|} \hline x_{i} & y_{i} & z_{i}= \displaystyle \frac{1}{x_{i}} & z_{i}^2 & z_{i}y_{i} & y_{i}^2 \\ \hline 60 & 3 & 0.0167 & 2.789×10^{-4} & 0.0501 & 9 \\ \hline 70 & 5 & 0.0143 & 2.044×10^{-4} & 0.0715 & 25 \\ \hline 80 & 6 & 0.0125 & 1.562×10^{-4} & 0.075 & 36 \\ \hline 100 & 9 & 0.0100 & 1×10^{-4} & 0.09 & 81 \\ \hline 150 & 10 & 0.0067 & 4.489×10^{-5} & 0.067 & 100 \\ \hline 210 & 14 & 0.0047 & 2.209×10^{-5} & 0.0658 & 196 \\ \hline & 47 & 0.0649 & 8.066×10^{-4} & 0.4194 & 447 \\ \hline \end{array} \)
\( y= \displaystyle \frac{47}{6} \hspace{.3cm} ; \hspace{.3cm} z= \displaystyle \frac{0.0649}{6} \hspace{.3cm} ; \hspace{.3cm}σ_{z}^2= \displaystyle \frac{8.066×10⁻⁴}{6}- \left( \displaystyle \frac{0.0649}{6} \right)^2=1.75×10⁻5 \)
\( σ_{yz}=\displaystyle \frac{0.4194}{6}- \displaystyle \frac{47}{6}× \displaystyle \frac{0.0649}{6}=-0.0148 \)
Recta de regresión \( Y/Z: \hspace{.3cm} y-\bar{y}= \displaystyle \frac{σ_{yz}}{σ_{z}^2}(z-\bar{z} ) \)
\( y- \displaystyle \frac{47}{6}= \displaystyle \frac{-0.0148}{1.74×10^-5} \left( z- \displaystyle \frac{0.0649}{6} \right) \hspace{.2cm} \Rightarrow \hspace{.2cm} y=17.03- \displaystyle \frac{850.57}{x} \)
Función potencial
Supongamos que la curva que mejor se ajusta a la nube de puntos tiene de ecuación
\( y=ax^{b}\hspace{.3cm} ; \hspace{.3cm} a,b \in R \hspace{.3cm} [2] \)
En este tipo de funciones, antes de aplicar el método de mínimos cuadrados, hay que linealizar y para ello se toman logaritmos neperianos o decimales en la ecuación ([2])
\( y=ax^{b} \hspace{.2cm} \Rightarrow \hspace{.2cm} \ln y= \ln a+b \ln x \hspace{.2cm} \Rightarrow \hspace{.2cm} y^′=a^′+bx^′ \)
con \( y^′= \ln y \hspace{.3cm} ; \hspace{.3cm} a^′= \ln a \hspace{.3cm} ; \hspace{.3cm} x^′= \ln x \) hemos reducido el problema a ajustar una recta.
Ejemplo 3.5: Estudiando el mercado de un cierto producto de consumo se ha reunido la siguiente información sobre los consumidores
\( \begin{array} {|l|c|c|c|c|} \hline y & 1.5 & 2 & 2.5 & 3 \\ \hline x & 4 & 4.3 & 4.6 & 5 \\ \hline \end{array} \)
Ajusta una función de consumo \( y=ax^{b} \)
Respuesta:
La función \( y=ax^{b} \) se linealiza tomando logaritmos. (Utilizamos logaritmos decimales)
\( \log y= \log a+b \log x \hspace{.3cm} \) llamando \( \Rightarrow \hspace{.2cm} \) \( \begin{array} {lcd} y^′ & = & \log y \\ a^′ & = & \log a \\ x^′ & = & \log x \\ \end{array} \) \( \hspace{.3cm}\Rightarrow \hspace{.2cm} y^′=a^′+bx^′ \)
\( \begin{array} {|c|c|c|c|c|c|} \hline x_{i} & y_{i} & x_{i}^′= \log x_{i} & y_{i}^′ \log y_{i} & x_{i}^′y_{i}^′ & x_{i}^{′2} \\ \hline 4 & 1.5 & 0.60205 & 0.17609 & 0.10601 & 0.36247 \\ \hline 4.3 & 2 & 0.63346 & 0.30102 & 0.19069 & 0.40127 \\ \hline 4.6 & 2.5 & 0.66275 & 0.39794 & 0.26373 & 0.43924 \\ \hline 5 & 3 & 0.69897 & 0.47712 & 0.33349 & 0.48853 \\ \hline & & 2.59723 & 1.35217 & 0.89392 & 1.69151 \\ \hline \end{array} \)
\( b= \displaystyle \frac{σ_{y^′x^′}}{σ_{x^′}^2}= \displaystyle \frac{ \displaystyle \frac{0.89392}{4}- \left(\displaystyle \frac{1.35217}{4} \right) \left( \displaystyle \frac{2.59723}{4}\right) }{ \displaystyle \frac{1.69151}{4}- \left( \displaystyle \frac{2.59723}{4} \right)^2}= \displaystyle \frac{3.986×10^{-3}}{1.2772×10^{-3}}=3.1208 \)\( a^′=y^′-bx^′= \displaystyle \frac{1.35217}{4}-3.1208× \displaystyle \frac{2.59723}{4}=-1.6883 \hspace{.2cm}\Rightarrow \hspace{.2cm} a^′=\log a=-1.6883 \hspace{.2cm}\Rightarrow \hspace{.2cm} a=10^{-1.6883}=0.2049 \)
Por lo tanto, la función pedida tiene de ecuación: \( y=0.2049 x^{3.1208}\)
Función exponencial
Supongamos que la curva que se quiere ajustar a los datos es del tipo exponencial
\( y=ab^{x}\hspace{.3cm}; \hspace{.3cm}a,b\in R \)
Como en el caso anterior tenemos que linealizarla para que posteriormente ajustar, por mínimos cuadrados, la recta resultante
\( y=ab^{x}\hspace{.2cm}\Rightarrow \hspace{.2cm} \ln y=\ln a+x \ln b \hspace{.2cm}\Rightarrow \hspace{.2cm}\) llamando \( \hspace{.2cm} \begin{array} {lcd} y^′ & = & \ln y \\ a^′ & = & \ln a \\ b^′ & = & \ln b \\ \end{array} \) \( \hspace{.2cm}\Rightarrow \hspace{.2cm} y^′=a^′+b^′x \)
Ejemplo 3.6: Dada la siguiente distribución:
\( \begin{array} {|c|c|c|c|c|c|} \hline x_{i} & 1 & 2 & 3 & 4 & 5 \\ \hline y_{i} & 100 & 120 & 110 & 150 & 130 \\ \hline \end{array} \)
Ajustar una función exponencial del tipo \( y=ab^{x } \) ¿Es mejor dicho ajuste que si ajustamos la recta de regresión de Y/X ?
Respuesta
La función \( y=ab^{x } \) se linealiza tomando logaritmos. (Utilizamos logaritmos neperianos)
\( \ln y= \ln a+x \ln b \hspace{.2cm}\Rightarrow \hspace{.2cm} \) llamando \( \hspace{.2cm} \begin{array} {lcd} y^′ & = & \ln y \\ a^′ & = & \ln a \\
b^′ & = & \ln b \\ \end{array} \) \( \hspace{.2cm}\Rightarrow \hspace{.2cm} y^′=a^′+b^′x \)
\( \begin{array} {|c|c|c|c|c|c|c|} \hline x_{i} & y_{i} & y_{i}^′= \ln y_{i} & x_{i}y_{i}^′ & x_{i}y_{i} & y_{i}^2 & x_{i}^2 \\ \hline 1 & 100 & 4.6052 & 4.6052 & 100 & 10000 & 1 \\ \hline 2 & 120 & 4.7875 & 9.5750 & 240 & 14400 & 4 \\ \hline 3 & 110 & 4.7005 & 14.1015& 330& 1210 & 9 \\ \hline 4 & 150 & 5.0106 & 20.0424 & 600 & 22500 & 16 \\ \hline 5 & 130 & 4.8675 & 24.3375 & 650 & 16900 & 25 \\ \hline 15 & 610 & 23.9713 & 72.6616 & 1920 & 75900 & 55 \\ \hline \end{array} \)
\( \begin{array} {l} b^′= \displaystyle \frac{σ_{y^′x}}{σ_{x}^2}= \displaystyle \frac{ \displaystyle \frac{72.6616}{5}- \displaystyle \frac{15}{5}× \displaystyle \frac{23.9713}{5}} {\displaystyle \frac{55}{5}- \left( \displaystyle \frac{15}{5} \right)^2 }= \displaystyle \frac{0.14954}{2}=0.07477 \\ & \\ a^′= \bar{y}^′-b^′ \bar{x}= \displaystyle \frac{ 23.9713}{5}-0.07477× \displaystyle \frac{15}{5}=4.56995 \\ \end{array} \)
\( \Rightarrow \begin{array} {l} b^′= \ln b=0.07477 \Rightarrow b=e^{0.07477}=1.0776 \\ a^′= \ln a=4.56995 \Rightarrow a=e^{4.56995}=96.54 \\ \end{array} \)
Por lo tanto la función pedida tiene de ecuación
\( y=96.54×(1.0776)^{x} \)
Realizamos el ajuste por medio de la recta de regresión \( Y/X: y=a+bx \Rightarrow \)
\( \begin{array} {l} b= \displaystyle \frac{σ_{yx}}{σ_{x}^2}= \displaystyle \frac{ \displaystyle \frac{1920}{5}- \displaystyle \frac{15}{5}× \displaystyle \frac{610}{5} }{\displaystyle \frac{55}{5}- \left(\displaystyle \frac{15}{5} \right)^2 }= \displaystyle \frac{18}{2}=9 \\ & \\ a=\bar{y}-b \bar{x}= \displaystyle \frac{610}{5}-9× \displaystyle \frac{15}{5}=95 \\ \end{array} \) \( \Rightarrow y=95+9x \)
Para comparar los dos ajustes realizados, necesitamos la varianza residual de cada uno de ellos
- Varianza residual de la recta \( Y/X: y=95+9x \)
\( V_{r}(y)=V(y)(1-r^2) \)
\( \begin{array} {l} V(y)= \displaystyle \frac{75900}{5}- \left( \displaystyle \frac{610}{5} \right)^2=296 \\ r^2= \displaystyle \frac{σ_{xy}^2}{σ_{x}^2 σ_{y}^2}= \displaystyle \frac{18^2}{2×296}=0.547 \\ \end{array} \) \( \Rightarrow V_{r}(y)=134.088 \)
- Varianza residual de la función exponencial: \( y=96.54×(1.0776)^{x} \)
\( V_{r}(y)= \displaystyle \frac{1}{n}\sum_{i=1}^5(y_{i}-\hat{y}_{i})^2n_{i} \hspace{.3cm} \) ,
donde \( \hat{y}_{i}=ab^{x_{i}} \Rightarrow \ln \hat{y}_{i}= \ln a +x_{i} \ln b=4.56995+0.07477x_{i} \)
\( \begin{array} {|c|c|c|c|c|} \hline x_{i} & y_{i} &\ln y_{i}=4.56995+0.07477x_{i} & y_{i} & (y_{i}-y_{i})^2 \\ \hline 1 & 100 & 4.64472 & 104.035 & 16.28 \\ \hline 2 & 120 & 4.71949 & 112.111 & 62.23 \\ \hline 3 & 110 & 4.79426 & 120.814 & 116.94 \\ \hline 4 & 150 & 4.86903 & 130.194 & 392.25 \\ \hline 5 & 130 & 4.9438 & 140.302 & 106.14 \\ \hline 15 & 610 & & & 693.85 \\ \hline \end{array} \)
Por lo tanto: \( V_{r}(y)= \displaystyle \frac{1}{n}\sum_{i=1}^5 (y_{i}-\hat{y}_{i})^2= \displaystyle \frac{693.85}{5}=138.77\)
Es mejor ajuste el de la recta de regresión ya que la varianza residual es menor.
Ejercicios propuestos: Relación III
1. Dadas las distribuciones bidimensionales siguientes, contestar a cada una de las cuestiones planteadas:
\( \begin{array} {|c|c|c|c|} \hline X/Y & 10 & 15 & 20 \\ \hline 1 & 0 & 2 & 0 \\ \hline 2 & 1 & 0 & 0 \\ \hline 3 & 0 & 0 & 3 \\ \hline 4 & 0 & 1 & 0 \\ \hline \end{array} \) \( \hspace{.2cm} \begin{array} {|c|c|c|c|} \hline X/Y & 10 & 15 & 20 \\ \hline 1 & 0 & 2 & 0 \\ \hline 2 & 1 & 0 & 0 \\ \hline 3 & 0 & 0 & 3 \\ \hline \end{array} \) \( \hspace{.2cm} \begin{array} {|c|c|c|c|} \hline X/Y & 10 & 15 & 20 & 25 \\ \hline 1 & 0 & 3 & 0 & 1 \\ \hline 2 & 0 & 0 & 1 & 0 \\ \hline 3 & 2 & 0 & 0 & 0 \\ \hline \end{array} \)
¿Depende funcionalmente?
a) X de Y (Sol: 1ª tabla: No; 2ª tabla: Si; 3ª tabla: Si)
b) Y de X (Sol: 1ª tabla: Si; 2ª tabla: Si; 3ª tabla: No)
2. Una factoría de una marca de refrescos ha tomado al azar 10 semanas al año, observando la temperatura media correspondiente a cada una de ellas y la cantidad de refrescos pedidos durante cada uno de dichos periodos. La información obtenida es:
\( \begin{array} {|l|c|c|c|c|c|c|c|c|c|c|} \hline Temperatura \hspace{.2cm} media & 10 & 28 & 12 & 31 & 30 & 19 & 24 & 5 & 9 & 15 \\ \hline N^{o} \hspace{.2cm} de \hspace{.2cm} refrescos & 21 & 65 & 19 & 72 & 75 & 39 & 67 & 11 & 12 & 24 \\ \hline \end{array} \)
¿Puede la factoría planificar la cantidad de producción de la temperatura esperada? ¿De qué forma? (Sol: \( y=-9.33+2.723x \hspace{.2cm} ; \hspace{.2cm} r^2=0.95347 \) (Es suficientemente alto)).
3. Se realiza un experimento para estudiar la relación entre el periodo de incubación (número de días desde que se pusieron los huevos) y la media del tiempo de incubación (número medio de minutos dedicados ininterrumpidamente a la incubación en el nido) en un ave marina: el charrán de pico de gaviota. Se pretende obtener una ecuación mediante la cual se pueda predecir el tiempo medio de incubación (Y) a partir del conocimiento del periodo de incubación (X). Utilizando fotografías a intervalos de tiempo se obtuvieron los siguientes datos. Se pide:
\( \begin{array} {|l|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline X & 0.25 & 0.50 & 1 & 1.5 & 2 & 2.5 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 10 \\ \hline Y & 30 & 18 & 22 & 40 & 19 & 10 & 55 & 23 & 18 & 26 & 21 & 52 & 62 & 45 & 87 \\ \hline \end{array} \)
a) Calcular la recta de regresión que predice el valor de Y a partir del conocimiento de X (Sol: \( y=17.357+3.837x \))
b) ¿Existe una relación lineal importante entre las variables? (Sol: r=0.63 (relación moderadamente fuerte entre las variables)).
4. Se realiza un estudio para investigar la relación entre el nivel de humedad del suelo y la tasa de mortalidad en lombrices. La tasa de mortalidad, Y, es la proporción de lombrices de tierra que mueren tras un periodo de dos semanas; el nivel de humedad, X, viene medido en milímetros de agua por centímetro cuadrado de suelo. Los datos se muestran en la siguiente tabla. Se pide:
\( \begin{array} {|l|c|c|c|c|c|c|c|c|c|c|c|} \hline X & 0.31 & 0.31 & 0.56 & 0.56 & 0.89 & 0.89 & 0.96 & 0.96 & 1.15 & 1.15 & 1.25 \\ \hline Y & 0.2 & 0.1 & 0 & 0.2 & 0.3 & 0.5 & 0 & 0.6 & 0.4 & 0.2 & 0.5 \\ \hline \end{array} \)
a) ¿Muestran los datos una tendencia lineal? (Sol: \( y=0.0097+0.3217x \hspace{.2cm} ; \hspace{.2cm} r=0.521 \) (relación moderadamente fuerte entre las variables))
b) Determinar el grado de asociación lineal entre la tasa de mortalidad y el nivel de humedad y la bondad del ajuste realizado en la recta de regresión. (Sol: \( r^2=0.2716 \) (el modelo explica un 27.16% de la variabilidad de la tasa de mortalidad)).
5. Se realiza un estudio para establecer una ecuación mediante la cual se pueda utilizar la concentración de estrona en la saliva, X, para predecir la concentración del esteroide en plasma libre, Y. Se extrajeron los siguientes datos a 13 individuos sanos. Se pide:
\( \begin{array} {|l|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline X & 7.4 & 7.5 & 8 & 9 & 9.5 & 10 & 11 & 12.5 & 13 & 14 & 15.5 & 16 & 17 \\ \hline Y & 25 & 29.5 & 32 & 33.5 & 36 & 42 & 43.5 & 56 & 52.5 & 62 & 61 & 63.5 & 64 \\ \hline \end{array} \)
a) Estudiar la posible relación lineal entre ambas variables, obteniendo su grado de ajuste. (Sol: \( y=-1.9824+4.1640x \hspace{.2cm} ; \hspace{.2cm} r^2=0.9501 \) )
b) Utilizar la línea de regresión estimada para predecir el nivel de estrona en plasma libre de un individuo cuyo nivel de estrona en saliva es de 17.5. (Sol:y=70.88).
6. La siguiente tabla muestra la edad (X) y la presión sanguínea (Y) de 10 mujeres:
\( \begin{array} {|l|c|c|c|c|c|c|c|c|c|c|} \hline Edad & 56 & 42 & 72 & 36 & 63 & 47 & 55 & 47 & 38 & 42 \\ \hline Presión & 148 & 126 & 159 118 & 149 & 130 & 151 & 142 & 114 & 141 \\ \hline \end{array} \)
Dar una predicción lineal para la presión sanguínea de una mujer de 51 años. (Sol: \( y=80.444+1.1517x \hspace{.2cm} ; \hspace{.2cm} 139.18 \)).
7. Elegidos 50 matrimonios al azar y preguntadas la edad de ambos al contraer matrimonio se obtuvo la siguiente tabla:
\( \begin{array} {|l|c|c|c|c|c|} \hline X/Y & 15-20 & 20-25 & 25-30 & 30-35 & 35-40 \\ \hline 15-18 & 3 & 2 & 3 & 0 & 0 \\ \hline 18-21 & 0 & 4 & 2 & 2 & 0 \\ \hline 21-24 & 0 & 7 & 10 & 6 & 1 \\ \hline 24-27 & 0 & 0 & 2 & 5 & 3 \\ \hline \end{array} \)
donde X es la edad de la mujer e Y la edad del hombre. Obtener:
a) Recta de regresión de Y/X y de X/Y y el coeficiente de correlación lineal. (Sol: \( y=4.54+1.06x \hspace{.2cm} ; \hspace{.2cm} x=12.54+0.3289y \hspace{.2cm} ; \hspace{.2cm} r=0.593 \))
b) Preguntada una mujer dijo que se casó con 22 años ¿Qué edad podemos aventurar que tenía el marido al casarse? Preguntado un hombre dijo que se casó con 24 años ¿Qué edad tendría su esposa al casarse? (Sol: 28; 20).
8. Dos variables tienen las siguientes rectas de regresión mínimo-cuadráticas:
\( 8x+2y=1 \hspace{.2cm} ; \hspace{.2cm} 16x+9y-1=0 \)
Calcular x, y y el coeficiente de correlación lineal. (Sol: 0.175; -0.2; r=-0.666).
9. Partiendo de una muestra de 200 pares de observaciones se calcularon las siguientes cantidades:
\(\sum_{i}x_{i}=11.34 \hspace{.2cm} ; \hspace{.2cm}\sum_{i}x_{i}^2=12.16 \hspace{.2cm} ; \hspace{.2cm}\sum_{i}x_{i}y_{i}=22.13 \hspace{.2cm} ; \hspace{.2cm}\sum_{i}y_{i}=20.72;\sum_{i}y_{i}^2=84.96 \)
Se pide:
a) Calcular las dos rectas de regresión y dibujarlas (Sol: \( y=7.28×10^{-4}+1.824x \hspace{.2cm} ; \hspace{.2cm} x=0.0147+0.258y \))
b) ¿Son fiables las predicciones efectuadas con las rectas anteriores? (Sol: \( r^2=0.4697 \) (Si es fiable)).
10. En una determinada zona oceánica, se ha realizado un estudio sobre el comportamiento del mar, en relación a diversos factores entre los cuales se encuentra la velocidad del viento. A lo largo de 20 días y durante el último periodo de tiempo se ha observado conjuntamente la velocidad del viento (X) y la altura de las olas (Y). La información obtenida se dispone en la siguiente tabla. Se pide:
\( \begin{array} {|l|c|c|c|c|} \hline X/Y & <0.2 & 0.2-1 & 1-3 & 3-7 \\ \hline <2 & 2 & 0 & 0 & 0 \\ \hline 2-8 & 0 & 5 & 1 & 0 \\ \hline 8-12 & 0 & 0 & 4 & 1 \\ \hline 12-20 & 0 & 0 & 2 & 5 \\ \hline \end{array} \)
a) Calcular la recta de regresión de Y/X (Sol: \( y=-0.4239+0.2870x \))
b) ¿Qué valor asignará a la variable y si dispusiera de un valor x=8.3? ¿Es adecuada tal asignación? (Sol:\( y=1.95820 \hspace{.2cm} ; \hspace{.2cm} r^2=0.6798 \) (Buen ajuste)).
11. En un cierto estudio sobre fiabilidad se han obtenido los datos de la siguiente tabla:
\( \begin{array} {|l|c|c|c|c|c|c|c|} \hline X/Y & <3 & 3-4 & 4-5 & 5-6 & 6-7 & 7-8 & >8 \\ \hline <5 & 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline
15-20 & 0 & 8 & 0 & 0 & 0 & 0 & 0 \\ \hline 20-25 & 0 & 0 & 9 & 1 & 0 & 0 & 0 \\ \hline 25-30 & 0 & 0 & 0 & 9 & 0 & 0 & 0 \\ \hline
30-35 & 0 & 0 & 0 & 0 & 9 & 0 & 0 \\ \hline 35-40 & 0 & 0 & 0 & 0 & 0 & 7 & 1 \\ \hline >40 & 0 & 0 & 0 & 0 & 0 & 0 & 3 \\ \hline \end{array} \)
a) Calcular el coeficiente de correlación lineal. (Sol: 0.9695)
b) Obtener las rectas de regresión de Y/X y de X/Y. (Sol: \( y=0.9747+0.1696x \hspace{.2cm} ; \hspace{.2cm} x=-3.76+5.5376y \)).
12. Cinco niños de 2, 4, 6, 7 y 8 años pesan respectivamente, 15, 19, 25, 33 y 34 Kgs. Hallar la recta de regresión mínimo cuadrática del peso con respecto a la edad. (Sol: \( y=6.9+3.388x \hspace{.2cm} ; \hspace{.2cm} r^2=0.948 \) (Buen ajuste)).
13. La siguiente tabla muestra el número de calzado y los pesos de 55 estudiantes:
\( \begin{array} {|l|c|c|c|c|c|c|c|} \hline X/Y & 50 & 60 & 65 & 70 & 75 & 80 & 85 \\ \hline 39 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 40 & 0 & 3 & 3 & 4 & 0 & 0 & 0 \\ \hline 41 & 0 & 3 & 4 & 6 & 0 & 0 & 1 \\ \hline 42 & 0 & 0 & 8 & 8 & 7 & 2 & 0 \\ \hline 43 & 0 & 0 & 2 & 0 & 1 & 0 & 0 \\ \hline 44 & 0 & 0 & 0 & 0 & 0 & 0 & 2 \\ \hline \end{array} \)
Dar una predicción del peso de un estudiante que calza el 38 ¿Es buena la predicción? (Sol: \( y=-80.15+3.59576x \hspace{.2cm} ; \hspace{.2cm} y=56.48 \hspace{.2cm} ; \hspace{.2cm} r^2=0.3060 \)).
Autora: Ana María Lara Porras. Universidad de Granada
Estadística para Biología y Ciencias Ambientales. Tratamiento informático mediante SPSS. Proyecto Sur Ediciones.