ESTADÍSTICA DESCRIPTIVA: REPRESENTACIONES GRÁFICAS
Objetivos
- Resumir, ordenar y analizar conjuntos de datos
- Calcular diversas características de una variable estadística univariante
- Representar gráficamente la distribución de frecuencias
- Realizar análisis exploratorio de datos.
Introducción al Análisis Descriptivo
En esta práctica tomaremos un primer contacto con las técnicas estadísticas que se utilizan para ordenar, analizar y representar un conjunto de datos, con el fin de describir apropiadamente sus características. El primer paso en el análisis de datos, una vez introducidos los mismos, es realizar un análisis descriptivo o análisis exploratorio de datos. Los principales objetivos de un análisis descriptivo o análisis exploratorio de datos son la descripción y la síntesis de los datos. Para ello, los datos se organizan en tablas, se calculan medidas que describen sus características más importantes y se realizan representaciones gráficas.
Este análisis inicial proporciona una idea de la forma que tiene la distribución de las observaciones y permite obtener estadísticos de tendencia central (media, mediana y moda), de dispersión (varianza, desviación típica, rango), de forma (asimetría, curtosis), de posición (percentiles), así como gráficos de barras, de sectores e histograma.
R dispone de un amplio conjunto de herramientas para el análisis descriptivo de un conjunto de datos.
Tabla de Frecuencias
Para crear tablas de frecuencia en R se emplea la función table o la función prop.table, dependiendo de si la tabla muestra las frecuencias absolutas o las frecuencias relativas. La sintaxis de estas órdenes es la siguiente:
> table(x) # para frecuencias absolutas
> prop.table(tab) # para las frecuencias relativas
La principal diferencia entre las dos funciones reside en el tipo de los argumentos que necesita cada una.
- table construye la tabla de frecuencias absolutas a partir de la variable que recibe como argumento
- prop.table recibe como argumento una tabla o una matriz que representa una tabla de frecuencias absolutas, y a partir de ella construye la tabla de frecuencias relativas asociada. Es decir, prop.table recibe como argumento el resultado que devuelve la función table.
Ejemplo1:
En la siguiente tabla se recogen 29 datos sobre el peso, altura, velocidad y color
\( \begin{array} {|c|c|c|c|} \hline peso & altura & velocidad & color \\ \hline 7.2 & 50 & 10.3 & Blanco \\ \hline 8.5 & 66 & 10.3 & Amarillo \\ \hline 9.8 & 73 & 10.2 & Verde \\ \hline 6.5 & 72 & 16.4 & Verde \\ \hline 7.5 & 81 & 18.8 & Verde \\ \hline 10.1 & 73 & 19.7 & Verde \\ \hline 11 & 66 & 15.6 & Blanco \\ \hline 11 & 75 & 21.2 & Amarillo \\ \hline 11.1 & 70 & 22.6 & NA \\ \hline 11.2 & 75 & 19.9 & Blanco \\ \hline 11.3 & 69 & 24.2 & Amarillo \\ \hline 11.4 & 76 & 21 & Blanco \\ \hline 11.4 & 76 & 21.4 & Verde \\ \hline 11.7 & 69 & 21.3 & Verde \\ \hline 12 & 75 & NA & Amarillo \\ \hline 12.9 & 64 & 22.2 & Amarillo \\ \hline 12.9 & 55 & 33.8 & Blanco \\ \hline 10.3 & 76 & 27.4 & Amarillo \\ \hline 9.7 & 71 & 25.7 & Verde \\ \hline 10.8 & 64 & 24.9 & Verde \\ \hline 11 & 78 & 23.1 & Amarillo \\ \hline 10.2 & 70 & 31.7 & Amarillo \\ \hline 10.5 & 74 & 36.3 & Verde \\ \hline 6.5 & 72 & 38.3 & Verde \\ \hline 6.3 & 77 & 42.6 & Verde \\ \hline 7.3 & 51 & 55.4 & Blanco \\ \hline 7.5 & 62 & NA & Blanco \\ \hline 7.9 & 60 & 58.3 & Amarillo \\ \hline 8.2 & 70 & NA & Verde \\ \hline \end{array} \)
Nota: Se puede realizar: a) en la Consola de R y b) En el editor de R
a) En la Consola de R, como lo hacemos a continuación
> datos <- read.table(“C:/Users/Usuario/Desktop/misdatos.txt”, header = TRUE)
o bien
> setwd(“C:/Datos”) # situarse en el directorio de trabajo
> datos <- read.table(“misdatos.txt”, header = TRUE)
> datos
peso altura velocidad color
1 7.2 50 10.3 Blanco
2 8.5 66 10.3 Amarillo
3 9.8 73 10.2 Verde
4 6.5 72 16.4 Verde
5 7.5 81 18.8 Verde
6 10.1 73 19.7 Verde
7 11.0 66 15.6 Blanco
8 11.0 75 21.2 Amarillo
9 11.1 70 22.6 <NA>
10 11.2 75 19.9 Blanco
11 11.3 69 24.2 Amarillo
12 11.4 76 21.0 Blanco
13 11.4 76 21.4 Verde
14 11.7 69 21.3 Verde
15 12.0 75 NA Amarillo
16 12.9 64 22.2 Amarillo
17 12.9 55 33.8 Blanco
18 10.3 76 27.4 Amarillo
19 9.7 71 25.7 Verde
20 10.8 64 24.9 Verde
21 11.0 78 23.1 Amarillo
22 10.2 70 31.7 Amarillo
23 10.5 74 36.3 Verde
24 6.5 72 38.3 Verde
25 6.3 77 42.6 Verde
26 7.3 51 55.4 Blanco
27 7.5 62 NA Blanco
28 7.9 60 58.3 Amarillo
29 8.2 70 NA Verde
b) En el Editor de R. Para ello primero abrimos un nuevo script: Elegimos en el menú principal: Archivo/Nuevo script y escribimos
datos <- read.table(“misdatos.txt”, header = TRUE) # Se recomienda situarse en el directorio donde están los archivos de los datos
datos
Figura 1: Consola de R y Editor de datos de R
Señalizamos todo en el Editor de R y pulsamos las teclas Ctrl +R para ejecutarlo. Mostrándose lo siguiente en la Consola de R
> datos <- read.table(“misdatos.txt”, header = TRUE)
> datos
peso altura velocidad color
1 7.2 50 10.3 Blanco
2 8.5 66 10.3 Amarillo
3 9.8 73 10.2 Verde
4 6.5 72 16.4 Verde
5 7.5 81 18.8 Verde
6 10.1 73 19.7 Verde
7 11.0 66 15.6 Blanco
8 11.0 75 21.2 Amarillo
9 11.1 70 22.6 <NA>
10 11.2 75 19.9 Blanco
11 11.3 69 24.2 Amarillo
12 11.4 76 21.0 Blanco
13 11.4 76 21.4 Verde
14 11.7 69 21.3 Verde
15 12.0 75 NA Amarillo
16 12.9 64 22.2 Amarillo
17 12.9 55 33.8 Blanco
18 10.3 76 27.4 Amarillo
19 9.7 71 25.7 Verde
20 10.8 64 24.9 Verde
21 11.0 78 23.1 Amarillo
22 10.2 70 31.7 Amarillo
23 10.5 74 36.3 Verde
24 6.5 72 38.3 Verde
25 6.3 77 42.6 Verde
26 7.3 51 55.4 Blanco
27 7.5 62 NA Blanco
28 7.9 60 58.3 Amarillo
29 8.2 70 NA Verde
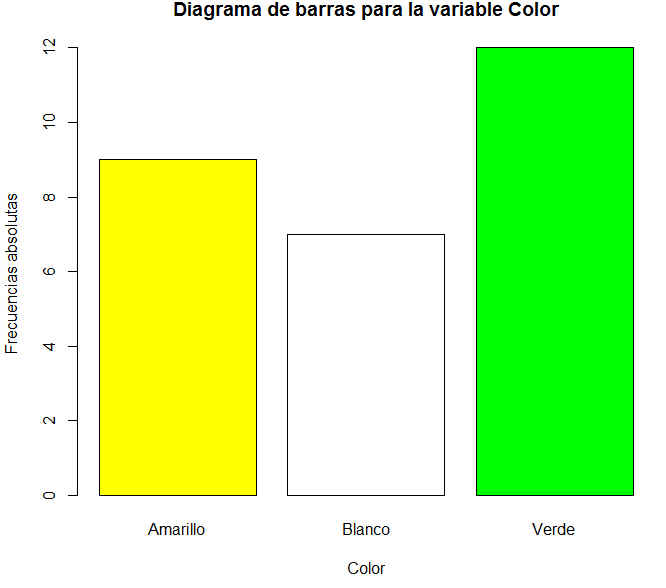
> tabla_color <- table(datos$color)
> tabla_color
Amarillo Blanco Verde
9 7 12
> prop.table(tabla_color)
Amarillo Blanco Verde
0.3214286 0.2500000 0.4285714
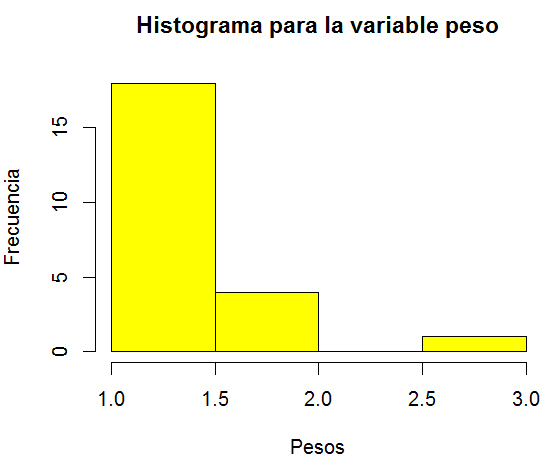
> tabla_peso <- table(datos$peso)
> tabla_peso
6.3 6.5 7.2 7.3 7.5 7.9 8.2 8.5 9.7 9.8 10.1 10.2 10.3 10.5 10.8 11 11.1 11.2 11.3 11.4 11.7 12 12.9
1 2 1 1 2 1 1 1 1 1 1 1 1 1 1 3 1 1 1 2 1 1 2
> prop.table(tabla_peso)
6.3 6.5 7.2 7.3 7.5 7.9 8.2 8.5 9.7 9.8 10.1 10.2 10.3 10.5 10.8
0.03448276 0.06896552 0.03448276 0.03448276 0.06896552 0.03448276 0.03448276 0.03448276 0.03448276 0.03448276 0.03448276 0.03448276 0.03448276 0.03448276 0.03448276
11 11.1 11.2 11.3 11.4 11.7 12 12.9
0.10344828 0.03448276 0.03448276 0.03448276 0.06896552 0.03448276 0.03448276 0.06896552
Representaciones gráficas
R ofrece una gran variedad de gráficos, el comando demo(graphics) muestra dichos gráficos. Atendiendo al tipo de datos vamos a utilizar varios tipos de gráficos.
-
- Variables cualitativas o variables cuantitativas de tipo discreto: Se pueden considerar gráficos de sectores o gráficos de barras, los cuales se obtienen en R mediante las funciones pie y barplot, respectivamente. Los argumentos más importantes de estas funciones son:
pie(x, labels = names(x), clockwise = FALSE, init.angle = if(clockwise) 90 else 0, col = NULL, main = NULL)
barplot(x, horiz = FALSE, col = NULL, main = NULL, sub = NULL, xlab = NULL, ylab = NULL)
donde
x es un vector con las frecuencias de las observaciones. Igualmente, puede ser una tabla de frecuencia (de las obtenidas con table o prop.table)
labels es un vector de cadenas de caracteres que indican los nombres de cada una de las categorías que aparecen en el gráfico de sectores
clockwise es un argumento lógico que indica si los sectores se dibujan en sentido horario (clockwise = TRUE) o en sentido antihorario (clockwise = FALSE, que es la opción por defecto)
init.angle es un valor numérico que indica el ángulo (en grados) en el que se sitúa el primer sector. Por defecto, el primer sector empieza a dibujarse a los 90 grados (- a las 12 en punto -, cuando clockwise es igual a TRUE) o a los 0 grados (- a las 3 en punto -, cuando clockwise es igual a FALSE)
horiz es un argumento lógico que indica si las barras del gráfico de barras se dibujan de forma vertical (horiz = FALSE, que es la opción por defecto) u horizontal (horiz = TRUE)
col es un vector en el que se indican los colores de las barras o los sectores del gráfico
main y sub son cadenas de caracteres en la que se especifican el título y el subtítulo del gráfico
xlab e ylab son cadenas de caracteres en las que se especifican los nombres de los ejes X e Y.
- Variables cuantitativas: Los gráficos que se suelen emplear con más frecuencia son el histograma, el diagrama de tallos y hojas y el diagrama de caja y bigotes. En R, se utilizan las órdenes hist, stem y boxplot para la obtención de histogramas, de diagramas de tallos y hojas y de diagramas de caja y bigotes, respectivamente. Éstas son las principales opciones de estas funciones:
hist(x, breaks = “Sturges”, right = TRUE, col = NULL, main = paste(“Histogram of” , xname))
stem(x)
boxplot(x, range = 1.5, col = NULL, main = NULL)
donde, en este caso,
x es el vector de valores de la variable a partir de los cuales se dibujará el gráfico.
breaks indica la forma en la que se calcularán los intervalos en el histograma. Las opciones disponibles para este parámetro son “Sturges” (que es la opción por defecto) “Scott” y “FD” “Freedman-Diaconis“. Para más información sobre estos métodos, así como la fórmula que emplea cada uno de ellos para determinar el número de intervalos, se puede consultar el siguiente enlace (en inglés): http://www.mas.ncl.ac.uk/~nlf8/teaching/mas1343/notes/chap4-5.pdf
range es un valor numérico que determina la extensión de los bigotes de la caja. Para un valor positivo de range, los bigotes se extienden hasta el último dato que no supere 1.5 veces la longitud de la caja (el rango intercuartílico). Para un valor de 0, los bigotes se extienden hasta el dato más lejano
right es un argumento lógico que indica si los intervalos son cerrados por la izquierda y abiertos por la derecha (en cuyo caso, right = TRUE, que es la opción por defecto) o viceversa (right = FALSE).
Las opciones col y paste funcionan igual que en los gráficos de barras y sectores.
Nota: El programa R ha abierto puertas de accesibilidad a los análisis estadísticos de las personas ciegas, mediante un paquete adicional llamado BrailleR, http://r-resources.massey.ac.nz/BrailleR. Este paquete permite que la información gráfica esté disponible en forma de texto.
http://r-resources.massey.ac.nz/BrailleR: Created and maintained by Jonathan Godfrey
Institute of Fundamental Sciences, Massey University,
Palmerston North, New Zealand)
Ejemplos:
> pie(table(datos$color), col = c(“yellow”, “white”, “green”), main = “Diagrama de sectores para la variable color”)
Se muestra el siguiente gráfico de sectores para la variable Color:
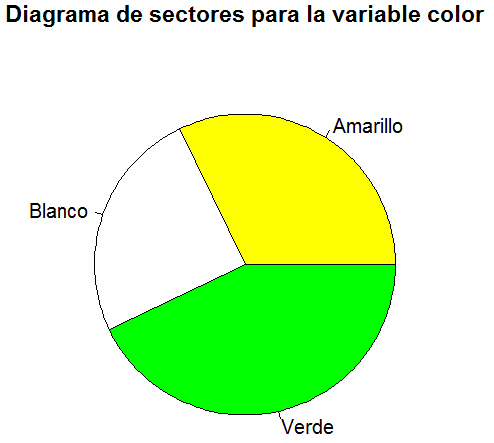 Figura 2: Diagrama de sectores
Figura 2: Diagrama de sectores
> barplot(table(datos$color), col=c(“yellow”, “white”, “green”), xlab=”Color”, ylab=”Frecuencias absolutas”,main =”Diagrama de barras para la variable Color”)
Se muestra el siguiente gráfico de barras para la variable Color:
> hist(table(datos$peso), col = “yellow”, main = “Histograma para la variable peso”, xlab=”Pesos”, ylab=”Frecuencia”)
Se muestra el siguiente histograma para la variable Peso
> stem(table(datos$altura))
The decimal point is at the |
1 | 0000000000
1 |
2 | 00000
2 |
3 | 000
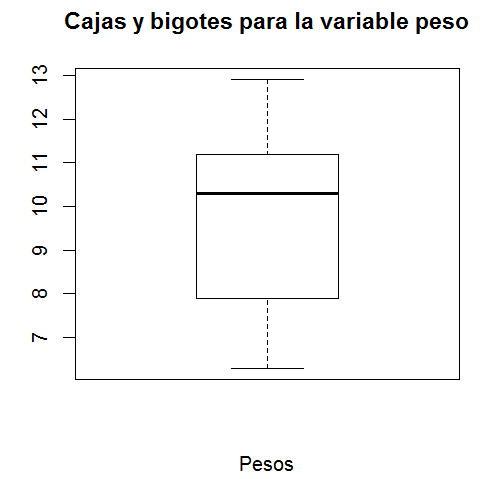
> boxplot(datos$peso, xlab=”Pesos”, main = “Cajas y bigotes para la variable peso”)
Se muestra el siguiente boxplot (Cajas y bigotes) de la variable Peso
Características o Medidas de una variable estadística
En las secciones anteriores se han planteado técnicas gráficas, tablas estadísticas y representaciones gráficas, que han proporcionado una representación visual de las variables estadísticas. Dichas técnicas gráficas nos dan una idea de la composición de la población en estudio. En esta sección vamos a resumir todos los datos recogidos en una tabla estadística en unos valores, medidas numéricas, llamadas Características o Medidas que representen o sinteticen el conjunto de datos. Son medidas que proporcionan información sobre puntos importantes de la distribución, completando la información que nos ha proporcionado las tablas estadísticas y las representaciones gráficas.
Estudiaremos las Características o medidas de posición, de dispersión, y de forma
Medidas de posición
En muchas ocasiones el interés reside en localizar el centro de la distribución (para lo cual se calculan las medidas de tendencia central), existen casos en los que los puntos que se desean estudiar distan mucho de este centro (en cuyo caso se recurre al cálculo de las medidas de tendencia no central).
Algunas de las medidas más populares dentro del grupo de medidas de tendencia central son la media, la mediana y la moda. Las funciones que calculan las dos primeras medidas en R son mean y median.
mean (x, na.rm = FALSE)
median (x, na.rm = FALSE)
donde:
x: vector con los valores de la variable
na.rm: un argumento lógico que indica si hay que eliminar los valores faltantes del conjunto de datos.
Las observaciones faltantes o no disponibles de un conjunto de datos son codificadas en R como NA (que son las iniciales de Not Available). Cuando una función de R encuentra algún NA entre los valores de las observaciones que trata de analizar devuelve como resultado NA, indicando así que los cálculos no se han podido realizar. No obstante, asignando el valor TRUE al argumento na.rm se pueden eliminar los valores faltantes y obtener así un valor para la media o la mediana, basado en las observaciones restantes.
En cuanto a la moda, R no tiene implementada ninguna función que la calcule. Pero aprovechando la potencia del programa, podemos encargarnos nosotros mismos de definir una función que calcule la moda de un conjunto de datos. Así, tendremos que copiar y pegar el siguiente código en la consola de R:
Mode <- function(x) {
ux <- unique(x)
ux[which.max(tabulate(match(x, ux)))]
}
Una vez hecho esto, podremos calcular la moda de un conjunto de datos tal y como sigue:
Mode (x)
En el caso de que existan varias modas (es decir, cuando estemos ante una distribución plurimodal), esta función mostrará únicamente la menor de ellas (o la primera en orden alfabético, si se está analizando una variable cualitativa).
Entre las medidas de posición de tendencia no central, los cuantiles figuran entre las más utilizadas. Para obtener los cuantiles de una variable en R se emplea la función quantile.
quantile(x, probs = seq(0, 1, 0.25), na.rm = FALSE)
donde:
x: vector que incluye los valores de la variable
seq: Argumento que indica los cuantiles que se van a calcular. Por defecto, se muestran los siguiente cuantiles:
- 0, que coincide con el valor mínimo
- 25, que coincide con el primer cuartil
- 50, que coincide con el segundo cuartil y con la mediana
- 75, que coincide con el tercer cuartil
- 100, que coincide con el valor máximo
na.rm: un argumento lógico que indica si hay que eliminar los valores faltantes del conjunto de datos.
El mínimo y el máximo de un conjunto de datos, además de poder calcularse como los cuantiles 0 y 100, pueden obtenerse utilizando las funciones de R min y max.
min (x, na.rm = FALSE)
max (x, na.rm = FALSE)
Medidas de dispersión
Tratan de cuantificar la variabilidad o esparcimiento de los datos informando acerca de la mayor o menor representatividad de las medidas de tendencia central.
Entre las medidas de dispersión más utilizadas se encuentran la cuasi-varianza, la cuasi-desviación típica y el rango intercuartílico, que en R se calculan a través de las funciones var, sd e IQR, respectivamente.
var(x, na.rm = FALSE)
sd(x, na.rm = FALSE)
IQR(x, na.rm = FALSE)
Los dos argumentos principales de estas funciones son x, que es el vector con los valores de la variable que se está estudiando y na.rm que, como ya se ha comentado, indica si los valores faltantes han de ser eliminados antes del análisis.
Como se ha especificado, las funciones var y sd no calculan la varianza y la desviación típica de una variable, sino su cuasi-varianza y su cuasi-desviación típica. En caso de necesitar la varianza o la desviación típica, basta con multiplicar el resultado de las funciones var y sd por (n – 1)/n, siendo n el número total de datos con el que se está trabajando.
A partir de las funciones anteriores se pueden calcular otras medidas, como el coeficiente de variación de Pearson o el rango. El coeficiente de variación se emplea para comparar la representatividad de la media entre distintas variables y se obtiene dividiendo la desviación típica de una variable entre su media. Por su parte, el rango es una medida de dispersión muy sencilla que se obtiene como la diferencia entre los valores máximo y mínimo.
Medidas de forma
Como su propio nombre indica, estas medidas se centran en el estudio de la forma que presenta una distribución a través del análisis de la simetría y la curtosis o el apuntamiento de la distribución en cuestión.
Para determinar la simetría de una distribución se emplea la función skewness, contenida en el paquete e1071. En R, un paquete no es más que un conjunto de funciones con un propósito común. Para poder utilizar las funciones incluidas en un determinado paquete, es necesario instalar el paquete y, posteriormente cargarlo.
Para instalar el paquete, utilizamos la orden install.packages(“nombre_del paquete”). En nuestro caso, tenemos que teclear
> install.packages(“e1071″) # cuidado con las comillas (tecla”)
Se muestra el CRAN mirror, donde elegimos como idioma Spain (Madrid)
Pulsamos OK, yse muestra el siguiente mensaje
— Please select a CRAN mirror for use in this session —
probando la URL ‘http://cran.es.r-project.org/bin/windows/contrib/3.2/e1071_1.6-7.zip’
Content type ‘application/zip’ length 814301 bytes (795 KB)
downloaded 795 KB
package ‘e1071’ successfully unpacked and MD5 sums checked
The downloaded binary packages are in
C:\Users\Usuario\AppData\Local\Temp\RtmpOcmE1f\downloaded_packages
Una vez que el paquete se ha instalado de forma correcta en nuestro ordenador no será necesario volver a instalarlo nunca más, siempre que no cambiemos la versión de R. Tras instalar el paquete, procederemos a cargarlo mediante la función library.
> library(“e1071”)
Warning message:
package ‘e1071’ was built under R version 3.2.2
A diferencia de la instalación, la carga de los paquetes es necesaria cada vez que se inicia una nueva sesión de R. Una vez instalado y cargado el paquete e1071, ya podemos utilizar la función skewness sin problema. Su sintaxis es:
skewness(x, na.rm = FALSE)
donde
x: es el vector que incluye los valores de la variable
na.rm: es un argumento lógico que indica si hay que eliminar los valores faltantes del conjunto de datos.
De forma análoga, para estudiar la curtosis de un conjunto de datos emplearemos la función kurtosis que también está contenida en el paquete e1071.
kurtosis(x, na.rm = FALSE)
donde los parámetros x y na.rm se definen forma similar al caso anterior.
Algunas funciones resumen
Existen funciones en R que calculan, a la vez, algunas de las medidas que se han descrito hasta ahora, summary es un buen ejemplo de este tipo de funciones, ya que cuando se aplica a una variable cuantitativa devuelve el mínimo, el máximo, la media, la mediana y los cuartiles primero y tercero de la variable. La sintaxis de esta función es la siguiente:
summary(object)
object: es el objeto (la variable en nuestro caso) del cual queremos obtener el resumen.
Ejemplos
> datos <- read.table(“C:/Users/Usuario/Desktop/misdatos.txt”, header = TRUE)
o bien
> setwd(“C:/directorio de trabajo”)
> datos <- read.table(“misdatos.txt”, header = TRUE)
> mean(datos$peso)
[1] 9.782759
> median(datos$peso)
[1] 10.3
> min(datos$peso)
[1] 6.3
> max(datos$peso)
[1] 12.9
> quantile(datos$peso, probs = c(0.25, 0.75))
25% 75%
7.9 11.2
> summary(datos$peso)
Min. 1st Qu. Median Mean 3rd Qu. Max.
6.300 7.900 10.300 9.783 11.200 12.900
> var(datos$peso, na.rm = TRUE)
[1] 3.945764
> sd(datos$peso, na.rm = TRUE)
[1] 1.986395
> IQR(datos$peso, na.rm = TRUE)
[1] 3.3
> install.packages(“e1071”) # Es necesario si aún no se ha instalado
> library(e1071)
> skewness(datos$peso)
[1] -0.3492441
> skewness(datos$peso, na.rm = TRUE)
[1] -0.3492441
> kurtosis(datos$peso, na.rm = TRUE)
[1] -1.231833
Ejercicios
Ejercicios Guiados
Ejercicio guiado
Considérese el siguiente conjunto de datos que contiene información acerca de la raza, la edad, el peso y la altura de 10 personas:
\( \begin{array} {|c|c|c|c|} \hline Raza & Edad & Peso & Altura\\ \hline Blanca & 24 & 58 & 156 \\ \hline Negra & 26 & 62 & 175 \\ \hline Blanca & 62 & 61 & 169 \\ \hline Blanca & 31 & 67 & 171 \\ \hline Negra & 30 & 71 & 159 \\ \hline Negra & 41 & 69 & 160 \\ \hline Negra & 51 & NA & 158 \\ \hline Blanca & 23 & 73 & 178 \\ \hline Blanca & 28 & 56 & 168 \\ \hline Blanca & 30 & 82 & 166 \\ \hline \end{array} \)
Tabla2. Datos del Ejercicio Guiado
a) Crea 4 variables, de manera que cada una contenga los datos de una columna. Después, crea un data frame llamado Datos con las 4 variables que acabas de crear
b) Realiza una tabla de frecuencias absolutas y otra de frecuencias relativas para la variable Raza. Almacena las tablas anteriores en dos variables y llámalas abso y rela
c) Representa la variable Raza mediante un diagrama de barras y un diagrama de sectores. Incluye un título adecuado para cada gráfico y colorea las barras y los sectores de colores diferentes
d) Para la variable Edad, realiza un histograma y un diagrama de caja y bigotes considerando la opción range = 1.5. Incluye un título apropiado para cada gráfico y colorea las barras del histograma de color verde. ¿Existe algún valor atípico en esta variable? Reduce el valor del argumento range hasta 1. ¿Varían las conclusiones?
e) Realiza un resumen de la variable Altura mediante la orden summary. Comprueba que las medidas que proporciona summary coinciden con las medidas calculadas de forma individual usando su función específica
f) Calcula el peso medio de los individuos y proporciona, al menos, dos medidas que indiquen la dispersión de esta variable
g) ¿Qué variable es más homogénea: la edad o la altura?
Ejercicio Guiado (Resuelto)
a) Crea 4 variables, de manera que cada una contenga los datos de una columna. Después, crea un data frame llamado Datos con las 4 variables que acabas de crear.
En primer lugar, se tiene que tener en cuenta el tipo de las variables, pues ello determina la manera en que hay que crearlas. En este ejemplo, la variable Raza es un factor con dos categorías mientras que el resto de variables son numéricas. De las tres variables numéricas, Peso es la única con observaciones faltantes.
> Raza <- factor(c(“Blanca”, “Negra”, “Blanca”, “Blanca”, “Negra”, “Negra”, “Negra”, “Blanca”, “Blanca”, “Blanca”), levels = c(“Blanca”, “Negra”))
> Raza
[1] Blanca Negra Blanca Blanca Negra Negra Negra Blanca Blanca Blanca
Levels: Blanca Negra
El signo + al inicio de una línea en la consola de R indica que la orden anterior no se ha terminado de escribir por completo y que continúa en esa línea.
> Edad <- c(24, 26, 62, 31, 30, 41, 51, 23, 28, 30)
> Peso <- c(58, 62, NA, 67, 71, 69, NA, 73, 56, 82)
> Altura <- c(156, 175, 169, 171, 159, 160, 158, 178, 168, 166)
Agrupamos las 4 variables en un data frame, al que vamos a llamar Datos:
> Datos <- data.frame (Raza, Edad, Peso, Altura)
Comprobemos que los datos se han guardado correctamente.
> Datos
Raza Edad Peso Altura
1 Blanca 24 58 156
2 Negra 26 62 175
3 Blanca 62 NA 169
4 Blanca 31 67 171
5 Negra 30 71 159
6 Negra 41 69 160
7 Negra 51 NA 158
8 Blanca 23 73 178
9 Blanca 28 56 168
10 Blanca 30 82 166
b) Realiza una tabla de frecuencias absolutas y otra de frecuencias relativas para la variable Raza. Almacena las tablas anteriores en dos variables y llámalas abso y rela
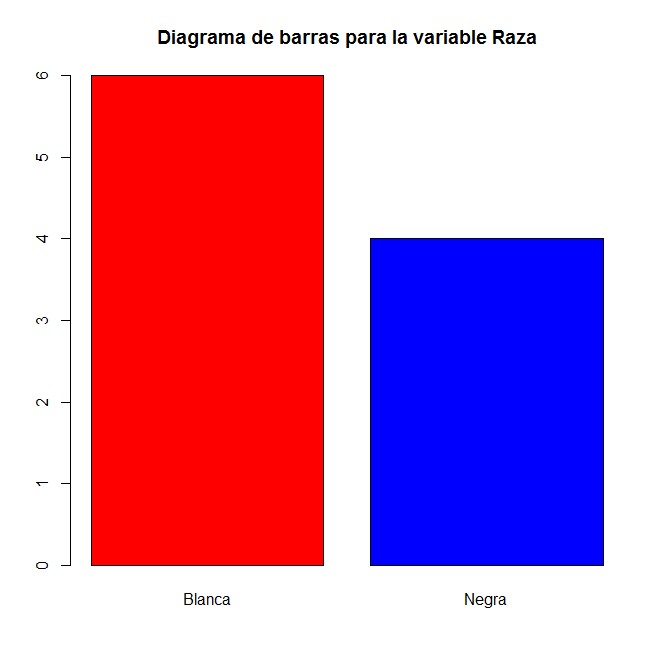
> abso <- table(Datos$Raza)
> abso
Blanca Negra
6 4
> rela <- prop.table(abso)
> rela
Blanca Negra
0.6 0.4
c) Representa la variable Raza mediante un diagrama de barras y un diagrama de sectores. Incluye un título adecuado para cada gráfico y colorea las barras y los sectores de colores diferentes
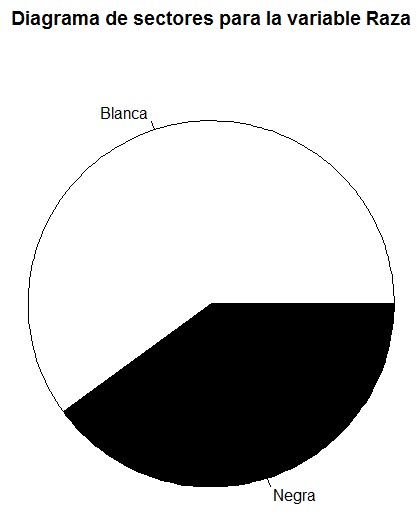
> barplot(abso, col = c(“red”, “blue”), main = “Diagrama de barras para la variable Raza”)
> pie(abso, col = c(“white”, “black”), main = “Diagrama de sectores para la variable Raza”)
d) Para la variable Edad, realiza un histograma y un diagrama de caja y bigotes considerando la opción range = 1.5. Incluye un título apropiado para cada gráfico y colorea las barras del histograma de color verde. ¿Existe algún valor atípico en esta variable? Reduce el valor del argumento range hasta 1. ¿Varían las conclusiones?
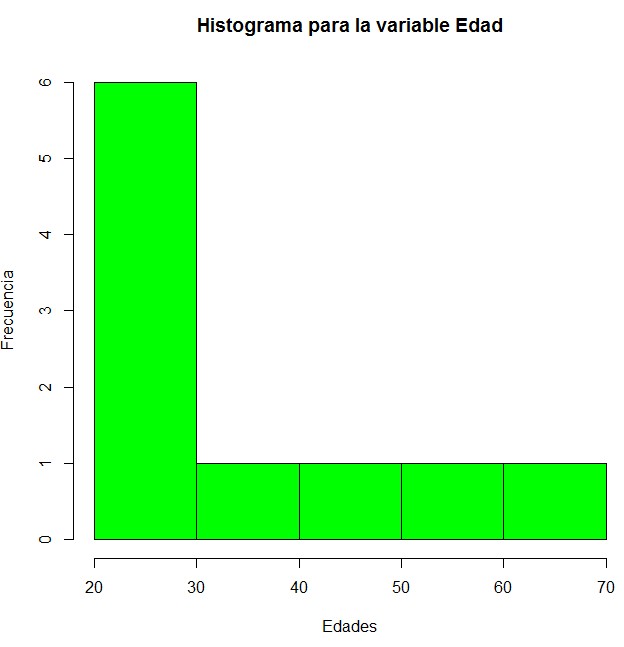
> hist(Datos$Edad, col = “green”, main = “Histograma para la variable Edad”, xlab = “Edades”, ylab = “Frecuencia”)
> boxplot(Datos$Edad, main = “Cajas y bigotes para la variable Edad (range = 1.5)”)
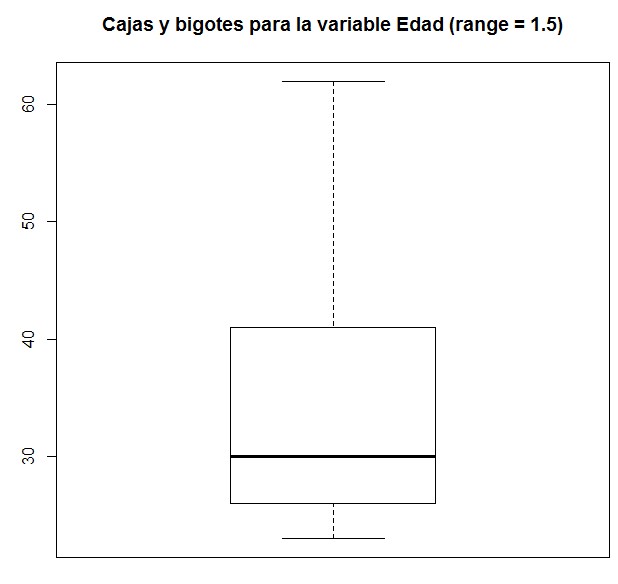 Figura 9: Caja y Bigotes (range = 1.5)
Figura 9: Caja y Bigotes (range = 1.5)
En este caso no se aprecia ningún valor atípico en el diagrama de caja y bigotes, ya que no aparece ningún valor más allá de los bigotes.
> boxplot(Datos$Edad, main = “Cajas y bigotes para la variable Edad (range = 1)”)
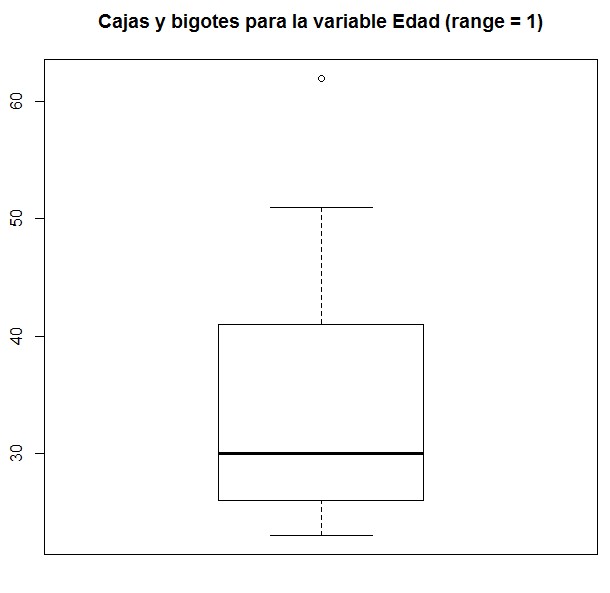 Figura 10: Caja con Bigotes (range = 1)
Figura 10: Caja con Bigotes (range = 1)
Cuando se reduce el valor de range a 1 se observa que existe un dato más allá del bigote superior, el cual se considera como atípico.
e) Realiza un resumen de la variable Altura mediante la orden summary. Comprueba que las medidas que proporciona summary coinciden con las medidas calculadas de forma individual usando su función específica
Si aplicamos la función summary a la variable Altura, obtenemos el siguiente resultado
> summary(Datos$Altura)
Min. 1st Qu. Median Mean 3rd Qu. Max.
156.0 159.2 167.0 166.0 170.5 178.0
Calculemos cada medida por separado
> min(Datos$Altura)
[1] 156
> max(Datos$Altura)
[1] 178
> quantile(Datos$Altura, probs = c(0.25, 0.75))
25% 75%
159.25 170.50
> mean(Datos$Altura)
[1] 166
> median(Datos$Altura)
[1] 167
f) Calcula el peso medio de los individuos y proporciona, al menos, dos medidas que indiquen la dispersión de esta variable
Para calcular el peso medio de los individuos, tenemos que tener en cuenta que la variable Peso incluye dos valores faltantes entre sus observaciones. Este hecho tiene que ser indicado estableciendo como TRUE el valor del parámetro na.rm
> mean(Datos$Peso, na.rm = TRUE)
[1] 67.25
El peso medio de los individuos es de 67,25 kg.
Como medidas de dispersión, se van a calcular la cuasi-varianza y el recorrido intercuartílico.
> var(Datos$Peso, na.rm = TRUE)
[1] 72.5
> IQR(Datos$Peso, na.rm = TRUE)
[1] 10.5
g) ¿Qué variable es más homogénea: la edad o la altura?
Para determinar la homogeneidad de una variable (o, lo que es lo mismo, la representatividad de su media), calculamos el coeficiente de variación para cada una de ellas, el cual se define como el cociente entre la desviación típica y la media de la variable.
Vamos a comenzar con la variable Edad. En primer lugar, calculemos la edad media de los individuos.
> media_Edad <- mean(Datos$Edad)
> media_Edad
[1] 34.6
A continuaciñon obtenemos la desviación típica. Para ello, calcularemos en primer lugar la varianza de la variable Edad mediante la función var, que recordemos calcula la cuasi-varianza de una variable.
> var_Edad <- 9/10 * var(Datos$Edad)
> var_Edad
[1] 148.04
Una vez obtenida la varianza, la desviación típica se obtiene como su raíz cuadrada positiva.
> dt_Edad <- sqrt(var_Edad)
> dt_Edad
[1] 12.16717
Por último, calculamos el coeficiente de variación de la Edad y mostramos su valor.
> CV_Edad <- dt_Edad/media_Edad
> CV_Edad
[1] 0.3516523
Repetimos el mismo proceso con la variable Altura.
> media_Altura <- mean(Datos$Altura)
> var_Altura <- 9/10 * var(Datos$Altura)
> dt_Altura <- sqrt(var_Altura)
> CV_Altura <- dt_Altura/media_Altura
> CV_Altura
[1] 0.04310492
La variable más homogénea es la variable Altura, ya que presenta un coeficiente de variación más próximo a 0.
Ejercicios Propuestos
Ejercicio Propuesto
Las siguientes tablas recogen información sobre el diámetro, la altura, el volumen del tronco y la variedad de distintos cerezos en dos regiones distintas: RegiónA y RegiónB
REGIÓN A
\( \begin{array} {|c|c|c|c|} \hline Diámetro & Altura & Volumen & Variedad \\ \hline 8.3 & 70 & 10.3 & Blanco \\ \hline 8.6 & 65 & 10.3 & Amarillo \\ \hline 8.8 & 63 & 10.2 & Rosa \\ \hline 10.5 & 72 & 16.4 & Rosa \\ \hline 10.5 & 81 & 18.8 & Rosa \\ \hline 10.8 & 83 & 19.7 & Rosa \\ \hline 11 & 66 & 15.6 & Blanco \\ \hline 11 & 75 & NA & Amarillo \\ \hline 11.1 & 80 & 22.6 & Rosa \\ \hline 11.2 & 75 & 19.9 & Blanco \\ \hline 11.3 & 79 & 24.2 & Amarillo \\ \hline 11.4 & 76 & 21 & Blanco \\ \hline 11.4 & 76 & 21.4 & Rosa \\ \hline 11.7 & 69 & 21.3 & Rosa \\ \hline 12 & 75 & 19.1 & Amarillo \\ \hline 12.9 & 74 & 22.2 & Amarillo \\ \hline 12.9 & 85 & 33.8 & Blanco \\ \hline \end{array} \)
REGIÓN B
\( \begin{array} {|c|c|c|c|} \hline Diámetro & Altura & Volumen & Variedad \\ \hline 13.3 & 86 & 27.4 & Amarillo \\ \hline 13.7 & 71 & 25.7 & Rosa \\ \hline 13.8 & 64 & 24.9 & Rosa \\ \hline 14 & 78 & NA & Amarillo \\ \hline 14.2 & 80 & 31.7 & Amarillo \\ \hline 14.5 & 74 & 36.3 & Rosa \\ \hline 16 & 72 & 38.3 & Rosa \\ \hline 16.3 & 77 & 42.6 & Rosa \\ \hline 17.3 & 81 & 55.4 & Blanco \\ \hline 17.5 & 82 & 55.7 & Blanco \\ \hline 17.9 & 80 & 58.3 & Amarillo \\ \hline 18 & 80 & NA & Rosa \\ \hline 18 & 80 & 51 & Blanco \\ \hline 20.6 & 87 & 77 & Rosa \\ \hline \end{array} \)
Tabla3. Datos del Ejercicio Propuesto
Se pide:
a) Crear dos conjuntos de datos, de nombre RegA y RegB que contengan la información recogida en las tablas anteriores
b) Representar la variable Variedad mediante un diagrama de sectores en cada región. Incluir un título descriptivo en cada gráfico y colorear los sectores de blanco, amarillo o rosa
c) Representar la variable Altura mediante un histograma en cada región
d) ¿Existe algún dato atípico en la variable Diámetro en la región A? ¿Y en la región B?
e) ¿Cuál es el valor máximo del 30% de los diámetros más pequeños de los cerezos de la región A? ¿Y el valor mínimo del 25% de las alturas mayores de los cerezos de la región B?
f) ¿Dónde es la variable volumen más homogénea: en la región A o en la región B?
g) ¿En qué región presentan los cerezos una altura media mayor? ¿En qué región presentan los cerezos una altura mediana menor?
h) Estudia la asimetría y la curtosis de la variable Diámetro en la región A.
Ejercicio Propuesto (Resuelto)
a) Crear dos conjuntos de datos, de nombre RegA y RegB que contengan la información recogida en las tablas anteriores
> diam<- c(8.3, 8.6, 8.8, 10.5, 10.5, 10.8, 11, 11, 11.1, 11.2, 11.3, 11.4, 11.4, 11.7, 12, 12.9, 12.9)
> alt<- c(70, 65, 63, 72, 81, 83, 66, 75, 80, 75, 79, 76, 76, 69, 75, 74, 85)
> vol<- c(10.3, 10.3, 10.2, 16.4, 18.8, 19.7, 15.6, NA, 22.6, 19.9, 24.2, 21, 21.4, 21.3, 19.1, 22.2, 33.8)
> var<- c(“B”, “A”, “R”, “R”, “R”, “R”, “B”, “A”, “R”, “B”, “A”, “B”, “R”, “R”, “A”, “A”, “B”)
> RegA<- data.frame (diam, alt, vol, var)
> RegA
diam alt vol var
1 8.3 70 10.3 B
2 8.6 65 10.3 A
3 8.8 63 10.2 R
4 10.5 72 16.4 R
5 10.5 81 18.8 R
6 10.8 83 19.7 R
7 11.0 66 15.6 B
8 11.0 75 NA A
9 11.1 80 22.6 R
10 11.2 75 19.9 B
11 11.3 79 24.2 A
12 11.4 76 21.0 B
13 11.4 76 21.4 R
14 11.7 69 21.3 R
15 12.0 75 19.1 A
16 12.9 74 22.2 A
17 12.9 85 33.8 B
b) Representar la variable Variedad mediante un diagrama de sectores en cada región. Incluir un título descriptivo en cada gráfico y colorear los sectores de blanco, amarillo o rosa
Diagrama de sectores de Variedad (Región A)
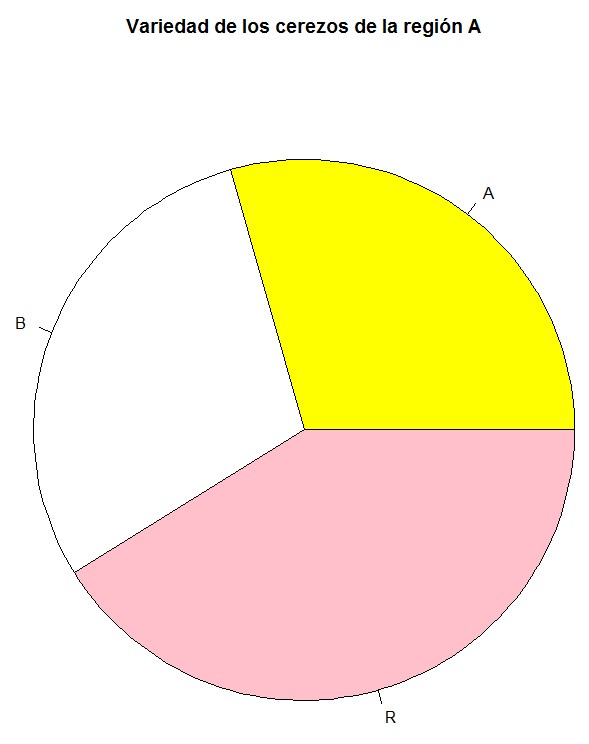 Figura 11: Diagrama de Sectores de Var (Región A)
Figura 11: Diagrama de Sectores de Var (Región A)
Diagrama de sectores de Variedad para la Región B
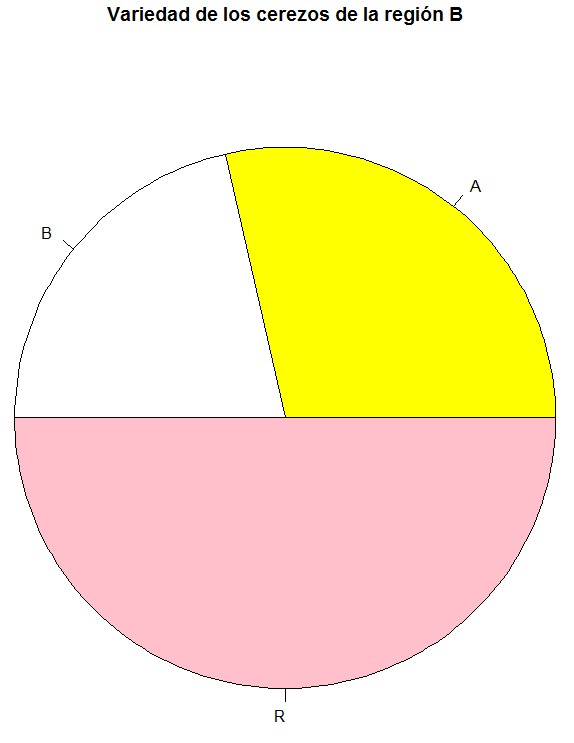 Figura 12: Diagrama de Sectores de Var (Región B)
Figura 12: Diagrama de Sectores de Var (Región B)
c) Representar la variable Altura mediante un histograma en cada región
Histograma de Altura en la Región A
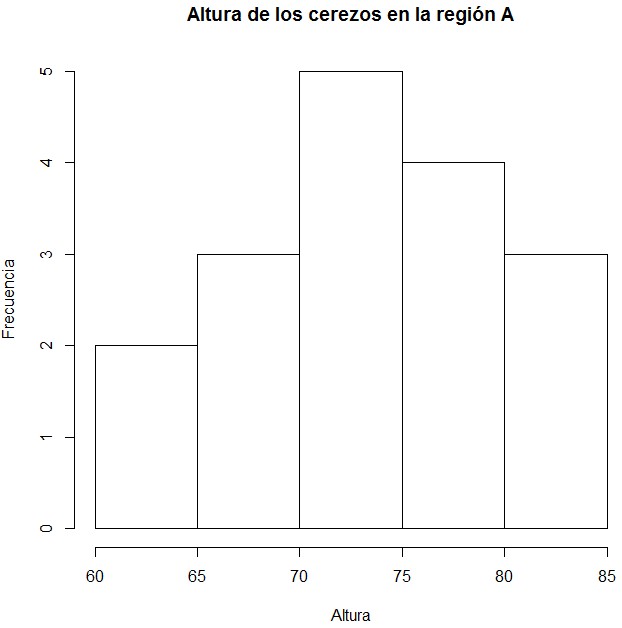 Figura 13: Histograma de la Altura (Región A)
Figura 13: Histograma de la Altura (Región A)
Histograma de la Altura para la Región B
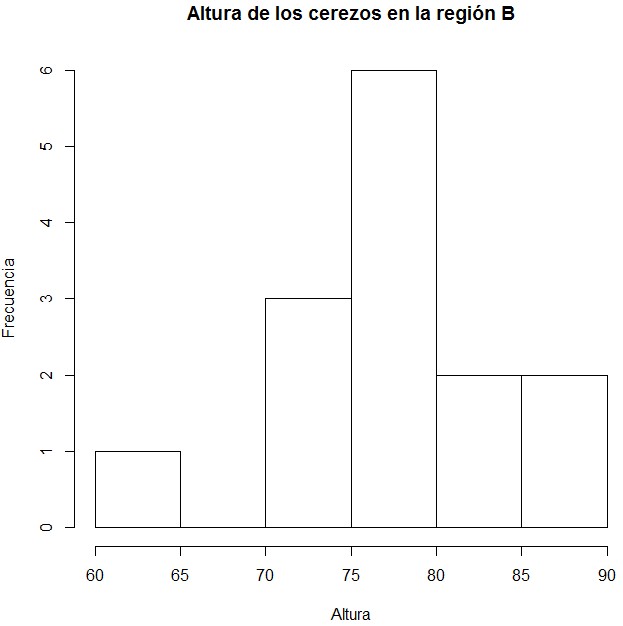 Figura 14: Histograma de la Altura (Región B)
Figura 14: Histograma de la Altura (Región B)
d) ¿Existe algún dato atípico en la variable Diámetro en la región A? ¿Y en la región B?
Para responder a esta pregunta, vamos a calcular los gráficos de caja y bigotes para la variable Diámetro en ambas regiones.
Boxplot de Diámetro para la Región A
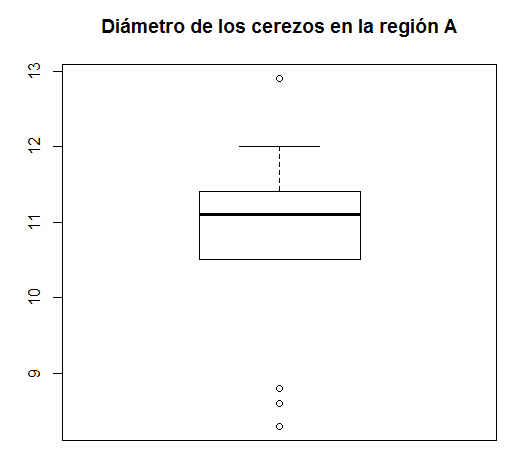 Figura 15: Caja y Bigotes de diámetro (Región A)
Figura 15: Caja y Bigotes de diámetro (Región A)
Boxplot de Diámetro de la Región B
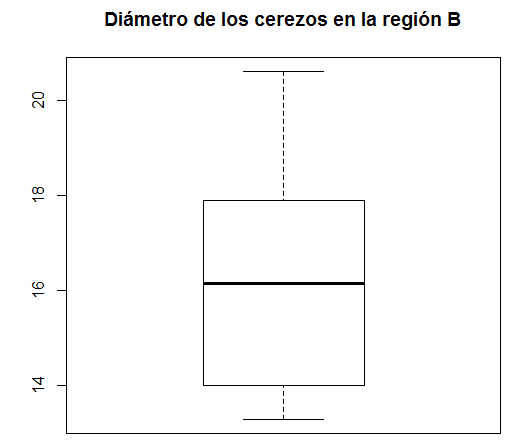 Figura 16: Caja y Bigotes de diámetro (Región B)
Figura 16: Caja y Bigotes de diámetro (Región B)
Hay cuatro valores atípicos (datos más allá de los extremos de los bigotes) para la variable Diámetro de la región A.
e) ¿Cuál es el valor máximo del 30% de los diámetros más pequeños de los cerezos de la región A? ¿Y el valor mínimo del 25% de las alturas mayores de los cerezos de la región B?
Los valores que nos están pidiendo son el percentil 30 de la variable Diámetro en la región A y el percentil 75 de la variable Altura en la región B, respectivamente.
Percentil 30 de Diámtero en la Región A = 10.74
Percentil 75 de la variable Altura en la región B = 80.75
f) ¿Dónde es la variable volumen más homogénea: en la región A o en la región B?
Para contestar a esta pregunta, vamos a calcular el coeficiente de variación para la variable Volumen en cada una de las regiones. Recordemos que la fórmula para el cómputo del coeficiente de variación (CV) es
\( CV= \displaystyle \frac{\sigma} {| \overline {x} | } \)
Fórmula 1: Coeficiente de Variación de Pearson
Por lo tanto,
CV de Volumen de la Región A = 0.3106773
CV de Volumne de la Región B = 0.3670137
Atendiendo a los resultados que hemos obtenido, podemos afirmar que la variable volumen es más homogénea en la región A, dado que es en esta región donde el coeficiente de variación para la variable volumen está más próximo a 0.
g) ¿En qué región presentan los cerezos una altura media mayor? ¿En qué región presentan los cerezos una altura mediana menor?
Como se puede apreciar, tanto la altura media como la altura mediana es mayor en la región B.
h) Estudia la asimetría y la curtosis de la variable Diámetro en la región A.
Asimetría de Diámetro en la Región A = -0.5608155
Kurtosis de Diámetro de la Región A = -0.4475198
Como el coeficiente de asimetría es menor que 0, concluiremos que la distribución de la variable Diámetro en la región A es asimétrica a la izquierda. Igualmente, dado que el coeficiente de curtosis es también negativo, la distribución de esta variable es menos apuntada que la distribución normal es decir, platicúrtica.
Autores: David Molina Muñoz y Ana María Lara Porras. Universidad de Granada. (2017)
Reformulado con MathML en 2021 por Ana María Lara Porras