DESCRIPCIÓN DE R: PRIMEROS PASOS
Objetivos
- Descargar e instalar el programa de análisis estadístico R
- Familiarizarse con el entorno de R
- Conocer los tipos de datos en R y realizar operaciones básicas con ellos
- Conocer las estructuras de datos en R y aprender a trabajar con ellas
- Importar conjuntos de datos desde ficheros de texto.
Descripción e instalación de R
R es un programa para el análisis estadístico de datos que se puede descargar de forma gratuita desde la dirección web http://www.r-project.org. Para ello, hay que pulsar la opción CRAN que aparece en el menú situado en la parte izquierda de la página.
Figura 1: Ubicación de la opción CRAN dentro de la página principal de R Project
A continuación, se elige en http://cran.r-project.org/mirrors.html el repositorio desde el cual se desea descargar el programa (conviene elegir un repositorio cercano para minimizar los tiempos de conexión). Elegimos Spain (https://cran.rediris.es/) en el menú situado a la izquierda de la página.
Figura 2: Elección del repositorio Spain (https://cran.rediris.es/)
Por último, se selecciona el sistema operativo en el que se va a instalar R (Windows, Linux o Mac). La figura siguiente muestra las tres opciones
- Download R for Linux
- Download R for(Mac) OS X
- Download R for Windows
Figura 3: Selección del sistema operativo
Para instalar R, en el sistema operativo Windows, elegir Dowload R for Windows. En la pantalla siguiente se elige, install R for the first. La instalación se encuentra en un ejecutable. Descargar el archivo de instalación y se muestra la siguiente pantalla
donde se muestran dos opciones: Guardar archivo y Cancelar. Elegimos Guardar archivo y una vez guardado lo ejecutamos. Se muestra la siguiente salida que es un asistente de instalación de R para Windows. Pulsamos la opción siguiente y el asistente realiza la instalación del programa
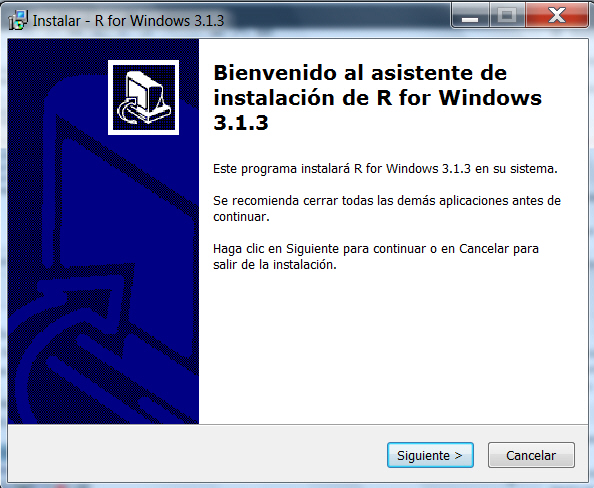Figura 5: Asistente de instalación para Windows
La instalación sólo realiza cambios mínimos en windows y copia los archivos necesarios en un directorio. Su desinstalación es sencilla y completa.
El directorio habitual donde realiza la instalación es C:/Archivos de programa. El programa crea en él un subdirectorio, R, y por cada versión un subdirectorio de este último donde copia todos los archivos, por ejemplo R-3.1.3. para la versión 3.1.3. En la instalación es conveniente seleccionar todas las opciones que se ofrecen, de tal modo que siempre se disponga de todas las ayudas posibles.
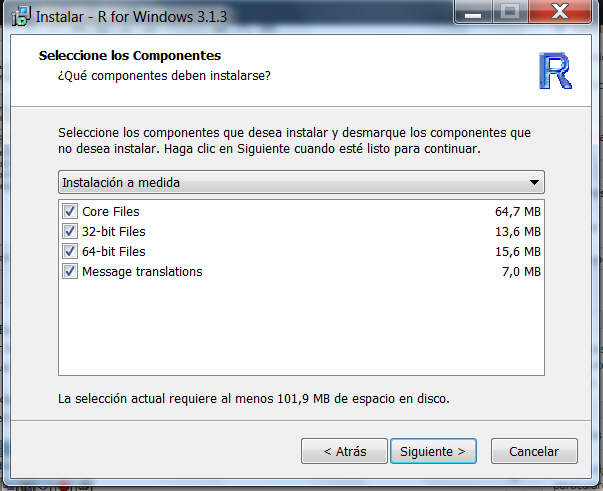Figura 6: Elección de las componentes de instalación
Resumen:
- En el sitio web: http://www.r-project.org: Ir a “CRAN” situado debajo de “Download” (en la parte izquierda de la pantalla, Figura 1),
- elegir país de descarga (España) (Figura 2: https://cran.rediris.es/)
- Seleccionar la versión correspondiente a nuestro sistema operativo (Linus, Windows o Mac) Figura 3
- Seguir las instrucciones de instalación del archivo ejecutable (Figura 5).
Una vez concluida la instalación, podemos ejecutar el programa desde cualquiera de los iconos que genera en el escritorio.
Figura 7: Interfaz de R
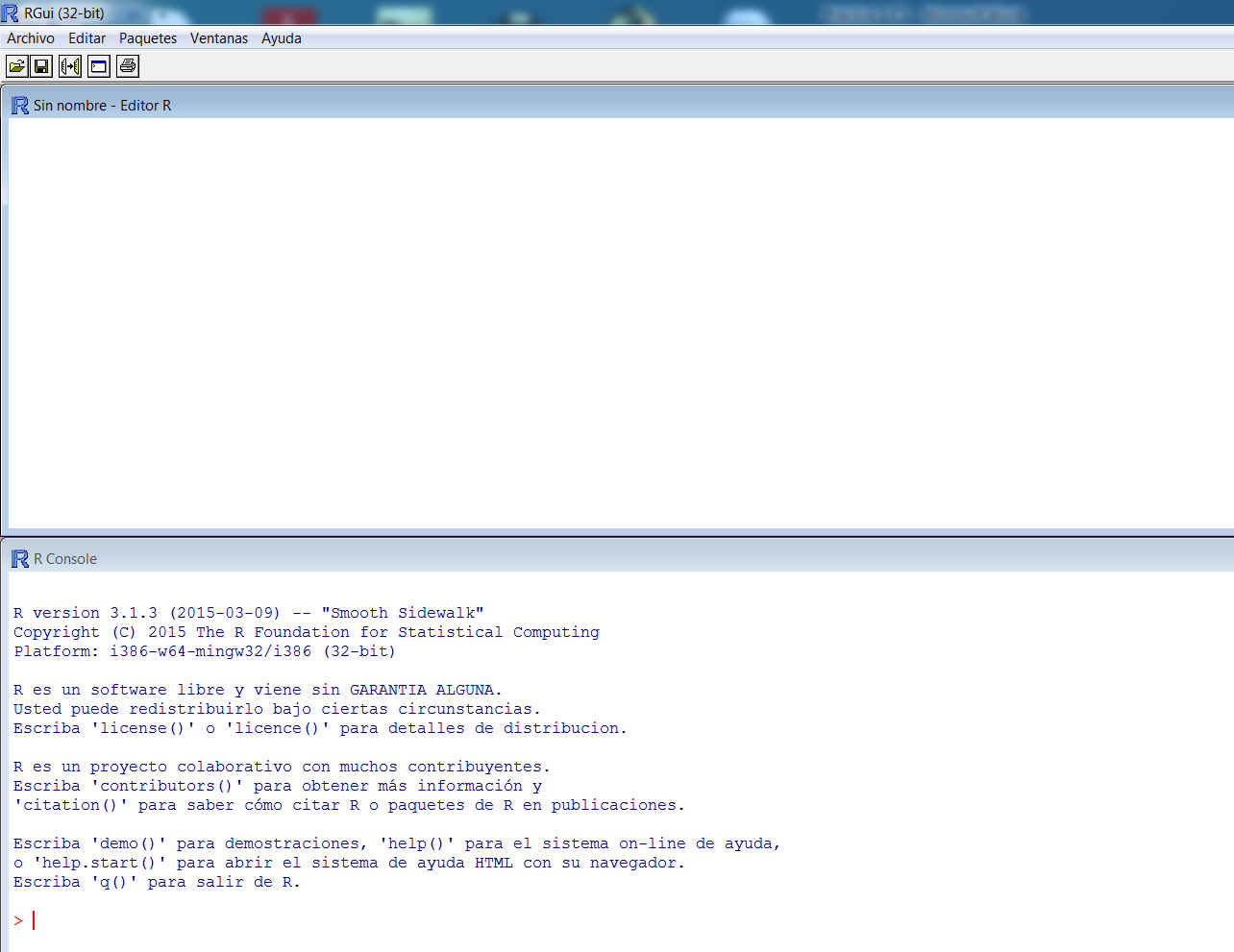
Al iniciar el programa R se muestra su interfaz de usuario (figura 7), que se compone de tres partes:
- Una barra de menús que permite acceder, por ejemplo, a funciones de ayuda y a opciones para la configuración de la apariencia del programa.
Es importante resaltar que, a diferencia de lo que ocurre con otros software estadístico, R no dispone de un menú que recoge todas las técnicas estadísticas que es capaz de llevar a cabo. Para realizar un análisis estadístico cualquiera en R, debemos introducir la expresión correspondiente en la consola, como veremos más adelante.
- Una barra de herramientas compuesta por un conjunto de botones que permite un acceso rápido a una serie de operaciones que se realizan con frecuencia.
Figura 9: Barra de herramientas
- Una consola en la que se muestra un breve mensaje inicial que contiene información sobre la versión actual del programa y algunas instrucciones básicas para su manejo.
Debajo del mensaje de apertura se encuentra el prompt, que es el símbolo “>”. Las expresiones en R se escriben a continuación del prompt.
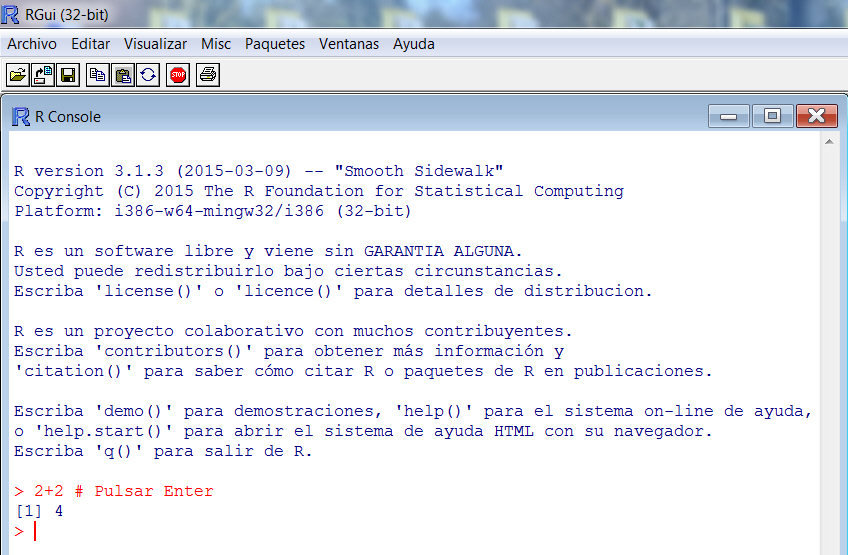
Por ejemplo, podemos escribir 2+2 en la consola a continuación del prompt, y tras pulsar la tecla “Enter”, nos devuelve en la misma consola el valor 4. (Recordar que estoy ejecutando R para Windows, el prompt de Linux y Mac es distinto).
> 2+2
[1] 4
Sin embargo, ésta no es la manera más eficiente de trabajar en R. Es muy útil manejar todas las entradas de código que solicitemos a R en un entorno donde podamos corregirlas, retocarlas, repetirlas, guardarlas para continuar el trabajo en otro momento, etc. Esta es la función del editor de R.
Barra del menú principal: Opciones
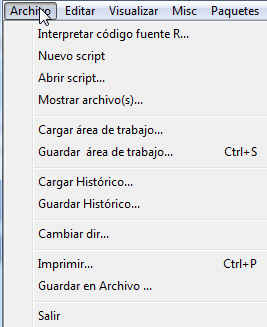
Figura 11: Opciones del menú Archivo.
Desde la barra del Menú principal se puede acceder a todos los menús de R. Los primeros menús: Archivo, Editar, Visualizar y Ayuda son habituales en los programas bajo Windows. El resto de menús son específicos de R. Cada uno de estos menús contiene distintas opciones que se muestran pulsando en cada una de ellos.
Mediante el Menú Archivo accedemos a un documento en blanco del editor, llamado script. Para ello, elegimos Archivo y a continuación Nuevo script (Archivo/Nuevo script)
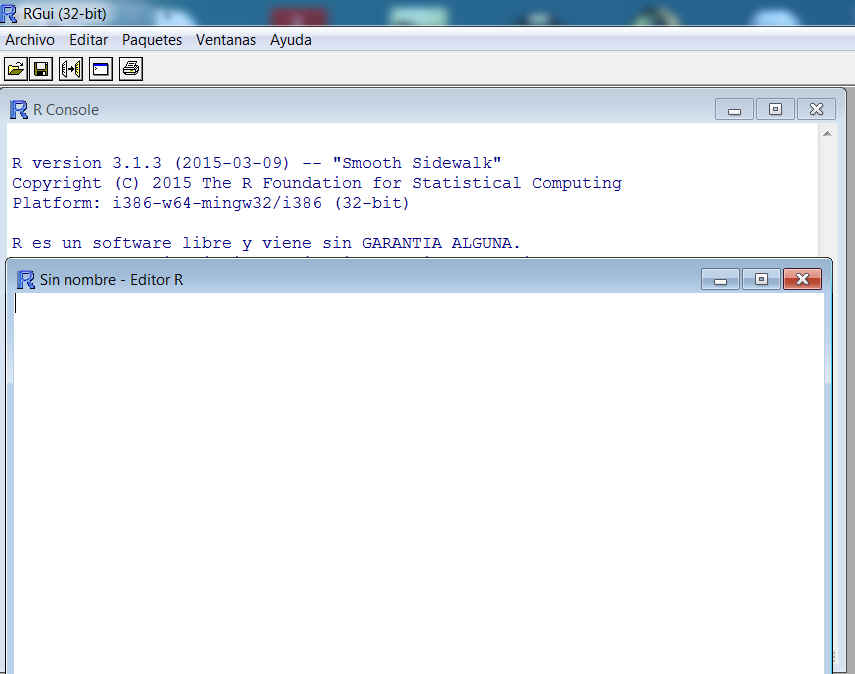Figura 12. La Consola y el Editor de R
Elegimos Divida horizontalmente en el menú Ventanas
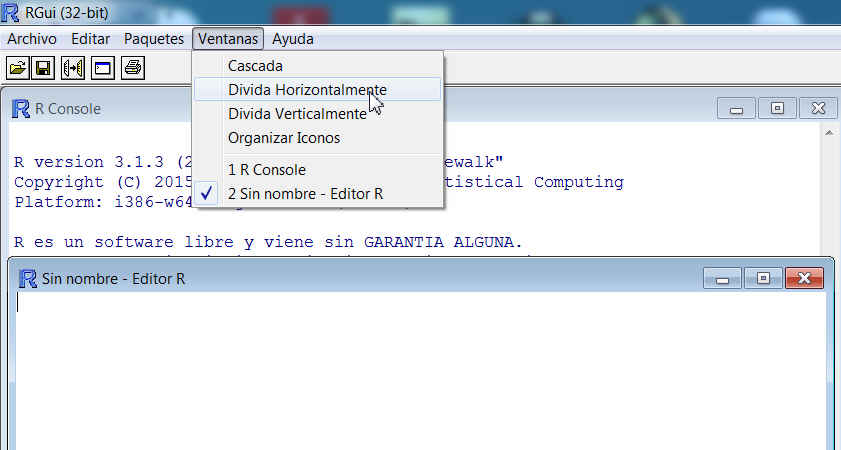Figura 13. La Consola y el Editor de R (Ventanas/Divida horizontalmente)
Y se muestran las pantallas de la Consola de R y Editor de R en paralelo, para que podamos escribir en una y otra con mayor facilidad.
Figura 14. La Consola y el Editor de R (Ambas pantallas en paralelo)
Un script o guion de trabajo nos permite escribir tantas líneas de código R como se deseen. A continuación se puede ejecutar todo o una parte del código escrito. El uso de scripts resulta especialmente útil cuando se ha de ejecutar un mismo código varias veces, puesto que nos ahorra el tener que teclear el código una y otra vez en la consola. Además, los scripts permiten la modificación del código de una forma cómoda y sencilla. Una vez creado, un script puede guardarse fácilmente.
Para ello, utilizaremos la opción Guardar o Guardar como …del menú Archivo de la consola. (Archivo/Guardar ó Ctrl+S; Archivo/Guardar como…)
Un script previamente guardado se puede recuperar mediante la opción Abrir script … del mismo menú. (Archivo/Abrir script…ó Ctrl+O)
En otras ocasiones, antes de finalizar una sesión de trabajo en R resulta conveniente guardar el área de trabajo. El área de trabajo contiene todos los objetos que se han definido en R durante la sesión de trabajo. Por objetos entendemos todas las variables, funciones y demás resultados que se hayan creado y que hayan sido nombrados de algún modo.
Para guardar el área de trabajo actual en cualquier momento de la sesión o cargar un área de trabajo guardada anteriormente se utilizan las opciones Archivo/Cargar área de trabajo… y Archivo/Guardar área de trabajo…, respectivamente.
R almacena un histórico con todas las órdenes que hemos ido ejecutando durante la sesión. Para navegar por las órdenes que conforman el histórico se utilizan las flechas arriba (↑) y abajo (↓) del teclado, las cuales muestran la orden anterior y la orden siguiente a una orden dada. Un histórico de instrucciones puede guardarse en cualquier momento mediante la opción Archivo/Guardar Histórico… Igualmente, se puede recuperar un histórico de instrucciones previamente guardado a través de la opción Archivo/Cargar Histórico…
Primeros pasos en R
Ejecutamos el programa desde el icono de R situado en el escritorio y se muestra una ventana, llamada consola (Figura 10), donde podemos manejar R mediante la introducción de código. En la consola R podemos escribir cada una de las instrucciones, o como hemos dicho anteriormente utilizamos el script para trabajar (Figura 13).
Funciones de ayuda
R es un software funcional, lo que quiere decir que realiza las tareas a través de funciones. La primera función que se va a presentar es “help“, la cual proporciona ayuda sobre cualquier función de R. Para acceder a la página de ayuda de una función, se escribe en la consola help seguido del nombre de la función a consultar entre paréntesis. Así, por ejemplo, si se desea obtener ayuda sobre la función mean (que, como se verá más adelante, calcula la media aritmética de un conjunto de datos), se debe teclear
> help (mean)
R muestra una pantalla de ayuda sobre la descripción de la media aritmética, su uso y ejemplos.
Una forma alternativa de obtener ayuda sobre una función es escribir el símbolo ? delante de su nombre.
> ?mean
Cuando no se conoce el nombre exacto de la función sino una o varias palabras claves, se puede utilizar la función “help.search“ para la búsqueda de ayuda. Si se escribe en la consola
> help.search(“median”)
R devuelve todas las funciones relacionadas con el cálculo de la mediana.
Tipos de datos
R permite trabajar con datos de distintos tipos. Los más comunes son:
- Numeric: Para datos de tipo numérico. A su vez, dentro del tipo numérico se pueden distinguir dos subtipos de datos:
-
- Integer: Para datos de tipo entero
- Double: Para datos de tipo real (o de doble precisión). Es el tipo de dato numérico que R considera por defecto, es decir, cuando se define un número en R, éste será de tipo double
- Logical: Para datos de tipo lógico o binario. Los valores que pueden tomar las variables de tipo lógico son TRUE o FALSE
- Character: Para caracteres o cadenas de caracteres.
Operaciones con tipos de datos
Creación de variables
Para crear una variable de tipo double (Datos de tipo real), basta con definir un valor numérico cualquiera.
> doub <- 4 # Escribimos doub <- 4 en la consola y pulsamos la tecla “Enter”
Nota: Es posible incluir comentarios que R no leerá si utilizamos líneas que comiencen con el carácter #.
En el ejemplo anterior, mediante el operador <- se asigna a la variable doub el valor 4 (<- es un operador de asignación en R). En las nuevas versiones de R se puede utilizar el signo = en lugar de <-.
> doub=4 # Asigna el valor 4 a la variable doub
> doub # muestra el valor de la variable doub
[1] 4
Para definir variables de tipo integer, se aplica la función as.integer() a un dato de tipo numérico.
> int = as.integer(4)
> int # muestra el valor de la variable int
[1] 4
Una variable lógica se define asignando el valor TRUE o FALSE a una variable.
> logi = FALSE
> logi
[1] FALSE
Por último, R considera como cadena de caracteres cualquier cosa encerrada entre comillas dobles (“”).
> char1 = “Hola” # cuidado con las comillas son las de la tecla del número 2
> char1
[1] “Hola”
> char2 <- “5 + 6”
> char2
[1] “5 + 6”
Comprobación del tipo de una variable
Para determinar el tipo de una variable se aplica la función typeof() sobre la variable en cuestión.
> typeof(doub)
[1] “double”
> typeof(int)
[1] “integer”
> typeof(char1)
[1] “character”
Operadores básicos
R puede utilizarse como una calculadora, ya que tiene implementadas las principales operaciones aritméticas como son la suma, la diferencia, el producto, la división, la exponenciación, la división entera y el módulo de la división. Estas operaciones se realizan mediante los símbolos +, -, *, /, ^, %/% y %%, respectivamente.
> 2^3
[1] 8
> 9/6
[1] 1.5
> 9%/%6
[1] 1
> 9%%6
[1] 3
Como se ha visto anteriormente, en R es posible definir variables asignándoles un determinado valor o, incluso, el resultado de una operación. Existen 3 operadores de asignación diferentes: <- , = y ->. Los dos primeros evalúan la expresión situada en la parte derecha y asignan el resultado a la variable de la parte izquierda, mientras que el último realiza la asignación de forma inversa, de manera que es el resultado de la evaluación de expresión de la parte izquierda el que se asigna a la variable de la derecha.
> a = 2 + 2 # resultado de 2+2 se asigna a la variable a
> b = 3 * 2 # resultado de 3*2 se asigna a la variable b
> b – a -> c # resultado de b-a se asigna a la variable c
> a
[1] 4
> b
[1] 6
> c
[1] 2
En el ejemplo anterior, las variables a y b recogen el resultado de una suma y un producto, respectivamente. Es decir, primero se realiza la operación y el resultado es el que se almacena en la variable.
Por otra parte, existen varios operadores que permiten establecer comparaciones entre variables. Son los denominados operadores comparativos, que en R vienen representados por los símbolos == (igual a), != (distinto a), < (menor que), > (mayor que), <= (menor o igual que) y >= (mayor o igual que). Estos operadores se caracterizan por ser binarios, esto es, únicamente permiten comparaciones entre dos elementos. Para comparaciones más complejas, se utilizan los operadores lógicos. Los más utilizados son & (AND ó “y lógico”) y | (OR u “o lógico”).
> a == 5
[1] FALSE
> a == 4 & b < 2
[1] FALSE
> a == 4 | b < 2
[1] TRUE
> a == 4 | b < 2 & c != 9
[1] TRUE
Otras funciones interesantes
Además de las operaciones elementales, R tiene implementadas una amplia variedad de funciones que permiten la realización de cálculos más complejos. A continuación se muestran algunas de ellas:
sqrt(x) : Raíz cuadrada de x
abs(x) : Valor absoluto de x
sin(x) : Seno de x
cos(x) : Coseno de x
tan(x) : Tangente de x
log(x) : Logaritmo neperiano de x
log10(x) : Logaritmo decimal de x
exp(x) : Exponencial de x
Estructuras de datos
Hasta el momento se ha visto que se pueden definir variables en R que almacenen valores o resultados de operaciones. Pero cuando se desea guardar un número elevado de valores conviene organizarlos en estructuras de datos. Las estructuras de datos más utilizadas en R son
- Arrays. Pueden tener varias dimensiones pero admiten únicamente un tipo de dato. Dependiendo del número de dimensiones, se distingue entre
- Vectores. Una dimensión
- Matrices. Dos dimensiones
- Arrays. Tres o más dimensiones.
- Factores. Se utilizan para almacenar variables cualitativas en las que no existe un orden específico entre las categorías.
- Factores ordenados. Almacenan variables cualitativas ordinales, es decir, variables cualitativas con un cierto orden entre sus categorías.
- Data frames. Admite variables de distintos tipos, pero con la misma longitud.
- Listas. La lista es la estructura de datos más flexible puesto que permite incluir variables de tipos y longitudes diferentes.
Creación de estructuras de datos
Una vez presentadas las estructuras de datos, el siguiente paso es aprender a crearlas.
Vectores: Para crear un vector se utiliza la función c, que concatena todos los elementos que recibe como argumentos.
c(elemento1, elemento2, elemento3, …)
Matrices: Las matrices se definen mediante la función matrix. Para ello, se ha de indicar qué datos va a tener la matriz, así como el número de filas y columnas.
matrix(data = NA, nrow = 1, ncol = 1, byrow = FALSE,…)
Por defecto, la función matrix considera una matriz con una sola fila y una sola columna con valor NA (Not Available). El argumento byrow indica si la matriz se irá completando por columnas (byrow = FALSE, que es la opción por defecto) o por filas (byrow = TRUE). Modificando estos argumentos se pueden definir distintas matrices según las necesidades que se tengan.
Arrays: Los arrays se crean a través de la función array, especificando el conjunto de datos que va a formar parte del array así como las dimensiones del mismo.
array(data = NA, dim,…)
Factores y factores ordenados: Los factores y factores ordenados en R se crean utilizando las funciones factor y ordered, respectivamente. Estas funciones necesitan como argumentos el conjunto de datos y los niveles o categorías del factor.
factor(x, levels,…)
ordered(x, levels,…)
Un detalle muy importante que hay que tener en cuenta a la hora de definir los niveles de un factor ordenado es que R considera que los niveles vienen dados de menor a mayor, es decir, que si dentro de la función ordered se especifica que levels = c(2, 1, 3), R entiende que la primera categoría es menor que la segunda y que la segunda es, a su vez, menor que la tercera, esto es, que 2 < 1 < 3.
Data frame y lista: Los data frame y las listas en R se crean utilizando las funciones data.frame y list, respectivamente, indicando las variables que conformarán la estructura de datos.
data.frame(variable1, variable2, variable3,…)
list(variable1, variable2, variable3,…)
Veamos algunos ejemplos:
Vectores
> vec = c(1, 3, 14)
> vec
[1] 1 3 14
Matrices
> mat1 <- matrix(c(1,2,3,4,5,6), nrow = 2, ncol = 3) # por defecto las matrices se completan por columna
> mat1
[,1] [,2] [,3]
[1,] 1 3 5
[2,] 2 4 6
> mat2 <- matrix(c(1,2,3,4,5,6), nrow = 2, ncol = 3, byrow = TRUE) # byrow = TRUE indica que complete la matriz por filas
> mat2
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
Nota: Las matrices mat1 y mat2 tienen los mismos elementos, pero en la primera de ellas están dispuestos por columnas, mientras que en la segunda se han colocado por filas.
Array
> arr <- array(c(1,2,3,4,5,6,7,8), dim = c(2,2,2))
> arr
, , 1
[,1] [,2]
[1,] 1 3
[2,] 2 4
, , 2
[,1] [,2]
[1,] 5 7
[2,] 6 8
Matrices
> m <- matrix(c(1,1,2,1),2,2)
> m
[,1] [,2]
[1,] 1 2
[2,] 1 1
Factores y Factores ordenados
> fac <- factor(c(“H”,”M”,”M”,”H”,”H”,”M”), levels = c(“H”,”M”))
> ord <- ordered(c(1,2,1,2,3,1,2,1,2), levels = c(1,2,3))
Como se ha resaltado antes, es muy importante tener en cuenta el orden en el que se indican los niveles de la variable en un factor ordenado. En un factor (no ordenado), el orden en el que aparecen las categorías de la variable es irrelevante. Así, mientras que los factores ordenados
> ord <- ordered(c(1,2,1,2,3,1,2,1,2), levels = c(1,2,3))
> ord2 <- ordered(c(1,2,1,2,3,1,2,1,2), levels = c(2,3,1))
> ord3 <- ordered(c(1,2,1,2,3,1,2,1,2), levels = c(3,1,2))
son distintos, estos otros factores no ordenados
> fac <- factor(c(“H”,”M”,”M”,”H”,”H”,”M”), levels = c(“H”,”M”))
> fac2 <- factor(c(“H”,”M”,”M”,”H”,”H”,”M”), levels = c(“M”,”H”))
son totalmente equivalentes.
Data frames y Listas
> a <- c(1,5,4)
> b <- c(“hola”, “adiós”, “hasta luego”)
> c <- c(TRUE, FALSE, FALSE)
> d <- c(1,2,3,4,5)
> dataframe <- data.frame(a, b, c)
> dataframe
a b c
1 1 hola TRUE
2 5 adiós FALSE
3 4 hasta luego FALSE
> list1 <- list(a, b, c)
> list1
[[1]]
[1] 1 5 4
[[2]]
[1] “hola” “adiós” “hasta luego”
[[3]]
[1] TRUE FALSE FALSE
> list2 <- list(a, b, c, d)
> list2
[[1]]
[1] 1 5 4
[[2]]
[1] “hola” “adiós” “hasta luego”
[[3]]
[1] TRUE FALSE FALSE
[[4]]
[1] 1 2 3 4 5
Acceso a los elementos de las estructuras de datos
Una vez definida una estructura de datos, es importante conocer cómo acceder a los elementos que la componen.
En un array (sea cual sea su dimensión), se utilizan los corchetes ([]), dentro de los cuales se indica la posición del elemento al que queremos acceder en cada una de las dimensiones del array.
> vec <- c(1, 3, 14)
> vec[3]
[1] 14
> mat1 <- matrix(c(1,2,3,4,5,6), nrow = 2, ncol = 3)
> mat1
[,1] [,2] [,3]
[1,] 1 3 5
[2,] 2 4 6
> mat1[2, 3]
[1] 6
> arr <- array(c(1,2,3,4,5,6,7,8), dim = c(2,2,2)) # el ultimo 2 indica que son dos matrices
> arr
, , 1
[,1] [,2]
[1,] 1 3
[2,] 2 4
, , 2
[,1] [,2]
[1,] 5 7
[2,] 6 8
> arr[2, 1, 2] # el elemento de la segunda fila primera columna de la segunda matriz
[1] 6
También se puede acceder a varios elementos al mismo tiempo usando la función de concatenación c.
> mat1[c(1,2), 3] # los elementos (1, 3) y (2, 3) de la matriz
[1] 5 6
En el ejemplo anterior se obtienen dos elementos de la matriz mat1. El primero situado en la primera fila y tercera columna y el segundo situado en la segunda fila y tercera columna.
Para acceder a una fila completa, se indica el número de fila y no se indica ninguna columna.
> mat1[1,]
[1] 1 3 5
Del mismo modo se puede acceder a columnas completas
> mat1[, c(1,2)]
[,1] [,2]
[1,] 1 3
[2,] 2 4
Al igual que en el caso de los arrays, para acceder a un elemento de un factor o de un factor ordenado también se emplean los corchetes ([]), indicando la posición de dicho elemento.
> fac[2]
[1] M
Levels: H M
> ord[c(2, 5)]
[1] 2 3
Levels: 1 < 2 < 3
En los data frames se utiliza el símbolo $ seguido del nombre de la columna dentro del data frame.
> dataframe$a
[1] 1 5 4
Recordemos que un data frame está formado por distintas columnas de igual longitud. Cada una de estas columnas es en realidad un vector de manera que, una vez se ha especificado la columna del data frame a la que se desea acceder (mediante el símbolo $), es posible obtener valores de la columna usando los corchetes. Así, por ejemplo, para obtener el primer valor dentro de la columna de nombre a incluida en el data frame que se llama dataframe se tiene que escribir
> dataframe$a[1]
[1] 1
Alternativamente, un data frame puede verse como una matriz por tanto, también pueden usarse los corchetes ([]) para acceder a sus elementos.
> dataframe[1,]
a b c
1 1 hola TRUE
Para acceder a un elemento dentro de una lista, se emplean los corchetes dobles ([[]]) y se indica dentro de ellos qué posición ocupa el elemento a acceder.
> list1[[2]]
[1] “hola” “adiós” “hasta luego”
> list2[[4]][2]
[1] 2
Ejemplos
> peso <- c(19,14,15,17,20,23,30,19,25)
> peso < 20
> peso < 20 | peso > 25
> peso[peso < 20]
> peso[peso < 20 & peso != 15]
> trat <- c(rep(“A”, 3), rep(“B”, 3), rep(“C”, 3))
> peso[trat == “A”]
> peso[trat == “A” | trat == “B”]
> split(peso, trat)
> split(peso, trat)$A
> x <- 1:15; length(x) # varias instrucciones en un mismo renglón separadas por ;
> y <- matrix(5, nrow = 3, ncol = 4); dim(y)
> is.vector(x); is.vector(y); is.array(x)
> x1 <- 1:5; x2 <- c(1, 2, 3, 4, 5); x3 <- “patata”
> typeof(x1); typeof(x2); typeof(x3)
> mode(x); mode(y); z <- c(TRUE, FALSE); mode(z)
> attributes(y)
> w <- list(a = 1:3, b = 5); attributes(w)
> y <- as.data.frame(y); attributes(y)
Ejemplos: Generación de secuencias
> x <- c(1, 2, 3, 4, 5)
> x <- 1 : 10 ; y <- -5 : 3
> 1 : 4 + 1; 1 : (4 + 1)
> x <- seq(from = 2, to = 18, by = 2) # la function seq genera una secuencia
> x <- seq(from = 2, to = 18, length = 30)
> y <- seq(along = x)
> z <- c(1 : 5, 7:10, seq(from=-7, to=5, by=2))
> rep(1, 5) #repite el 1 cinco veces
> x <- 1:3; rep(x, 2)
> y <- rep(5, 3); rep(x, y)
> rep(1 : 3, rep(5, 3))
> rep(x, x)
> rep(x, length = 8)
> gl(3, 5) # es equivalente a rep(1:3, rep(5, 3))
> gl(4, 1, length = 20) # gl genera factores
> gl(3, 4, label = c(“Rubio”, “Moreno”, “Pelirrojo”))
Nota: Para generar secuencias también podemos usar las funciones seq y rep
Ejemplos: Selección de los elementos de un vector
> x <- 1:7; x[1]; x[3]; x[c(2,6)] # el ; separa instrucciones
> x[x > 4]
> x > 4
> y <- x > 4
> x[y]
> x[-c(1, 5)]; y <- c(1, 2, 6); x[y]
> names(x) <- c(“a”, “b”, “c”, “d”, ”e”, “manzana”) # Cuidado con las dobles las comillas (tecla del 2)
> x[c(“a”, “e”, “manzana”)]
Ejemplos. Ordenación de vectores
> x <- c(7, 4, 5, 9, 1)
> order(x)
> sort(x)
> rev(x)
> rank(x)
> x[order(x)]
> y <- c(1, 5, 5, 5, 7, 7, 9, 9, 9, 9); rank(x, y)
> min(x); which.min(x); which(x == min(x))
> y <- c(1, 1, 2, 2, 3); order(y, x)
Ejemplos de vectores de caracteres
> paste1 <- paste(c(“I”, “J”, “M”), 3:5, sep = “”)
> paste2 <- paste(c(“I”, “J”, “M”), 3:5, sep = “.”)
> unir1 <- paste(c(“el”, “sol”, “brilla”), collapse =” “)
> unir2 <- paste(c(“el”, “sol”, “brilla”), collapse =”-“)
> unir3 <- paste(c(“el”, “sol”, “brilla”))
> letras <- LETTERS[1:9]; números <- 7:15
> unir4 <- paste(letras, números, sep =””)
> substr(“abcdef”, 2, 4)
> x <- paste(LETTERS[1:7], collapse = “”)
> substr(x, 3, 7) <- c(“xyz”)
> x <- c(60, 90, 903); y <- factor(x); x ; y
> as.numeric(as.character(y)) # convierte un vector factor en numérico
> factor1 <- factor(c(“alto”, “bajo”, “medio”))
> factor2 <- factor(c(“alto”, “bajo”, “medio”), levels = c(“bajo”, “medio”, “alto”)) # cambia el orden de las etiquetas
Ejemplos de arrays y matrices
> a <- 1:24; dim(a) <- c(3,4,2)
> arr1 <- array(7, dim = c(4,5))
> mat1 <- matrix(10:29, nrow = 5)
> mat2 <- matrix(10:29, nrow = 5, byrow = TRUE)
> mat3 <- 10:29; dim(mat3) <- c(5, 4)
> a[1,1,1]; a[1,1,2]; a[3,4,2]
> a[2, , ] # es un array de dimensión c(4,2)
> a[,3 , ] # es un array de dimensión c(3,2)
> mat3[1, ]; mat3[, 2]; mat3[c(1, 3), c(2, 4)]
> mat4 <- matrix(c(1, 3, 2, 4), nrow = 2); mat4
> mat3[mat4] # coordenadas matricialmente
> m1 <- matrix(1: 4, nr = 2, nc = 2)
> m2 <- matrix(6: 9, nr = 2, nc = 2)
> rbind(m1, m2) # rbind une matrices por filas
> cbind(m1, m2) # cbind une matrices por columnas
> diag(m1) # diagonal principal de la matriz
Ejemplos de Data frames y listas
> x <- 1:4; n <- 10; M <- c(10, 35); y <- 2:5 ; x; n; M; y
> data.frame(x, n)
> data.frame(x, M)
> data.frame(x, y)
> l1 <- list(x, y); l2 <- list(A = x, B = y) ; l1; l2
> names(l1)
> names(l2)
Lectura de datos desde ficheros externos
Cuando se trabaja con R es posible introducir los datos tecleándolos directamente e ir visualizándolos en la consola a medida que los escribimos. Sin embargo, no es la opción más habitual, ya que la introducción manual de datos es una tarea tediosa, especialmente cuando se tiene un gran volumen de información. En estos casos, lo más normal es disponer de un fichero de datos que el programa se encarga de leer. R es capaz de leer ficheros con multitud de formatos: Excel (con extensión .xls o .xlsx), SPSS (con extensión .sav),… Uno de los formatos más utilizado para almacenar datos es el formato fichero de texto (con extensión .txt). Los ficheros con extensión .txt son muy ligeros y sencillos de utilizar. Para leer un fichero .txt en R se emplea la función read.table
read.table(file, header = FALSE,…)
El primer argumento de la función, file, hace referencia a la ruta en la cual está el fichero a leer. Este argumento, al ser una cadena de caracteres, ha de ir entre comillas dobles. Un detalle importante a tener en cuenta es que en R la barra que se emplea para especificar una ruta es la barra / en lugar de la barra \ habitual.
Por otra parte, el segundo argumento es un argumento lógico mediante el cual se indica si en el fichero de texto que vamos a leer aparecen los nombres de las variables en la primera línea (en ese caso, header = TRUE) o no apacecen (entonces, header = FALSE, que es la opción por defecto).
Al emplear esta función, read.table, se obtiene un data frame con todas las observaciones de todas las variables incluidas en el fichero de texto.
Ejercicios
Ejercicios Guiados
Ejercicio guiado1
En la siguiente tabla se recogen datos acerca de la raza, la edad, el peso y la altura de 10 personas:
\( \begin{array} {|c|c|c|c|} \hline Raza & Edad & Peso & Altura \\ \hline Blanca & 24 & 58 & 156 \\ \hline Negra & 26 & 62 & 175 \\ \hline Blanca & 62 & 61 & 169 \\ \hline Blanca & 31 & 67 & 171 \\ \hline Negra & 30 & 71 & 159 \\ \hline Negra & 41 & 69 & 160 \\ \hline Negra & 51 & 68 & 158 \\ \hline Blanca & 23 & 73 & 178 \\ \hline Blanca & 28 & 56 & 168 \\ \hline Blanca & 30 & 82 & 156 \\ \hline \end{array} \)
Tabla 1. Datos del Ejercicio Guiado 1
a) Elaborar un fichero de texto (con extensión .txt) que contenga la información de la tabla anterior. Utilizar el tabulador para separar la información referente a cada variable. Guárdalo en el escritorio y llámarlo mibasededatos.txt.
b) Desde R leer el fichero que se acaba de crear y almacenar su contenido en una variable de nombre datos.
c) Obtener los valores para las 4 variables para el tercer y el séptimo individuo
d) Determinar la altura del noveno individuo
e) Comprobar si la edad del primer individuo es mayor que la edad del último individuo
f) Comprobar si el peso conjunto de los dos primeros individuos es menor que el peso conjunto de los dos últimos
g) Calcular la raíz cuadrada de la altura del quinto individuo.
Ejercicio guiado2
La siguiente tabla incluye información acerca del sexo de seis estudiantes, sus puntuaciones en la asignatura de Estadística y la opinión que tienen acerca de la asignatura (Buena, Regular o Mala)
\( \begin{array} {|c|c|c|} \hline Sexo & Puntuación & Opinión \\ \hline Hombre & 7.5 & Buena \\ \hline Mujer & 8 & Regular \\ \hline Mujer & 2 & Mala \\ \hline Mujer & 6.5 & Mala \\ \hline Mujer & 10 & Regular \\ \hline Hombre & 9 & Buena \\ \hline \end{array} \)
Tabla 2. Datos del Ejercicio Guiado 2
Se pide:
a) Almacenar el contenido de la tabla en tres variables distintas (Sexo, Puntuación y Opinión), seleccionando el tipo de variable adecuado en cada caso
b) Crear un data frame de nombre Estudiantes que contenga la información de las tres variables creadas
c) La puntuación media de los hombres y de las mujeres
d) Los datos de las tres variables para el quinto individuo
e) El logaritmo neperiano de la puntuación del tercer individuo
f) Comprobar si la puntuación del segundo individuo o del cuarto individuo es superior a 7.
Ejercicio Guiado 1 (Resuelto)
En la siguiente tabla se recogen datos acerca de la raza, la edad, el peso y la altura de 10 personas:
\( \begin{array} {|c|c|c|c|} \hline Raza & Edad & Peso & Altura \\ \hline Blanca & 24 & 58 & 156 \\ \hline Negra & 26 & 62 & 175 \\ \hline Blanca & 62 & 61 & 169 \\ \hline Blanca & 31 & 67 & 171 \\ \hline Negra & 30 & 71 & 159 \\ \hline Negra & 41 & 69 & 160 \\ \hline Negra & 51 & 68 & 158 \\ \hline Blanca & 23 & 73 & 178 \\ \hline Blanca & 28 & 56 & 168 \\ \hline Blanca & 30 & 82 & 156 \\ \hline \end{array} \)
Tabla 1. Datos del Ejercicio Guiado 1
Se pide:
a) Elaborar un fichero de texto (con extensión .txt) que contenga la información de la tabla anterior. Utilizar el tabulador para separar la información referente a cada variable. Guárdalo en el escritorio y llámarlo mibasededatos.txt.
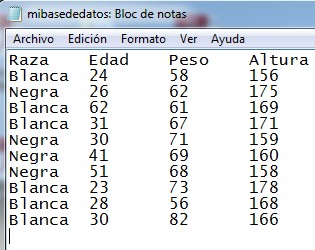
Creamos un fichero de texto que recoja la información que muestra la tabla y lo guardamos en el escritorio con el nombre mibasededatos.txt. El fichero tendrá un aspecto parecido a éste
b) Desde R leer el fichero que se acaba de crear y almacenar su contenido en una variable de nombre datos.
Teniendo en cuenta que el fichero de datos contiene el nombre de las variables en la primera línea, la orden que tenemos que emplear es
> datos <- read.table(“C:/Users/Usuario/Desktop/mibasededatos.txt”, header = TRUE) # Cuidado con las dobles las comillas (tecla “)
Nota: La ruta hasta llegar al fichero varía en función del ordenador. Utilizar la siguiente orden para situarse en el directorio de trabajo
> setwd(“C:/Users/Usuario/Desktop/nombrecarpeta”)
> datos <- read.table(“mibasededatos.txt”, header = TRUE)
Después de leer el fichero de datos, veamos qué aspecto tiene la variable datos
> datos
Raza Edad Peso Altura
1 Blanca 24 58 156
2 Negra 26 62 175
3 Blanca 62 61 169
4 Blanca 31 67 171
5 Negra 30 71 159
6 Negra 41 69 160
7 Negra 51 68 158
8 Blanca 23 73 178
9 Blanca 28 56 168
10 Blanca 30 82 166
c) Obtener los valores para las 4 variables para el tercer y el séptimo individuo
Vamos a leer de forma conjunta las filas 3 y 7 del data frame.
> datos[c(3,7),]
Raza Edad Peso Altura
3 Blanca 62 61 169
7 Negra 51 68 158
d) Determinar la altura del noveno individuo
Tenemos dos formas de conocer la altura del individuo
> datos$Altura[9]
[1] 168
o bien
> datos[9,4]
[1] 168
e) Comprobar si la edad del primer individuo es mayor que la edad del último individuo
En este caso, tenemos que realizar una comparación simple
> datos$Edad[1] > datos$Edad[10]
[1] FALSE
f) Comprobar si el peso conjunto de los dos primeros individuos es menor que el peso conjunto de los dos últimos
> datos$Peso[1] + datos$Peso[2] < datos$Peso[9] + datos$Peso[10]
[1] TRUE
g) Calcular la raíz cuadrada depropuesto 2
la altura del quinto individuo
> sqrt(datos$Altura[5])
[1] 12.60952
Ejercicio Guiado 2 (Resuelto)
La siguiente tabla incluye información acerca del sexo de seis estudiantes, sus puntuaciones en la asignatura de Estadística y la opinión que tienen acerca de la asignatura (Buena, Regular o Mala)
\( \begin{array} {|c|c|c|} \hline Sexo & Puntuación & Opinión \\ \hline Hombre & 7.5 & Buena \\ \hline Mujer & 8 & Regular \\ \hline Mujer & 2 & Mala \\ \hline Mujer & 6.5 & Mala \\ \hline Mujer & 10 & Regular \\ \hline Hombre & 9 & Buena \\ \hline \end{array} \)
Tabla 2. Datos del Ejercicio Guiado 2
Se pide:
a) Almacenar el contenido de la tabla en tres variables distintas (Sexo, Puntuación y Opinión), seleccionando el tipo de variable adecuado en cada caso.
La variable Sexo es una variable cualitativa sin un orden específico entre sus categorías, de modo que crearemos un factor no ordenado para almacenar la información de esta variable.
La variable Opinión es una variable cualitativa con un orden entre sus categorías (Mala < Regular < Buena), por lo que crearemos un factor ordenado para almacenar la información de dicha variable
La variable Puntuación almacena en un vector de números reales.
> sexo <- factor (c(“H”, “M”, “M”, “M”, “M”, “H”), levels = c(“H”, “M”))
> opinion <- ordered (c(“B”, “R”, “M”, “M”, “R”, “B”), levels = c(“M”, “R”, “B”))
> puntuacion <- c(7.5, 8, 2, 6.5, 10, 9)
>sexo
[1] H M MMM H
Levels: H M
>opinion
[1] B R M M R B
Levels: M < R < B
>puntuacion
[1] 7.5 8.0 2.0 6.5 10.0 9.0
Nota: No olvidar que en R el signo decimal viene dado por el punto (.) y no por la coma (,)
b) Crear un data frame de nombre Estudiantes que contenga la información de las tres variables creadas
>estudiantes<- data.frame(sexo, puntuacion, opinion)
> estudiantes
sexo puntuacion opinion
1 H 7.5 B
2 M 8.0 R
3 M 2.0 M
4 M 6.5 M
5 M 10.0 R
6 H 9.0 B
c) La puntuación media de los hombres y de las mujeres.
Para calcular las puntuaciones medias de hombres y mujeres tendremos en cuenta que hay 2 hombres en el fichero de datos, ocupando las posiciones 1 y 6 y que hay 4 mujeres en el fichero de datos, ocupando las posiciones 2, 3, 4 y 5.
>media_H<- (estudiantes$puntuacion[1] + estudiantes$puntuacion[6])/2
>media_M<- (estudiantes$puntuacion[2] + estudiantes$puntuacion[3]
+ + estudiantes$puntuacion[4] + estudiantes$puntuacion[5])/4
>media_H
[1] 8.25
>media_M
[1] 6.625
Resultando que la puntuación media de los hombres es mayor que la de las mujeres.
d) Los datos de las tres variables para el quinto individuo
>estudiantes[5,]
sexo puntuacionopinión
5 M 10 R
e) El logaritmo neperiano de la puntuación del tercer individuo
>log(estudiantes$puntuacion[3])
[1] 0.6931472
f) Comprobar si la puntuación del segundo individuo o del cuarto individuo es superior a 7
>estudiantes$puntuacion[2] > 7 | estudiantes$puntuacion[4] > 7
[1] TRUE
Ejercicios Propuestos
Ejercicio Propuesto 1
En la siguiente tabla se muestra la altura, en metros, de los pinos que componen 4 parcelas de terreno.
\( \begin{array} {|c|c|c|c|} \hline Parcela \hspace{.1cm} 1 & Parcela \hspace{.1cm} 2 & Parcela \hspace{.1cm} 3 & Parcela \hspace{.1cm} 4 \\ \hline 7.5 & 12.5 & 11 & 12.5 \\ \hline 12 & 10.5 & 8 & 16 \\ \hline 14.5 & 13 & 7.5 & 9.5 \\ \hline & 9 & 9.5 & 10 \\ \hline & 18.5 & 19 & \\ \hline & & 14 & \\ \hline \end{array} \)
Tabla 3. Datos del Ejercicio Propuesto 1
Se pide:
a) Crear 4 vectores numéricos, de manera que cada uno almacene la altura de los pinos de una parcela
b) Agrupar los 4 vectores creados en el apartado anterior en una estructura de datos adecuada, teniendo en cuenta sus características
c) Comprobar, para cada parcela, si la altura del primer pino supera a la del último pino
d) Calcular el logaritmo decimal de la altura del tercer pino de la parcela 3
e) Calcular la suma de las alturas de los 3 primeros pinos de la parcela 4
f) Obtener la altura media de los pinos de la parcela 1.
Ejercicio Propuesto 2
En la siguiente tabla se recoge información sobre el sexo, la tensión arterial y el pulso por minuto de los pacientes atendidos en una clínica a lo largo de un día
\( \begin{array} {|c|c|c|} \hline Sexo & Tensión \hspace{.1cm} arterial & Pulso \\ \hline Hombre & 119 & 59 \\ \hline Mujer & 99 & 89 \\ \hline Hombre & 102 & 107 \\ \hline Hombre & 78 & 76 \\ \hline Mujer & 78 & 91 \\ \hline \end{array} \)
Tabla 4. Datos del Ejercicio Propuesto 2
a) Elaborar un fichero de texto (con extensión .txt) que contenga la información de la tabla anterior. Utilizar el tabulador para separar la información referente a cada variable. Guárdalo en el escritorio y llamarlo salud.txt
b) Desde R leer el fichero que se acaba de crear y almacenar su contenido en una variable de nombre datos
c) Obtener los valores para las tres variables para el primer y el cuarto individuo
d) Comprobar si la primera mujer (posición 2) tiene una tensión arterial mayor que la segunda mujer (posición 5)
e) Calcular la media del pulso de los hombres
f ) Obtener la raíz cuadrada de la tensión arterial del cuarto individuo.
Ejercicio Propuesto 1 (Resuelto)
En la siguiente tabla se muestra la altura, en metros, de los pinos que componen 4 parcelas de terreno.
\( \begin{array} {|c|c|c|c|} \hline Parcela \hspace{.1cm} 1 & Parcela \hspace{.1cm} 2 & Parcela \hspace{.1cm} 3 & Parcela \hspace{.1cm} 4 \\ \hline 7.5 & 12.5 & 11 & 12.5 \\ \hline 12 & 10.5 & 8 & 16 \\ \hline 14.5 & 13 & 7.5 & 9.5 \\ \hline & 9 & 9.5 & 10 \\ \hline & 18.5 & 19 & \\ \hline & & 14 & \\ \hline \end{array} \)
Tabla 3. Datos del Ejercicio Propuesto 1
Se pide:
a) Crear 4 vectores numéricos, de manera que cada uno almacene la altura de los pinos de una parcela
> P1
[1] 7.5 12.0 14.0 5.0
> P2
[1] 12.5 10.5 13.0 9.0 18.5
> P3
[1] 11.0 8.0 7.5 9.5 19.0 14.0
> P4
[1] 12.5 16.0 9.5 10.0
b) Agrupar los 4 vectores creados en el apartado anterior en una estructura de datos adecuada, teniendo en cuenta sus características
> pinos
[[1]]
[1] 7.5 12.0 14.0 5.0
[[2]]
[1] 12.5 10.5 13.0 9.0 18.5
[[3]]
[1] 11.0 8.0 7.5 9.5 19.0 14.0
[[4]]
[1] 12.5 16.0 9.5 10.0
> pinos <- list(P1, P2, P3, P4)
c) Comprobar, para cada parcela, si la altura del primer pino supera a la del último pino
[1] FALSE
[1] FALSE
[1] FALSE
[1] TRUE
d) Calcular el logaritmo decimal de la altura del tercer pino de la parcela 3
[1] 0.8750613
e) Calcular la suma de las alturas de los 3 primeros pinos de la parcela 4
[1] 38
f) Obtener la altura media de los pinos de la parcela 1
[1] 11.16667
Ejercicio propuesto 1 (resuelto)
Ejercicio Propuesto 2 (Resuelto)
En la siguiente tabla se recoge información sobre el sexo, la tensión arterial y el pulso por minuto de los pacientes atendidos en una clínica a lo largo de un día
\( \begin{array} {|c|c|c|} \hline Sexo & Tensión \hspace{.1cm} arterial & Pulso \\ \hline Hombre & 119 & 59 \\ \hline Mujer & 99 & 89 \\ \hline Hombre & 102 & 107 \\ \hline Hombre & 78 & 76 \\ \hline Mujer & 78 & 91 \\ \hline \end{array} \)
Tabla 4. Datos del Ejercicio Propuesto 2
Se pide:
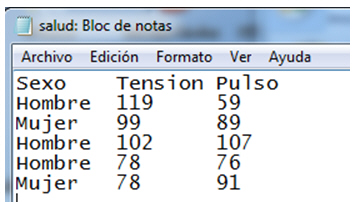
a) Elaborar un fichero de texto (con extensión .txt) que contenga la información de la tabla anterior. Utilizar el tabulador para separar la información referente a cada variable. Guárdalo en el escritorio y llamarlo salud.txt
b) Desde R leer el fichero que se acaba de crear y almacenar su contenido en una variable de nombre datos
>datos<- read.table(“salud.txt”, header = TRUE)
Nota: Utilizar la siguiente orden para situarse en el directorio de trabajo
> setwd(“C:/Users/Usuario/Desktop/nombrecarpeta”)
c) Obtener los valores para las 3 variables para el primer y el cuarto individuo
Sexo Tension Pulso
1 Hombre 119 59
4 Hombre 78 76
d) Comprobar si la primera mujer (posición 2) tiene una tensión arterial mayor que la segunda mujer (posición 5)
[1] TRUE
e) Calcular la media del pulso de los hombres
[1] 80.66667
f ) Obtener la raíz cuadrada de la tensión arterial del cuarto individuo.
[1] 8.831761
Ejercicio Propuesto 2 (Resuelto)
Autores: David Molina Muñoz, Ana María Lara Porras. Universidad de Granada y Rafael Cantos Villanueva (www.tiflocordoba.org) (2017)
Reformulado con MathML en 2021 por Ana María Lara Porras