DISEÑO ESTADÍSTICO DE EXPERIMENTOS
Objetivos
- Identificar un diseño unifactorial de efectos fijos.
- Plantear y resolver el contraste sobre las medias de los tratamientos.
- Saber aplicar los procedimientos de comparaciones múltiples.
- Identificar un diseño unifactorial de efectos aleatorios.
- Estimar los componentes de la varianza.
- Identificar un diseño en bloque completo aleatorizado con efectos fijos.
- Identificar un diseño en bloque incompleto aleatorizado con efectos fijos.
- Identificar un diseño en bloque incompleto balanceado (BIB).
- Identificar un diseño en cuadrados latinos.
- Identificar un diseño en cuadrados greco-latinos.
- Identificar un diseño en cuadrados de Jouden.
- Plantear y resolver los contrastes de igualdad de tratamientos y de igualdad de bloques.
- Identificar un diseño bifactorial de efectos fijos y estudiar las interacciones entre los factores.
- Identificar un diseño trifactorial de efectos fijos y estudiar las interacciones entre los factores
- Estudiar la influencia de los factores.
- Analizar en qué sentido se producen las interacciones mediante el gráfico de medias.
- Aplicar los procedimientos de comparaciones múltiples: Obtener conclusiones sobre el experimento planteado y las interacciones.
- Analizar la idoneidad de los modelos planteados.
Introducción al Diseño Estadístico de Experimentos
En la práctica 6 hemos descrito métodos de inferencias sobre la media y la varianza de una población y de dos poblaciones. En esta práctica 7 ampliamos dichos métodos a más de dos poblaciones e introducimos algunos aspectos elementales del Diseño Estadístico de Experimentos y del Análisis de la Varianza.
El diseño estadístico de experimentos incluye un conjunto de técnicas de análisis y un método de construcción de modelos estadísticos que, conjuntamente, permiten llevar a cabo el proceso completo de planificar un experimento para obtener datos apropiados, que puedan ser analizados con métodos estadísticos, con objeto de obtener conclusiones válidas y objetivas.
El análisis de la varianza o abreviadamente ANOVA (del inglés analysis of variance) es un procedimiento estadístico que permite dividir la variabilidad observada en componentes independientes que pueden atribuirse a diferentes causas de interés. Es una técnica estadística para comparar más de dos grupos, es decir un método para comparar más de dos tratamientos y la variable de estudio o variable respuesta es numérica.
En esta práctica presentamos el Diseño Completamente Aleatorio con efectos fijos y con efectos aleatorios, el Diseño en Bloques Completos Aleatorizados, Diseño en Bloques Incompletos Balanceados (BIB), el Diseño en Cuadrados Latinos, el Diseño en Cuadrados Greco-Latinos, el Diseño en Cuadrados de Jouden, el Diseño Bifactorial de efectos fijos y el Diseño Trifactorial de efectos fijos.
Diseño Completamente Aleatorio con efectos fijos (Diseño unifactorial de efectos fijos)
El primer diseño que presentamos es el diseño completamente aleatorio de efectos fijos y la técnica estadística es el análisis de la varianza de una vía o un factor. La descripción del diseño así como la terminología subyacente la vamos a introducir mediante el siguiente supuesto práctico.
Supuesto práctico 1
La contaminación es uno de los problemas ambientales más importantes que afectan a nuestro mundo. En las grandes ciudades, la contaminación del aire se debe a los escapes de gases de los motores de explosión, a los aparatos domésticos de la calefacción, a las industrias,… El aire contaminado nos afecta en nuestro vivir diario, manifestándose de diferentes formas en nuestro organismo. Con objeto de comprobar la contaminación del aire en una determinada ciudad, se ha realizado un estudio en el que se han analizado las concentraciones de monóxido de carbono (CO) durante cinco días de la semana (lunes, martes, miércoles, jueves y viernes).
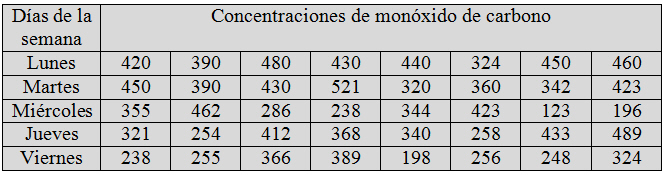
Figura1: Tabla de datos del Supuesto Práctico1
En el ejemplo disponemos de una colección de 40 unidades experimentales y queremos estudiar el efecto de las concentraciones de monóxido de carbono en 5 días distintos. Es decir, estamos interesados en contrastar el efecto de un solo factor, que se presenta con cinco niveles, sobre la variable respuesta.
Nos interesa saber si las concentraciones medias de monóxido de carbono son iguales en los cinco días de la semana, para ello realizamos el siguiente contraste de hipótesis:
![]() Expresión 1: Contraste de hipótesis
Expresión 1: Contraste de hipótesis
Es decir, contrastamos que no hay diferencia en las medias de los cinco tratamientos frente a la alternativa de que al menos una media difiere de otra.
En este modelo, que estudia el efecto que produce un solo factor en la variable respuesta, la asignación de las unidades experimentales a los distintos niveles del factor se debe realizar de forma completamente al azar. Este modelo, junto con este procedimiento de asignación, recibe el nombre de Diseño Completamente Aleatorizado y está basado en el modelo estadístico de Análisis de la Varianza de un Factor o una Vía. Esta técnica estadística, Análisis de la Varianza de un factor, se utiliza cuando se tienen que comparar más de dos grupos y la variable respuesta es una variable numérica. Para aplicar este diseño adecuadamente las unidades experimentales deben ser lo más homogéneas posible.
Todo este planteamiento se puede formalizar de manera general para cualquier experimento unifactorial. Supongamos un factor con I niveles y para el nivel i-ésimo se obtienen ni observaciones de la variable respuesta. Entonces podemos postular el siguiente modelo:
![]() Expresión 2: Ecuación del modelo unifactorial
Expresión 2: Ecuación del modelo unifactorial
donde:
- yij: es la variable aleatoria que representa la observación j-ésima del i-ésimo tratamiento (Variable respuesta).
- µ: Es un efecto constante, común a todos los niveles del factor, denominado media global.
- τi: es la parte de yij debida a la acción del nivel i-ésimo, que será común a todos los elementos sometidos a ese nivel del factor, llamado efecto del tratamiento i-ésimo.
- uij: son variables aleatorias que engloban un conjunto de factores, cada uno de los cuales influye en la respuesta sólo en pequeña magnitud pero que de forma conjunta debe tenerse en cuenta. Es decir, se pueden interpretar como las variaciones causadas por todos los factores no analizados y que dentro del mismo tratamiento variarán de unos elementos a otros. Reciben el nombre de perturbaciones o error experimental.
Nuestro objetivo es estimar el efecto de los tratamientos y contrastar la hipótesis de que todos los niveles del factor producen el mismo efecto, frente a la alternativa de que al menos dos difieren entre sí. Para ello, se supone que los errores experimentales son variables aleatorias independientes igualmente distribuidas según una Normal de media cero y varianza constante.
En este modelo se distinguen dos situaciones según la selección de los tratamientos: modelo de efectos fijos y modelo de efectos aleatorios.
En el modelo de efectos fijos el experimentador decide qué niveles concretos se van a considerar y las conclusiones que se obtengan sólo son aplicables a esos niveles, no pudiéndose hacer extensivas a otros niveles no incluidos en el estudio.
En el modelo de efectos aleatorios, los niveles del factor se seleccionan al azar; es decir los niveles estudiados son una muestra aleatoria de una población de niveles y las conclusiones que se obtengan se generalizan a todos los posibles niveles del factor, hayan sido explícitamente considerados en el estudio o no.
En cuanto a los tamaños muestrales de los tratamientos, los modelos se clasifican en: modelo equilibrado o balanceado si todas las muestras son del mismo tamaño ni = n y modelo no-equilibrado o no-balanceado si los tamaños muestrales ni son distintos.
El contraste de hipótesis planteado anteriormente está asociado a la descomposición de la variabilidad de la variable respuesta. Dicha variabilidad se descompone de la siguiente forma:
SCT = SCTr + SCR
Donde:
SCT: es la suma de cuadrados total o variabilidad total de Y
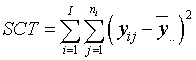 Expresión 3: Suma de cuadrados Total
Expresión 3: Suma de cuadrados Total
SCTr: es la suma de cuadrados entre tratamientos o variabilidad explicada,
 Expresión 4: Suma de cuadrados entre Tratamientos
Expresión 4: Suma de cuadrados entre Tratamientos
SCR: es la suma de cuadrados dentro de los tratamientos, variabilidad no explicada o residual
![]() Expresión 5: Suma de cuadrados Residual
Expresión 5: Suma de cuadrados Residual
La tabla de análisis de la varianza (tabla ANOVA) se construye a partir de esta descomposición y proporciona el valor del estadístico F que permite contrastar la hipótesis nula planteada anteriormente.
![]() Expresión 1: Contraste de hipótesis
Expresión 1: Contraste de hipótesis
En el Supuesto práctico 1:
- Variable respuesta: Concentración de CO.
- Factor: Día de la semana que tiene cinco niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar (5 días de la semana).
- Modelo equilibrado: Los niveles de los factores tienen el mismo número de elementos (8 elementos).
- Tamaño del experimento: Número total de observaciones, en este caso 40 unidades experimentales.
El problema planteado se modeliza a través de un diseño unifactorial totalmente aleatorizado de efectos fijos equilibrado.
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos realizarlo directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto: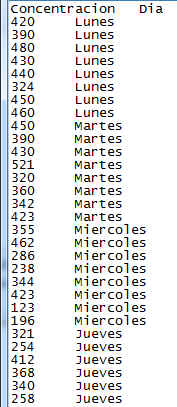
Figura 2: Tabla de datos del Supuesto práctico 1
En primer lugar describimos los cinco grupos que tenemos que comparar, los cinco días de la semana, la variable respuesta es la concentración de CO en estos días de la semana. Cada día de la semana tiene ocho unidades, en total tenemos 40 observaciones. La hipótesis nula es que el promedio de las concentraciones es igual el día lunes que el martes, que el miércoles… Es decir, no hay diferencias en las concentraciones con respecto a los días y la alternativa es que las concentraciones de CO son diferentes al menos en dos días.
Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en Figura 1, es decir, las observaciones en una sola columna y a continuación especificado su tratamiento y su bloque correspondiente.
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
Nota: La ruta hasta llegar al fichero varía en función del ordenador. Utilizar la orden setwd() para situarse en el directorio de trabajo
> setwd(“C:/Users/Usuario/Desktop/Datos”)
> contaminacion <- read.table(“supuesto1.txt”, header = TRUE)
> contaminacion
Concentracion Dia
1 420 Lunes
2 390 Lunes
3 480 Lunes
4 430 Lunes
5 440 Lunes
6 324 Lunes
7 450 Lunes
8 460 Lunes
9 450 Martes
10 390 Martes
11 430 Martes
12 521 Martes
13 320 Martes
Se puede realizar de dos formas:
- Transformar la variable referente a los niveles del factor fijo como factor
> contaminacion$dia<-factor(contaminacion$Dia)
> contaminacion$dia
[1] Lunes Lunes Lunes Lunes Lunes Lunes Lunes
[8] Lunes Martes Martes Martes Martes Martes Martes
[15] Martes Martes Miercoles Miercoles Miercoles Miercoles Miercoles
[22] Miercoles Miercoles Miercoles Jueves Jueves Jueves Jueves
[29] Jueves Jueves Jueves Jueves Viernes Viernes Viernes
[36] Viernes Viernes Viernes Viernes Viernes
Levels: Jueves Lunes Martes Miercoles Viernes
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
> mod <- aov(Concentracion ~ Dia, data = contaminacion)
donde:
- Concentracion = nombre de la columna de las observaciones.
- Dia = nombre de la columna en la que están representados los tratamientos.
- data= data.frame en el que están guardados los datos.
> mod <- aov(Concentracion ~ Dia, data = contaminacion)
> mod
Call:
aov(formula = Concentracion ~ Dia, data = contaminacion)
Terms:
Dia Residuals
Sum of Squares 119484.4 218948.8
Deg. of Freedom 4 35
Residual standard error: 79.09285
Estimated effects may be unbalanced
Se puede mostrar un resumen de los resultados con la función “summary” (verdadera tabla ANOVA)
> summary(mod) # TABLA ANOVA
Df Sum Sq Mean Sq F value Pr(>F)
Dia 4 119484 29871 4.775 0.00352 **
Residuals 35 218949 6256
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Si el valor de F es mayor que uno quiere decir que hay un efecto positivo del factor día. Se observa que el P-valor (Sig.) tiene un valor de 0.003524, que es menor que el nivel de significación 0.05. Por lo tanto, hemos comprobado estadísticamente que estos cinco grupos son distintos. Es decir, existen diferencias significativas en las concentraciones medias de monóxido de carbono entre los cinco días de la semana. Por lo tanto no se puede rechazar la hipótesis alternativa que dice que al menos dos grupos son diferentes, pero ¿Cuáles son esos grupos? ¿Los cinco grupos son distintos o sólo alguno de ellos? Pregunta que resolveremos más adelante mediante los contrastes de comparaciones múltiples.
2. En la expresión del comando “aov” indicar el factor
> mod1 <- aov(Concentracion ~ factor (Dia), data = contaminacion)
> mod1
Call:
aov(formula = Concentracion ~ factor(Dia), data = contaminacion)
Terms:
factor(Dia) Residuals
Sum of Squares 119484.4 218948.8
Deg. of Freedom 4 35
Residual standard error: 79.09285
Estimated effects may be unbalanced
> summary(mod1)
Df Sum Sq Mean Sq F value Pr(>F)
factor(Dia) 4 119484 29871 4.775 0.00352 **
Residuals 35 218949 6256
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
También se puede utilizar el comando “anova” y no es necesario el comando “summary”
> mod2 <- anova (lm (Concentracion ~ factor (Dia), data = contaminacion))
> mod2
Analysis of Variance Table
Response: Concentracion
Df Sum Sq Mean Sq F value Pr(>F)
factor(Dia) 4 119484 29871.1 4.775 0.003518 **
Residuals 35 218949 6255.7
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Los datos pueden venir dados en diferentes formatos:
1. Caso en el que los datos se muestran de forma que se analiza la contaminación con cada uno de los dias de la semana (de lunes a viernes). Como se muestra a continuación
> contaminacion <- read.table(“supuesto1-1.txt”, header = TRUE)
> contaminacion
Lunes Martes Miercoles Jueves Viernes
1 420 450 355 321 238
2 390 390 462 254 255
3 480 430 286 412 366
4 430 521 238 368 389
5 440 320 344 340 198
6 324 360 423 258 256
7 450 342 123 433 248
8 460 423 196 489 324
En primer lugar apilaremos las columnas, para ello utilizamos el comando “stack” de la siguiente forma
> trats <- stack(contaminacion)
> trats
values ind
1 420 Lunes
2 390 Lunes
3 480 Lunes
4 430 Lunes
5 440 Lunes
6 324 Lunes
7 450 Lunes
8 460 Lunes
9 450 Martes
10 390 Martes
11 430 Martes
12 521 Martes
13 320 Martes
14 360 Martes
15 342 Martes
16 423 Martes
17 355 Miercoles
18 462 Miercoles
19 286 Miercoles
20 238 Miercoles
21 344 Miercoles
22 423 Miercoles
23 123 Miercoles
24 196 Miercoles
25 321 Jueves
26 254 Jueves
27 412 Jueves
28 368 Jueves
29 340 Jueves
30 258 Jueves
31 433 Jueves
32 489 Jueves
33 238 Viernes
34 255 Viernes
35 366 Viernes
36 389 Viernes
37 198 Viernes
38 256 Viernes
39 248 Viernes
40 324 Viernes
Nos muestra dos columnas:
- La primera columna: values nos muestra los valores de la variable respuesta. En este caso la contaminación
- La segunda columna: ind nos muestra los diferentes tratamientos
Podemos realizar el Análisis de la varianza utilzando el comando anova
> anova(lm(values ~ ind, data = trats))
Analysis of Variance Table
Response: values
Df Sum Sq Mean Sq F value Pr(>F)
ind 4 119484 29871.1 4.775 0.003518 **
Residuals 35 218949 6255.7
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
2. Los datos vienen dados de la siguiente forma:
Lunes: 420, 390, 480, 430, 440, 324, 450, 460
Martes: 450, 390, 430, 521, 320, 360, 342, 423
Miércoles: 355, 462, 286, 238, 344, 423, 123, 196
Jueves: 321, 254, 412, 368, 340, 258, 433, 489
Viernes: 238, 255, 366, 389, 198, 256, 248, 324
Se crean cinco vectores, cada uno de ellos representando la contaminación con un tratamiento.
> Lu= c(420, 390, 480, 430, 440, 324, 450, 460)
> Ma = c(450, 390, 430, 521, 320, 360, 342, 423)
> Mi= c(355, 462, 286, 238, 344, 423, 123, 196)
> Ju=c(321, 254, 412, 368, 340, 258, 433, 489)
> Vi= c(238, 255, 366, 389, 198, 256, 248, 324)
> Lu
[1] 420 390 480 430 440 324 450 460
> Ma
[1] 450 390 430 521 320 360 342 423
> Mi
[1] 355 462 286 238 344 423 123 196
> Ju
[1] 321 254 412 368 340 258 433 489
> Vi
[1] 238 255 366 389 198 256 248 324
Acontinuación creamos un data.frame para poder resolver el ANOVA
> datos = data.frame(Lu, Ma, Mi, Ju,Vi)
> datos
Lu Ma Mi Ju Vi
1 420 450 355 321 238
2 390 390 462 254 255
3 480 430 286 412 366
4 430 521 238 368 389
5 440 320 344 340 198
6 324 360 423 258 256
7 450 342 123 433 248
8 460 423 196 489 324
De esta forma hemos creado una nueva base de datos que hemos llamado “datos“. Para resolver el ANOVA tenemos primero que apilar las columnas con el comando “stack”
> datos1 = stack(datos)
> datos1
values ind
1 420 Lu
2 390 Lu
3 480 Lu
4 430 Lu
5 440 Lu
6 324 Lu
7 450 Lu
8 460 Lu
9 450 Ma
10 390 Ma
11 430 Ma
12 521 Ma
13 320 Ma
14 360 Ma
15 342 Ma
16 423 Ma
17 355 Mi
18 462 Mi
19 286 Mi
20 238 Mi
21 344 Mi
22 423 Mi
23 123 Mi
24 196 Mi
25 321 Ju
26 254 Ju
27 412 Ju
28 368 Ju
29 340 Ju
30 258 Ju
31 433 Ju
32 489 Ju
33 238 Vi
34 255 Vi
35 366 Vi
36 389 Vi
37 198 Vi
38 256 Vi
39 248 Vi
40 324 Vi
Resolvemos el ANOVA como en el caso anterior
> anova(lm(values ~ ind, data = datos1))
Analysis of Variance Table
Response: values
Df Sum Sq Mean Sq F value Pr(>F)
ind 4 119484 29871.1 4.775 0.003518 **
Residuals 35 218949 6255.7
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
3. Los datos se muestren en un solo vector que tiene todos los datos de la contaminación tanto si se ha medido el lunes, el martes, el miércoles, el jueves o el viernes
> contaminacion = c(Lu, Ma, Mi, Ju, Vi)
> contaminacion
[1] 420 390 480 430 440 324 450 460 450 390 430 521 320 360 342 423 355 462 286
[20] 238 344 423 123 196 321 254 412 368 340 258 433 489 238 255 366 389 198 256
[39] 248 324
Este vector esta formado por los 40 datos que podemos comprobarlo con el comando length
> length(contaminacion)
[1] 40
Para realizar el ANOVA, ya tenemos los datos de la variable respuesta y a continuación tenemos que crear el factor tratamiento, para ello vamos a utilizar la función generador de niveles, gl, y le decimos que nos genere 5 niveles que son los cinco tratamientos, cada uno repetido 8 veves con un total de 40 datos y para identificar que nivel es cada uno, creamos las etiquetas L, M, Mi, J y V
> trat = gl(5,8,40, labels= c (“L”, “M”, “Mi”, “j”, “V”))
> trat
[1] L L L L L L L L M M M M M M M M Mi Mi Mi Mi Mi Mi Mi Mi j
[26] j j j j j j j V V V V V V V V
Levels: L M Mi j V
> anova(lm(contaminacion~trat))
Analysis of Variance Table
Response: contaminacion
Df Sum Sq Mean Sq F value Pr(>F)
trat 4 119484 29871.1 4.775 0.003518 **
Residuals 35 218949 6255.7
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
El modelo que hemos propuesto hay que validarlo, para ello hay que comprobar si se verifican las hipótesis básicas del modelo, es decir, si las perturbaciones son variables aleatorias independientes con distribución normal de media 0 y varianza constante (homocedasticidad).
Estudio de la Idoneidad del modelo
Como hemos dicho anteriormente, validar el modelo propuesto consiste en estudiar si las hipótesis básicas del modelo están o no en contradicción con los datos observados. Es decir si se satisfacen los supuestos del modelo: Normalidad, Independencia, Homocedasticidad. Para ello utilizamos procedimientos gráficos y analíticos.
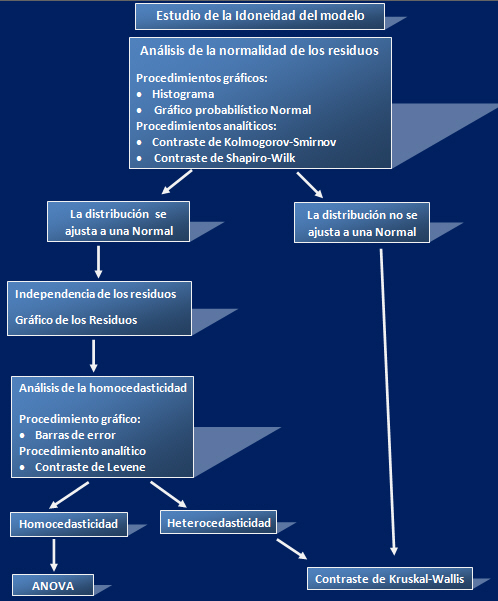 Figura 3: Estudio de la Idoneidad del modelo
Figura 3: Estudio de la Idoneidad del modelo
Hipótesis de normalidad
En primer lugar, analizamos la normalidad de las concentraciones y continuamos con el análisis de la normalidad de los residuos.
Para analizar la normalidad de las concentraciones utilizamos el test de Shapiro-Wilks
> shapiro.test(mod$residuals)
Shapiro-Wilk normality test
data: mod$residuals
W = 0.98933, p-value = 0.9654
Observamos el contraste de Shapiro-Wilk que es adecuado cuando las muestras son pequeñas (n < 50) y es una alternativa más potente que el test de Kolmogorov-Smirnov. El p-valor es mayor que el nivel de significación del 5%, concluyendo que las muestras de las concentraciones se distribuyen de forma normal en cada día de la semana.
Podemos verlo también gráficamente con la orden “qqnorm”
> qqnorm (mod$residuals)
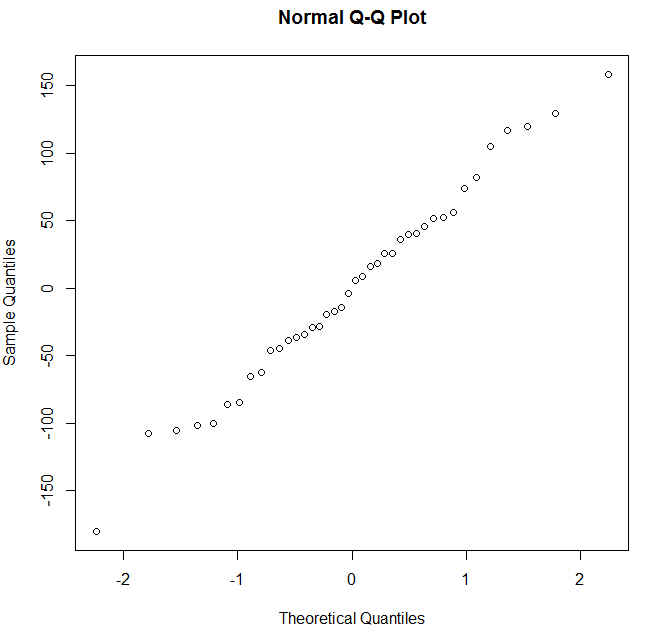
Podemos apreciar en este gráfico que los puntos aparecen próximos a la línea diagonal. Esta gráfica no muestra una desviación marcada de la normalidad.
Hipótesis de homocedasticidad
Para comprobar la hipótesis de igualdad entre las varianzas del factor utilizamos el Test de Barlett.
> bartlett.test(contaminacion$Concentracion, contaminacion$Dia)
Bartlett test of homogeneity of variances
data: contaminacion$Concentracion and contaminacion$Dia
Bartlett’s K-squared = 5.4942, df = 4, p-value = 0.2402
El p-valor es del 0.2402 que al ser mayor del nivel significación usual del 5% no podemos rechazar la hipótesis de igualdad de varianzas, es decir, se acepta la igualdad de varianzas en el factor.
Hipótesis de independencia
Para comprobar que se satisface el supuesto de independencia entre los residuos analizamos el gráfico de los residuos frente a los valores pronosticados o predichos por el modelo. El empleo de este gráfico es útil puesto que la presencia de alguna tendencia en el mismo puede ser indicio de una violación de dicha hipótesis. En R obtenemos varios gráficos a la vez que están incluidos en la estimación del modelo.
Para verlos de forma correcta hacemos uso de las siguientes órdenes:
> layout(matrix(c(1,2,3,4),2,2)) # para que salgan en la misma pantalla
> plot(mod)
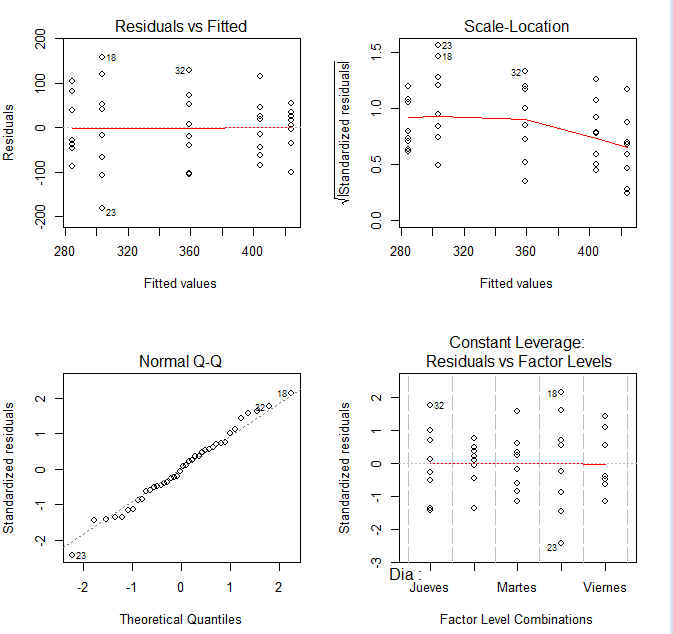 Figura 5: Estudio gráfico de la hipótesis de independencia
Figura 5: Estudio gráfico de la hipótesis de independencia
En la Figura 5 se muestran cuatro gráficos, en el primero de ellos que se representan los residuos en el eje de ordenadas y los valores pronosticados en el eje de abscisas. No observamos, en dicho gráfico, ninguna tendencia sistemática que haga sospechar del incumplimiento de la suposición de independencia.
Anteriormente, hemos comprobado estadísticamente que estos cinco grupos son distintos. Es decir no se puede rechazar la hipótesis alternativa que dice que al menos dos grupos son diferentes, pero ¿Cuáles son esos grupos? ¿Los cinco grupos son distintos o sólo alguno de ellos? Pregunta que resolveremos más adelante mediante los contrastes de comparaciones múltiples.
Comparaciones múltiples
Para saber entre que parejas de días las diferencias entre concentraciones medias de CO son significativas aplicamos la prueba Post-hoc de Tukey
> mod.tukey<- TukeyHSD(mod, ordered = TRUE)
> mod.tukey
Tukey multiple comparisons of means
95% family-wise confidence level
factor levels have been ordered
Fit: aov(formula = Concentracion ~ Dia, data = contaminacion)
$Dia
diff lwr upr p adj
Miercoles-Viernes 19.125 -94.573356 132.8234 0.9883811
Jueves-Viernes 75.125 -38.573356 188.8234 0.3363682
Martes-Viernes 120.250 6.551644 233.9484 0.0337946
Lunes-Viernes 140.000 26.301644 253.6984 0.0095230
Jueves-Miercoles 56.000 -57.698356 169.6984 0.6217479
Martes-Miercoles 101.125 -12.573356 214.8234 0.1010091
Lunes-Miercoles 120.875 7.176644 234.5734 0.0325284
Martes-Jueves 45.125 -68.573356 158.8234 0.7837763
Lunes-Jueves 64.875 -48.823356 178.5734 0.4826413
Lunes-Martes 19.750 -93.948356 133.4484 0.9868896
Esta salida nos muestra los intervalos de confianza simultáneos construidos por el método de Tukey. En la tabla se muestra un resumen de las comparaciones de cada tratamiento con los restantes. Es decir, aparecen comparadas dos a dos las cinco medias de los tratamientos.
En esta tabla, las columnas:
- diff: muestra las medias de cada par
- p adj: muestra los p-valores de los contrastes, que permiten conocer si la diferencia entre cada pareja de medias es significativa al nivel de significación considerado (en este caso 0.05)
- lwr y upr: proporcionan los intervalos de confianza al 95% para cada diferencia.
Así por ejemplo, si comparamos la concentración media de CO del Lunes con el Martes, tenemos una diferencia entre ambas medias de 19.750, un p-valor (Sig.) de 0.9868896 no significativo puesto que la concentración de CO no difiere significativamente el lunes del martes y un intervalo de confianza con un límite inferior negativo y un límite superior positivo y por lo tanto contiene al cero de lo que también deducimos que no hay diferencias significativas entre los dos grupos que se comparan o que ambos grupos son homogéneos.
En cambio si observamos el grupo formado por el Lunes y el Miércoles, vemos que ambos extremos del intervalo son del mismo signo y el p-valor es significativo deduciendo que si hay diferencias significativas entre ambos. Las otras comparaciones se interpretan de forma análoga.
Por lo tanto la tabla se interpreta observando los valores de p adj menores que el 5%, o si el intervalo de confianza contiene al cero.
Concluimos que se detectan diferencias significativas en las concentraciones de CO entre lunes y miércoles; lunes y viernes; martes y viernes.
Diseño Unifactorial de efectos aleatorios
En el modelo de efectos aleatorios, los niveles del factor son una muestra aleatoria de una población de niveles. Este modelo surge ante la necesidad de estudiar un factor que presenta un número elevado de posibles niveles, que en algunas ocasiones puede ser infinito. En este modelo las conclusiones obtenidas se generalizan a toda la población de niveles del factor, ya que los niveles empleados en el experimento fueron seleccionados al azar. El estudio de este diseño lo vamos a realizar mediante el siguiente supuesto práctico.
Supuesto práctico 2
Los medios de cultivo bacteriológico en los laboratorios de los hospitales proceden de diversos fabricantes. Se sospecha que la calidad de estos medios de cultivo varía de un fabricante a otro. Para comprobar esta teoría, se hace una lista de fabricantes de un medio de cultivo concreto, se seleccionan aleatoriamente los nombres de cinco de los que aparecen en la lista y se comparan las muestras de los instrumentos procedentes de éstos. La comprobación se realiza colocando sobre una placa dos dosis, en gotas, de una suspensión medida de un microorganismo clásico, Escherichia coli, dejando al cultivo crecer durante veinticuatro horas, y determinando después el número de colonias (en millares) del microorganismo que aparecen al final del período. Se quiere comprobar si la calidad del instrumental difiere entre fabricantes.
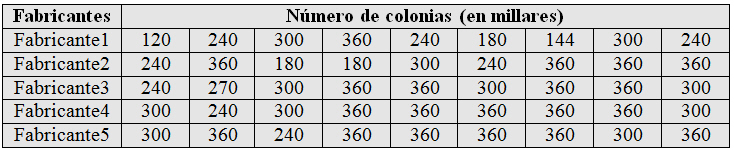 Figura 6: Tabla de datos del Supuesto práctico 2.txt
Figura 6: Tabla de datos del Supuesto práctico 2.txt
Supuestos del modelo
-
Las cinco muestras representan muestras aleatorias independientes extraídas de I poblaciones seleccionadas aleatoriamente de un conjunto mayor de poblaciones.
-
Todas las poblaciones del conjunto más amplio tienen distribución Normal, de modo que cada una de las 5 poblaciones muestreadas se distribuyen según una Normal
-
Todas las poblaciones del conjunto más amplio tienen la misma varianza, y por lo tanto, cada una de las 5 poblaciones muestreadas tiene también varianza σ2.
El modelo matemático de este diseño y los tres primeros supuestos del modelo son semejantes a los del modelo de efectos fijos. Sin embargo, el supuesto 4 expresa matemáticamente una importante diferencia entre los dos. En el modelo de efectos fijos, el experimentador elige los tratamientos o niveles del factor utilizados en el experimento. Si se replicase el experimento, se utilizarían los mismos tratamientos. Es decir, se muestrearían las mismas poblaciones cada vez y los I efectos del tratamiento τi = μi – μ no variarían. Esto implica que en el modelo de efectos fijos, estos I términos se consideran constantes desconocidas. En el modelo de efectos aleatorios se seleccionan aleatoriamente I poblaciones, las elegidas variarán de replicación en replicación. De este modo, en este modelo los I términos μi – μ no son constantes, son variables aleatorias, cuyos valores para una determinada réplica depende de la elección de las I poblaciones a estudiar. En este modelo estas variables τi se suponen variables aleatorias normales independientes con media 0 y varianza común ![]() . Además este modelo requiere que las variables τi y uij sean independientes. Así, por la independencia de estas variables, la varianza de cualquier observación de la muestra, es decir, la varianza total, vale
. Además este modelo requiere que las variables τi y uij sean independientes. Así, por la independencia de estas variables, la varianza de cualquier observación de la muestra, es decir, la varianza total, vale
Expresión 6: Expresión de la Varianza total
La mecánica del Análisis de la Varianza es la misma que en el modelo de efectos fijos. En este modelo, carece de sentido probar la hipótesis que se refiere a los efectos de los tratamientos individuales. Si las medias poblacionales en el conjunto mayor son iguales, no variarán los efectos del tratamiento τi, es decir, ![]() . Así en el modelo de efectos aleatorios, la hipótesis de medias iguales se contrasta considerando:
. Así en el modelo de efectos aleatorios, la hipótesis de medias iguales se contrasta considerando:
![]() Expresión 7: Contraste de Hipótesis de la varianza total
Expresión 7: Contraste de Hipótesis de la varianza total
Si no se rechaza H0, significa que no hay variedad en los efectos de los tratamientos.
En el supuesto práctico 2:
- Variable respuesta: Calidad_Instrumental
- Factor: Fabricante. Es un factor de efectos aleatorios, se han elegido aleatoriamente a cinco fabricantes, que constituyen únicamente una muestra de todos los fabricantes y el propósito no es comparar estos cinco fabricantes sino contrastar el supuesto general de que la calidad del instrumental difiere entre fabricantes.
- Modelo equilibrado: Los niveles de los factores tienen el mismo número de elementos (9 elementos).
- Tamaño del experimento: Número total de observaciones, en este caso 45 unidades experimentales.
El problema planteado se modeliza a través de un diseño unifactorial totalmente aleatorizado de efectos aleatorios equilibrado.
Nota: La ruta hasta llegar al fichero varía en función del ordenador. Utilizar la orden setwd() para situarse en el directorio de trabajo
> setwd(“F:/Desktop/Datos”)
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto:
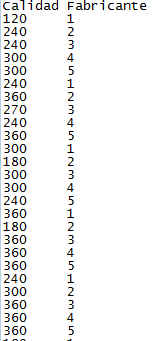
Figura 7 : Tabla de datos del Supuesto práctico 2.txt
Se quiere comprobar si la calidad del instrumental difiere entre fabricantes.
Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en la imagen, es decir, las observaciones en una sola columna y a continuación especificado su tratamiento y su bloque correspondiente.
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
> bacterias<-read.table(“supuesto2.txt”, header = TRUE)
> bacterias
Calidad Fabricante
1 120 1
2 240 2
3 240 3
4 300 4
5 300 5
6 240 1
7 360 2
8 270 3
9 240 4
10 360 5
11 300 1
12 180 2
13 300 3
14 300 4
Debemos transformar la variable referente a los niveles del factor fijo como factor para poder hacer los cálculos de forma adecuada
> bacterias$Fabricante<- factor(bacterias$Fabricante)
> bacterias$Fabricante
[1] 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3
[39] 4 5 1 2 3 4 5
Levels: 1 2 3 4 5
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
> mod <- aov(Calidad ~ Fabricante, data = bacterias)
donde:
- Calidad = nombre de la columna de las observaciones.
- Fabricante =nombre de la columna en la que están representados los tratamientos.
- data = data.frame en el que están guardados los datos.
> mod
Call:
aov(formula = Calidad ~ Fabricante, data = bacterias)
Terms:
Fabricante Residuals
Sum of Squares 57363.2 144272.0
Deg. of Freedom 4 40
Residual standard error: 60.05664
Estimated effects may be unbalanced
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
> summary(mod) # TABLA ANOVA
Df Sum Sq Mean Sq F value Pr(>F)
Fabricante 4 57363 14341 3.976 0.00827 **
Residuals 40 144272 3607
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Esta tabla muestra los resultados del contraste planteado. El valor del estadístico de contraste es igual a 3.976 que deja a la derecha un p-valor de 0.00827, así que la respuesta dependerá del nivel de significación que se fije. Si fijamos un nivel de significación de 0.05 se concluye que hay evidencia suficiente para afirmar la existencia de alguna variabilidad entre la calidad del material de los diferentes fabricantes. Si fijamos un nivel de significación de 0.001, no podemos hacer tal afirmación.
En el modelo de efectos aleatorios no se necesitan llevar a cabo más contrastes incluso aunque la hipótesis nula sea rechazada. Es decir, en el caso de rechazar \( H_0 \) no hay que realizar comparaciones múltiples para comprobar que medias son distintas, ya que el propósito del experimento es hacer un planteamiento general relativo a las poblaciones de las que se extraen las muestras.
En este caso, R no tiene ninguna función que nos permita calcular la varianza de tratamientos, por lo que tenemos que calcularla a mano:
En el modelo de efectos aleatorios las variables \( τ_{i} \) y \( u_{ij} \) son independientes, por lo tanto la varianza de cualquier observación de la muestra, es decir, la varianza total, vale
\( \sigma^{2}_{T} = \sigma_{\tau}^{2} + \sigma^{2} \)
Expresión 6: Expresión de la Varianza total
- Varianza dentro de los factores (Varianza residual)
\( \widehat{\sigma}^{2} = S^{2}_{R} = 3607 \)
Expresión 8: Valor de la Varianza residual
- Varianza entre los factores
\( \widehat { \sigma}_{\tau}^{2} = \displaystyle \frac {N \times (I-1)}{N^{2}- \sum_i n_{i}^{2}} (S^{2}_{Tr}-S^{2}_{R} ) = \displaystyle \frac {45 \times 4}{45^{2}-5 \times 9^{2}} (14341-3067) = 1192.667 \)
Expresión 9: Cálculo de la Varianza entre los factores
- Varianza Total
\( \widehat {\sigma}^{2}_{T} = \widehat {\sigma}_{\tau}^{2} + \widehat {\sigma}^{2}= 3607 + 1192.667 = 4799.667 \)
Expresión 10: Cálculo de la Varianza Total
Por lo tanto, la varianza total (4799.467) se descompone en una parte atribuible a la diferencia entre los fabricantes (1192.667) y otra procedente de la variabilidad existente dentro de ellos (3606.8). Comprobamos que en dicha varianza tiene mayor peso la variación dentro de los fabricantes, en porcentaje un 75.15 % frente a la variación entre fabricantes, que representa el 24.85 % del total.
Diseño en Bloques Aleatorizados
En los diseños estudiados anteriormente hemos supuesto que existe bastante homogeneidad entre las unidades experimentales. Pero puede suceder que dichas unidades experimentales sean heterogéneas y contribuyan a la variabilidad observada en la variable respuesta. Si en esta situación se utiliza un diseño completamente aleatorizado, no sabremos si la diferencia entre dos unidades experimentales sometidas a distintos tratamientos se debe a una diferencia real entre los efectos de los tratamientos o a la heterogeneidad de dichas unidades. Como resultado, el error experimental reflejará esta variabilidad. En esta situación se debe sustraer del error experimental la variabilidad producida por las unidades experimentales y para ello el experimentador puede formar bloques de manera que las unidades experimentales de cada bloque sean lo más homogéneas posible y los bloques entre sí sean heterogéneos.
En el diseño en bloques Aleatorizados, primero se clasifican las unidades experimentales en grupos homogéneos, llamados bloques, y los tratamientos son entonces asignados aleatoriamente dentro de los bloques. Esta estrategia de diseño mejora efectivamente la precisión en las comparaciones al reducir la variabilidad residual.
Distinguimos dos tipos de diseños en bloques aleatorizados:
- Los diseños en bloques completos aleatorizados (Todos los tratamientos se prueban en cada bloque exactamente vez).
- Los diseños por bloques incompletos aleatorizados (Todos los tratamientos no están representados en cada bloque, y aquellos que sí están en uno en particular se ensayan en él una sola vez).
Diseño en Bloques Completos Aleatorizados
En esta sección presentamos el diseño en Bloques Completos Aleatorizados. La palabra bloque se refiere al hecho de que se ha agrupado a las unidades experimentales en función de alguna variable extraña; aleatorizado se refiere al hecho de que los tratamientos se asignan aleatoriamente dentro de los bloques; completo implica que se utiliza cada tratamiento exactamente una vez dentro de cada bloque y el término efectos fijos se aplica a bloques y tratamientos. Es decir, se supone que ni los bloques ni los tratamientos se eligen aleatoriamente. Además una caracterización de este diseño es que los efectos bloque y tratamiento son aditivos; es decir no hay interacción entre los bloques y los tratamientos.
La descripción del diseño así como la terminología subyacente la vamos a introducir mediante el siguiente supuesto práctico.
Supuesto práctico 3
Abeto blanco, Abeto del Pirineo, es un árbol de gran belleza por la elegancia de sus formas y el exquisito perfume balsámico que destilan sus hojas y cortezas. Destilando hojas y madera se obtiene aceite de trementina muy utilizado en medicina contra torceduras y contusiones. En estos últimos años se ha observado que la producción de semillas ha descendido y con objeto de conseguir buenas producciones se proponen tres tratamientos. Se observa que árboles diferentes tienen distintas características naturales de reproducción, este efecto de las diferencias entre los árboles se debe de controlar y este control se realiza mediante bloques. En el experimento se utilizan 10 abetos, dentro de cada abeto se seleccionan tres ramas semejantes. Cada rama recibe exactamente uno de los tres tratamientos que son asignados aleatoriamente. Constituyendo cada árbol un bloque completo. Los datos obtenidos se presentan en la siguiente tabla donde se muestra el número de semillas producidas por rama.
 Figura 8: Tabla de datos del Supuesto Práctico 3.txt
Figura 8: Tabla de datos del Supuesto Práctico 3.txt
- Son diez Abetos en los que se aplican cuatro tratamientos distintos
- No hay ningún otro factor que pueda afectar de forma significativa a los resultados
- Los tratamientos se asignan en orden aleatorio a cada abeto
- El número de semillas observadas se muestra en la Figura 8.
- El experimentador forma bloques de manera que las unidades experimentales de cada bloque sean lo más homogéneas posible
- Los bloques entre sí han de ser heterogéneos
- Variable o factor bloque: Variable cuyo efecto sobre la variable respuesta no es directamente de interés, pero que se introduce en el experimento para obtener comparaciones homogéneas.
- Se reduce la variabilidad residual
Distinguimos dos tipos de diseños en bloques aleatorizados:
- Los diseños en bloques completos aleatorizados (Todos los tratamientos se prueban en cada bloque exactamente vez).
- Los diseños por bloques incompletos aleatorizados (Todos los tratamientos no están representados en cada bloque, y aquellos que sí están en uno en particular se ensayan en él una sola vez).
En este caso se trata de un diseño en bloques completos aleatorizados. El objetivo del estudio es comparar los tres tratamientos, por lo que se trata de un factor con tres niveles. Sin embargo, al realizar la medición sobre los distintos abetos, es posible que estos influyan sobre el número se semillas observadas. Por ello, y al no ser directamente motivo de estudio, los abetos es un factor secundario que recibe el nombre de bloque.
Nos interesa saber si los distintos tratamientos influyen en la producción de semillas, para ello realizamos el siguiente contraste de hipótesis:
![]() Expresión 11: Contraste de Hipótesis para los Tratamientos
Expresión 11: Contraste de Hipótesis para los Tratamientos
Es decir, contrastamos que no hay diferencia en las medias de los tres tratamientos frente a la alternativa de que al menos una media difiere de otra.
Pero, previamente hay que comprobar si la presencia del factor bloque (los abetos) está justificada. Para ello, realizamos el siguiente contraste de hipótesis:
![]() Expresión 12: Contraste de Hipótesis para los Bloques
Expresión 12: Contraste de Hipótesis para los Bloques
Es decir, contrastamos que no hay diferencia en las medias de los diez bloques frente a la alternativa de que al menos una media difiere de otra.
Este experimento se modeliza mediante un diseño en bloques completos al azar. El modelo matemático es:
![]() Expresión 13: Ecuación del diseño en bloques completos al azar
Expresión 13: Ecuación del diseño en bloques completos al azar
La fórmula expresa simbólicamente la idea de que cada observación yij (Número de semillas medida con el tratamiento i, del abeto j ), puede subdividirse en cuatro componentes: un efecto medio global μ, un efecto tratamiento τi (efecto del factor principal sobre el número de semillas), un efecto bloque βj (efecto del factor secundario (abetos) sobre el número de semillas) y una desviación aleatoria debida a causas desconocidas uij (Perturbaciones o error experimental). Este modelo tiene que verificar los siguientes supuestos:
-
Las 30 observaciones constituyen muestras aleatorias independientes, cada una de tamaño 3, de 30 poblaciones con medias μij, i=1, 2,…, 3 y j = 1, 2, .., 10.
-
Cada una de las 30 poblaciones es normal.
-
Cada una de las 30 poblaciones tiene la misma varianza.
-
Los efectos de los bloques y tratamientos son aditivos; es decir, no existe interacción entre los bloques y tratamientos. Esto significa que si hay diferencias entre dos tratamientos cualesquiera, estas se mantienen en todos los bloques (abetos).
Los tres primeros supuestos coinciden con los supuestos del modelo unifactorial, con la diferencia de que en el modelo unifactorial se examinaban I poblaciones y en este modelo se examinan IJ. El cuarto supuesto es característico del diseño en bloques. La no interacción entre los bloques y los tratamientos significa que los tratamientos tienen un comportamiento consistente a través de los bloques y que los bloques tienen un comportamiento consistente a través de los tratamientos. Expresado matemáticamente significa que la diferencia de los valores medios para dos tratamientos cualesquiera es la misma en todo un bloque y que la diferencia de los valores medios para dos bloques cualesquiera es la misma para cada tratamiento.
- Variable respuesta: Número de semillas
- Factor: Tratamiento que tiene tres niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Bloque: Abeto que tiene diez niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Modelo completo: Los tres tratamientos se prueban en cada bloque exactamente una vez.
- Tamaño del experimento: Número total de observaciones (30).
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto:
Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en la imagen, es decir, las observaciones en una sola columna y a continuación especificado su tratamiento y su bloque correspondiente.
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
> setwd(“F:/Desktop/Datos”)
> semillas<-read.table(“supuesto3.txt”, header = TRUE)
> semillas
y Tratamiento Abeto
1 7 1 1
2 9 2 1
3 10 3 1
4 8 1 2
5 9 2 2
6 10 3 2
7 9 1 3
8 9 2 3
9 12 3 3
10 10 1 4
11 9 2 4
12 12 3 4
A continuación debemos transformar tanto la columna de los tratamientos como la de los bloques en un factor para podemos realizar los cálculos posteriores adecuadamente.
> semillas$Tratamiento = factor(semillas$Tratamiento)
> semillas$Tratamiento
[1] 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3
Levels: 1 2 3
> semillas$Abeto = factor(semillas$Abeto)
> semillas$Abeto
[1] 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 8 8 8 9
[26] 9 9 10 10 10
Levels: 1 2 3 4 5 6 7 8 9 10
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
> mod = aov(y ~ Tratamiento + Abeto, data = semillas)
donde:
- y es el nombre de la columna de las observaciones
- Tratamiento es el nombre de la columna en la que están representados los tratamientos
- Abeto es el nombre de la columna en la que están representados los bloques
- data = data.frame en el que están guardados los datos
> mod
Call:
aov(formula = y ~ Tratamiento + Abeto, data = semillas)
Terms:
Tratamiento Abeto Residuals
Sum of Squares 16.2 54.8 15.8
Deg. of Freedom 2 9 18
Residual standard error: 0.936898
Estimated effects may be unbalanced
y a continuación mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
> summary(mod) # TABLA ANOVA
Df Sum Sq Mean Sq F value Pr(>F)
Tratamiento 2 16.2 8.100 9.228 0.00174 **
Abeto 9 54.8 6.089 6.937 0.00026 ***
Residuals 18 15.8 0.878
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Puesto que la construcción de bloques se ha diseñado para comprobar el efecto de una variable, nos preguntamos si ha sido eficaz su construcción. En caso afirmativo, la suma de cuadrados de bloques explicaría una parte sustancial de la suma total de cuadrados. También se reduce la suma de cuadrados del error dando lugar a un aumento del valor del estadístico de contraste experimental utilizado para contrastar la igualdad de medias de los tratamientos y posibilitando que se rechace la Hipótesis nula, mejorándose la potencia del contraste.
La construcción de bloques puede ayudar cuando se comprueba su eficacia pero debe evitarse su construcción indiscriminada. Ya que, la inclusión de bloques en un diseño da lugar a una disminución del número de grados de libertad para el error, aumenta el punto crítico para contrastar la Hipótesis nula y es más difícil rechazarla. La potencia del contraste es menor.
La Tabla ANOVA, muestra que:
-
El valor del estadístico de contraste de igualdad de bloques, F = 6.937 deja a su derecha un p-valor menor que 0.001, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de bloques. La eficacia de este diseño depende de los efectos de los bloques. Un valor grande de F de los bloques (6.937) implica que el factor bloque tiene un efecto grande. En este caso el diseño es más eficaz que el diseño completamente aleatorizado ya que si el cuadrado medio entre bloques es grande (6.089), el término residual será mucho menor (0.878) y el contraste principal de las medias de los tratamientos será más sensible a las diferencias entre tratamientos. Por lo tanto la inclusión del factor bloque en el modelo es acertada. Así, la producción de semillas depende del abeto.
Si los efectos de los bloques son muy pequeños, el análisis de bloque quizás no sea necesario y en caso extremo, cuando el valor de F de los bloques es próximo a 1, puede llegar a ser perjudicial, ya que el número de grados de libertad, (I-1)(J-1 ), del denominador de la comparación de tratamientos es menor que el número de grados de libertad correspondiente, IJ-I, en el diseño completamente aleatorizado. Pero, ¿Cómo saber cuándo se puede prescindir de los bloques? La respuesta la tenemos en el valor de la F experimental de los bloques, se ha comprobado que si dicho valor es mayor que 3, no conviene prescindir de los bloques para efectuar los contrastes.
-
El valor del estadístico de contraste de igualdad de tratamiento, F = 9.228 deja a su derecha un p-valor de 0.002, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de tratamientos. Así, los tratamientos influyen en el número de semillas. Es decir, existen diferencias significativas en el número de semillas entre los tres tratamientos.
El modelo que hemos propuesto hay que validarlo, para ello hay que comprobar si se verifican los cuatros supuestos expresados anteriormente.
Estudio de la Idoneidad del modelo
Como hemos dicho anteriormente, validar el modelo propuesto consiste en estudiar si las hipótesis básicas del modelo están o no en contradicción con los datos observados. Es decir si se satisfacen los supuestos del modelo: Normalidad, Independencia, Homocedasticidad. Para ello utilizamos procedimientos gráficos y analíticos.
En este modelo se ha supuesto otra hipótesis adicional:
Aditividad de los efectos de tratamiento y bloque (no existe interacción entre tratamiento y bloque). Por lo que hay que contrastar la hipótesis de aditividad de los efectos de tratamiento y bloque.
Hipótesis de aditividad entre los bloques y tratamientos
La interacción entre el factor bloque y los tratamientos vamos a estudiarla analíticamente mediante el Test de Interacción de un grado de Tukey
Para realizar este test en R tenemos que utilizar la library “daewr” y dentro de ella la función “Tukey1df”. De la siguiente forma:
Primero hay que instalar el paquete daewr
Para ello, seleccionar Paquetes/Instalar paquetes y de la lista escoger daewr. O bien utilizar la siguiente orden
> utils:::menuInstallPkgs()
Para realizar este contraste hay que utilizar la libray daewr, para ello realizamos la siguiente orden
> library(daewr)
> Tukey1df(semillas)
Source df SS MS F Pr>F
A 2 16.2 8.1
B 9 54.8 6.0889
Error 18 15.8 71.1
NonAdditivity 1 5475.752 5475.752 -17.05 1
Residual 17 -5459.952 -321.1736
Puesto que el p-valor (Pr > F) es 1 no rechazamos la hipótesis nula de no interacción, es decir, no hay interacción entre los tratamientos aplicados y los abetos.
Hipótesis de Normalidad
La normalidad las vamos a comprobar analíticamente y gráficamente.
Analíticamente mediante el contraste de Shapiro-Wilk que es adecuado cuando las muestras son pequeñas (n<50)
> shapiro.test(mod$residuals)
Shapiro-Wilk normality test
data: mod$residuals
W = 0.96415, p-value = 0.3935
Como podemos observar tenemos un p-valor de 0.3935 que aceptaría la hipótesis de normalidad por ser mayor al 5% (nivel de significación usual).
Gráficamente mediante el gráfico probabilístico normal. Para ello utilizamos la orden “qqnorm”
> qqnorm(mod$residuals)
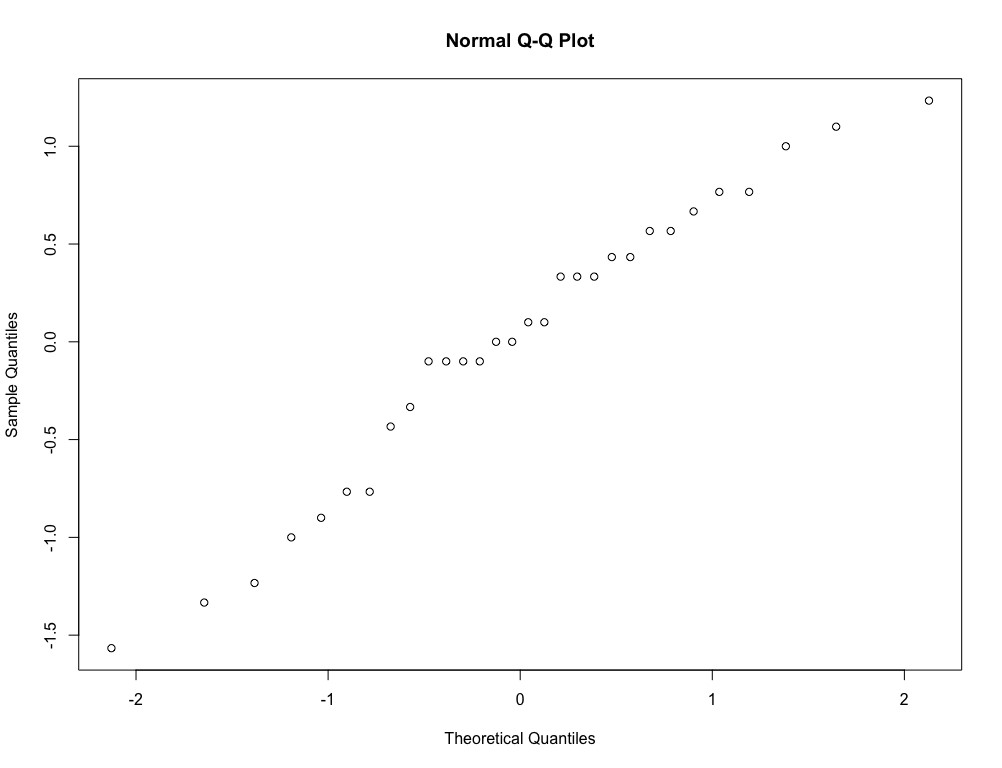
Figura 6: Estudio gráfico de la hipótesis de normalidad mediante el gráfico Q-Q Plot
En esta gráfica observamos que prácticamente todos los puntos se encuentran sobre la diagonal por lo tanto podemos decir que no muestra una desviación marcada de la normalidad.
Hipótesis de Homogeneidad de Varianzas
Para comprobar la hipótesis de homocedasticidad utilizamos el Test de Barlett distinguiendo entre la igualdad entre varianzas del factor principal y la igualdad de varianzas del factor bloque.
En nuestro ejemplo, el test para igualdad de varianzas del factor principal sería:
> bartlett.test(semillas$y, semillas$Tratamiento)
Bartlett test of homogeneity of variances
data: semillas$y and semillas$Tratamiento
Bartlett’s K-squared = 4.1729, df = 2, p-value = 0.1241
El p-valor es del 0.1241 que al ser mayor del nivel significación usual del 5% no podemos rechazar la hipótesis de igualdad de varianzas en el factor principal.
De la misma manera procedemos para el factor bloque:
> bartlett.test(semillas$y, semillas$Abeto)
Bartlett test of homogeneity of variances
data: semillas$y and semillas$Abeto
Bartlett’s K-squared = 4.0723, df = 9, p-value = 0.9066
El p-valor es mayor que 0.05 por lo que no podemos rechazar la hipótesis de igualdad de varianzas en el factor bloque.
Hipótesis de Independencia
Comprobaremos si se satisface el supuesto de independencia entre los residuos. Para ello tenemos que representar un gráfico de los residuos tipificados frente a los pronosticados. En R obtenemos varios gráficos a la vez que están incluidos en la estimación del modelo.
Para verlos de forma correcta hacemos uso de las siguientes órdenes:
> layout(matrix(c(1,2,3,4),2,2))
> plot(mod)
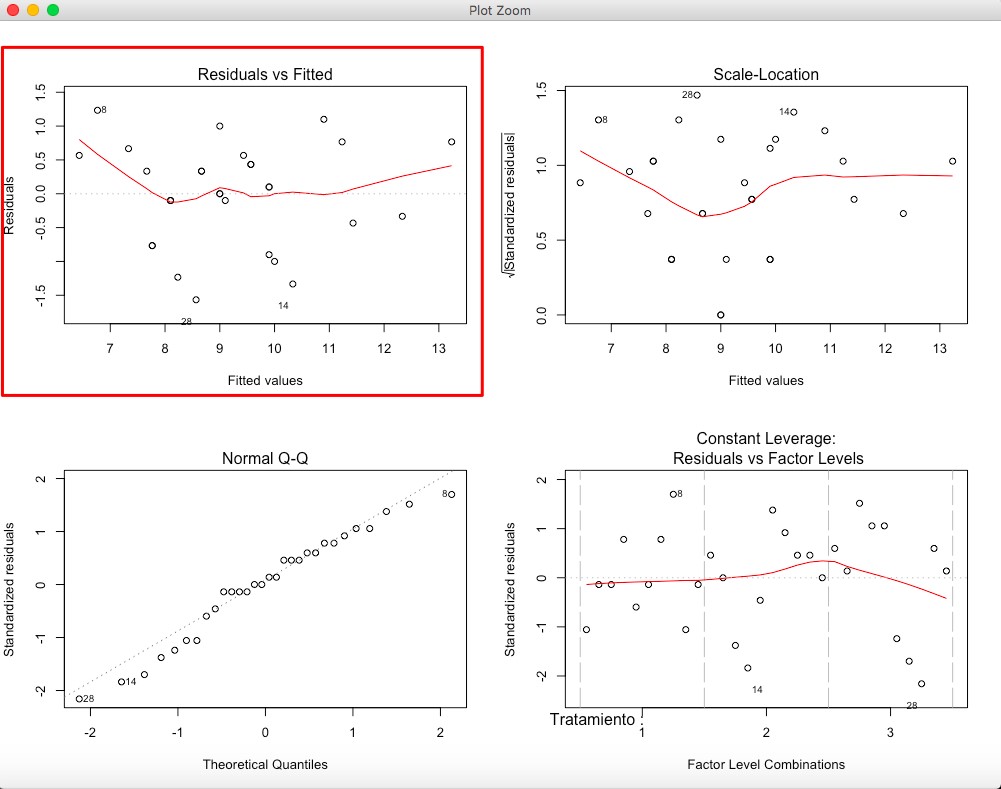
Figura 7: Estudio gráfico de la hipótesis de independencia de los residuos
Nos fijamos en el primer gráfico que representa los residuos frente a los valores ajustados y observamos que no hay ninguna tendencia sistemática. Concluimos que no hay sospechas para que se incumpla la hipótesis de independencia.
Comparaciones múltiples
Hemos probado anteriormente que se rechaza la Hipótesis nula de igualdad de tratamientos. Así, los tratamientos influyen en el número de semillas. Es decir, existen diferencias significativas en el número de semillas entre los tres tratamientos. Para saber entre que parejas de días estas diferencias son significativas aplicamos una prueba Post-hoc.
El contraste de Comparaciones múltiples que vamos a utilizar es el Test de Duncan. Para poder hacer uso de él en R tenemos que instalar en primer lugar el paquete “agricolae” y dentro de él la función “duncan.test”.
Destacar que este test hace las comparaciones especificándole si es para el factor principal o el factor bloque.
Comenzamos con el factor principal:
> (duncan=duncan.test(mod, “Tratamiento” , group = T))
$`statistics`
MSerror Df Mean CV
0.8777778 18 9.2 10.18367
$parameters
test name.t ntr alpha
Duncan Tratamiento 3 0.05
$duncan
Table CriticalRange
2 2.971152 0.8802727
3 3.117384 0.9235973
$means
y std r Min Max Q25 Q50 Q75
1 8.3 1.337494 10 7 11 7.25 8 8.75
2 9.2 1.135292 10 8 12 9.00 9 9.00
3 10.1 2.183270 10 7 14 9.25 10 11.50
$comparison
NULL
$groups
y groups
3 10.1 a
2 9.2 b
1 8.3 c
attr(,”class”)
[1] “group”
En el apartado “$groups” concluimos que los tres tratamientos difieren significativamente entre sí.
Se observa que la concentración media del número de semillas es mayor con el Tratamiento3 (10.1) y menor con el Tratamiento1 (8.3).
Para el factor bloque:
> (duncan=duncan.test(mod, “Abeto” , group = T))
$`statistics`
MSerror Df Mean CV
0.8777778 18 9.2 10.18367
$parameters
test name.t ntr alpha
Duncan Abeto 10 0.05
$duncan
Table CriticalRange
2 2.971152 1.607151
3 3.117384 1.686250
4 3.209655 1.736161
5 3.273593 1.770746
6 3.320327 1.796026
7 3.355651 1.815133
8 3.382941 1.829895
9 3.404326 1.841462
10 3.421226 1.850604
$means
y std r Min Max Q25 Q50 Q75
1 8.666667 1.5275252 3 7 10 8.0 9 9.5
10 9.000000 1.0000000 3 8 10 8.5 9 9.5
2 9.000000 1.0000000 3 8 10 8.5 9 9.5
3 10.000000 1.7320508 3 9 12 9.0 9 10.5
4 10.333333 1.5275252 3 9 12 9.5 10 11.0
5 12.333333 1.5275252 3 11 14 11.5 12 13.0
6 9.000000 1.0000000 3 8 10 8.5 9 9.5
7 7.333333 0.5773503 3 7 8 7.0 7 7.5
8 7.666667 0.5773503 3 7 8 7.5 8 8.0
9 8.666667 1.5275252 3 7 10 8.0 9 9.5
$comparison
NULL
$groups
y groups
5 12.333333 a
4 10.333333 b
3 10.000000 b
10 9.000000 bc
2 9.000000 bc
6 9.000000 bc
1 8.666667 bc
9 8.666667 bc
8 7.666667 c
7 7.333333 c
attr(,”class”)
[1] “group”
Se observa que la prueba de Duncan ha agrupado los abetos 7, 8, 1, 9, 2, 6 y 10 en un mismo grupo, 1, 9 ,2 6, 10, 3 y 4, en otro grupo y un tercer está formada únicamente por el Abeto5. Inmediatamente se ve que por ejemplo el Abeto5 difiere de todos los demás, siendo en este abeto donde se produce el mayor número de semillas (12.333) y el menor en el Abeto7 (7.333).
Diseño en bloques Incompletos Aleatorizados
En los diseños en bloques Aleatorizados, puede suceder que no sea posible realizar todos los tratamientos en cada bloque. En estos casos es posible usar diseños en bloques Aleatorizados en los que cada tratamiento no está presente en cada bloque. Estos diseños reciben el nombre de diseño en bloque incompleto aleatorizado siendo uno de los más utilizados el diseño en bloque incompleto balanceado (BIB)
El diseño de bloques incompletos balanceado (BIB) compara todos los tratamientos con igual precisión.
Este diseño experimental debe verificar:
-
Cada tratamiento ocurre el mismo número de veces en el diseño.
-
Cada par de tratamientos ocurren juntos el mismo número de veces que cualquier otro par.
Supongamos que se tienen \( I \) tratamientos de los cuales sólo pueden experimentar \( K \) tratamientos en cada bloque \( (K < I) \). Los parámetros que caracterizan este modelo son:
-
\( I \), \( J \) y \( K \) son el número de tratamientos, el número de bloques y el número de tratamientos por bloque, respectivamente.
-
\( R \), número de veces que cada tratamiento se presenta en el diseño, es decir el número de réplicas de un tratamiento dado.
-
\( \lambda \), número de bloques en los que un par de tratamientos ocurren juntos.
-
\( N \), número de observaciones.
Estos parámetros deben verificar las siguientes relaciones:
\( \lambda = R \displaystyle \frac {K-1}{I-1} = \)
Expresión 14: Relación en Bloques Incompletos
donde \( J \geq I \) y \( N = IR = JK \)
- Si \( J = I \) el diseño recibe el nombre de simétrico.
Al igual que en el diseño en bloques completo, la asignación de los tratamientos a las unidades experimentales en cada bloque se debe realizar en forma aleatoria.
Este diseño lo estudiaremos a continuación mediante el supuesto práctico 4
Supuesto práctico 4
Se realiza un estudio para comprobar la efectividad en el retraso del crecimiento de bacterias utilizando cuatro soluciones diferentes para lavar los envases de la leche. El análisis se realiza en el laboratorio y sólo se pueden realizar seis pruebas en un mismo día. Como los días son una fuente de variabilidad potencial, el investigador decide utilizar un diseño aleatorizado por bloques, pero al recopilar las observaciones durante seis días no ha sido posible aplicar todos los tratamientos en cada día, sino que sólo se han podido aplicar dos de las cuatro soluciones cada día. Se decide utilizar un diseño en bloques incompletos balanceado, donde I = 4 y K = 2.
Un posible diseño para estos parámetros lo proporciona la tabla correspondiente al Diseño 5 del Fichero-Adjunto, con R = 3, J = 6 y λ = 1. La disposición del diseño y las observaciones obtenidas se muestran en la siguiente tabla.
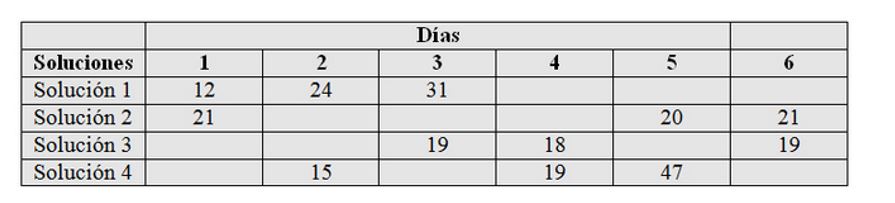 Figura 8: Tabla de datos del Supuesto Práctico 4.txt
Figura 8: Tabla de datos del Supuesto Práctico 4.txt
En el ejemplo:
- N = I R = J K. En efecto, ya que N= 12; I = 4, J = 6; R = 3 y K = 2.
-
λ = 3 × 1⁄3 = 1
El objetivo principal es estudiar la efectividad en el retraso del crecimiento de bacterias utilizando cuatro soluciones, por lo que se trata de un factor con cuatro niveles. Sin embrago, como los días son una fuente de variabilidad potencial, consideramos un factor bloque con seis niveles.
- Variable respuesta: Número de bacterias
- Factor: Soluciones que tiene cuatro niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Bloque: Días que tiene seis niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Modelo incompleto: Todos los tratamientos no se prueban en cada bloque.
- Tamaño del experimento: Número total de observaciones (12).
Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
> bacterias = read.table(“bacterias.txt”, header = TRUE)
> bacterias
y Soluciones Días
1 12 1 1
2 24 1 2
3 31 1 3
4 21 2 1
5 20 2 5
6 21 2 6
7 19 3 3
8 18 3 4
9 19 3 6
10 15 4 2
11 19 4 4
12 47 4 5
A continuación debemos transformar tanto la columna de los tratamientos como la de los bloques en un factor para poder realizar los cálculos posteriores adecuadamente.
> bacterias$Soluciones = factor( bacterias$Soluciones)
> bacterias$Dias = factor( bacterias$Días)
Para poder analizar los datos mediante un diseño BIB debemos instalar y cargar dos paquetes de R especializados en este tipo de diseños:
> library(daewr)
> library(AlgDesign)
La función “BIBsize(t , k)” de la librería daewr nos permite saber si el diseño puede realizarse. Calcula los parámetros del diseño donde
- t = número de niveles del factor tratamiento.
- k = número de tratamientos por bloque.
Ejecutamos:
> BIBsize(t = 4 , k = 2)
Posible BIB design with b= 6 and r= 3 lambda= 1
El análisis de este modelo lo podemos realizar en R de dos formas:
-
Realizaremos el análisis evaluando primero el efecto de los tratamientos y después el de los bloques utilizando dos funciones
- Para evaluar el efecto de los tratamientos, la suma de cuadrados de tratamientos debe ajustarse por bloques, por lo tanto primero se introducen los bloques y después los tratamientos.
- Para calcular la tabla ANOVA hacemos uso de la función “aov” (aov(y ~ A + B, data=mydataframe) asume suma de cuadrados tipo I) de la siguiente forma:
> mod1 <- aov(y ~ Dias + Soluciones, data = bacterias )
donde:
- y = nombre de la columna de las observaciones
- Soluciones = nombre de la columna en la que están representados los tratamientos
- Dias = nombre de la columna en la que están representados los bloques
- data = data.frame en el que están guardados los datos
> mod1
Call:
aov(formula = y ~ Dias + Soluciones, data = bacterias)
Terms:
Dias Soluciones Residuals
Sum of Squares 387.6667 123.2500 396.7500
Deg. of Freedom 5 3 3
Residual standard error: 11.5
Estimated effects may be unbalanced
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA)
> summary(mod1)
Df Sum Sq Mean Sq F value Pr(>F)
Dias 5 387.7 77.53 0.586 0.720
Soluciones 3 123.3 41.08 0.311 0.819
Residuals 3 396.7 132.25
El valor del estadístico de contraste de igualdad de Soluciones, F = 0.311, deja a su derecha un p-valor 0.819, mayor que el nivel de significación del 5%, por lo que no se rechaza la Hipótesis Nula de igualdad de tratamientos. Por lo tanto el tipo de solución para lavar los envases de la leche no influye en el retraso del crecimiento de bacterias.
- Para evaluar el efecto de los bloques, la suma de cuadrados de bloques debe ajustarse por los tratamientos, por lo tanto primero se introducen los tratamientos y después los bloques:
> mod2 <- aov(y ~ Soluciones + Dias, data = bacterias )
> mod2
Call:
aov(formula = y ~ Soluciones + Dias, data = bacterias)
Terms:
Soluciones Dias Residuals
Sum of Squares 113.6667 397.2500 396.7500
Deg. of Freedom 3 5 3
Residual standard error: 11.5
Estimated effects may be unbalanced
> summary(mod2)
Df Sum Sq Mean Sq F value Pr(>F)
Soluciones 3 113.7 37.89 0.286 0.834
Dias 5 397.2 79.45 0.601 0.712
Residuals 3 396.7 132.25
El valor del estadístico de contraste de igualdad de Días, F = 0.601, deja a su derecha un p-valor 0.712, mayor que el nivel de significación del 5%, por lo que no se rechaza la Hipótesis nula de igualdad de bloques. Por lo tanto los días en los que se realiza la prueba para lavar los envases de la leche no influyen en el retraso del crecimiento de bacterias.
Con este ejemplo se ilustra el hecho de decidir si se prescinde o no de los bloques. Hay situaciones en las que, aunque los bloques no resulten significativamente diferentes no es conveniente prescindir de ellos. Pero ¿cómo saber cuándo se puede prescindir de los bloques? La respuesta la tenemos en el valor de la F de los bloques, experimentalmente se ha comprobado que si dicho valor es mayor que 3, no conviene prescindir de los bloque para efectuar los contrastes.
En esta situación si se puede prescindir del efecto de los bloques y estudiar el modelo unifactorial correspondiente, cuyo único factor es: Soluciones.
2. Realizaremos el análisis evaluando tanto para los tratamientos como para los bloques ejecutando solo una función.
Para ello necesitamos instalar y cargar el paquete “car”:
IMPORTANTE: Hemos comprobado que utilizando la versión del paquete “car” 3.0-0, encontramos un error y no permite su utilización, por lo que descargamos una versión anterior, concretamente car_2.1-6.tar.gz. Pinchamos en este enlace y guardamos el archivo en el escritorio
Recordad que para la utilización de un paquete es necesario instalarlo y cargarlo. Para ello:
- Accedemos a Paquetes/Install package(s) from local file y elegimos el paquete descargado.
- Posteriormente lo cargamos con Paquetes/Cargar paquetes
Nota: Para instalar un paquete directamente de R, procederemos de la forma siguiente
- Accedemos a la página https://cran.r-project.org/index.html.
- Seleccionamos Packages
- Seleccionamos Table of available packages, sorted by name
- Seleccionamos paquete car
- Seleccionamos Old sources car archive
- Seleccionamos el paquete car_2.1-6.tar.gz y lo guardamos en el escritorio.
Una vez instalado cargado el paquete realizamos el ANOVA
> mod3 <- lm(y ~ Soluciones + Dias, data = bacterias )
> mod3
Call:
lm(formula = y ~ Soluciones + Dias, data = bacterias)
Coefficients:
(Intercept) Soluciones2 Soluciones3 Soluciones4 Dias2 Dias3
20.000 -7.000 -6.750 1.750 -1.375 8.375
Dias4 Dias5 Dias6
1.000 16.125 6.875
> car::Anova(mod3, type=”III”)
Anova Table (Type III tests)
Response: y
Sum Sq Df F value Pr(>F)
(Intercept) 533.33 1 4.0328 0.1382
Soluciones 123.25 3 0.3106 0.8187
Dias 397.25 5 0.6008 0.7118
Residuals 396.75 3
Los resultados obtenidos coinciden con los realizados primero a los tratamientos y después a los bloques.
Diseño en Cuadrados Latinos
Hemos estudiado en el apartado anterior que los diseños en bloques completos aleatorizados utilizan un factor de control o variable de bloque con objeto de eliminar su influencia en la variable respuesta y así reducir el error experimental. Los diseños en cuadrados latinos utilizan dos variables de bloque para reducir el error experimental.
Un inconveniente que presentan a veces los diseños es el de requerir excesivas unidades experimentales para su realización. Un diseño en bloques completos con un factor principal y dos factores de bloque, con \( K1 \), \( K2 \) y \( K3 \) niveles en cada uno de los factores, requiere \( K1 \times K2 \times K3 \) unidades experimentales. En un experimento puede haber diferentes causas, por ejemplo de índole económico, que no permitan emplear demasiadas unidades experimentales, ante esta situación se puede recurrir a un tipo especial de diseños en bloques incompletos aleatorizados. La idea básica de estos diseños es la de fracción es decir, seleccionar una parte del diseño completo de forma que, bajo ciertas hipótesis generales, permita estimar los efectos que interesan.
Uno de los diseños en bloques incompletos aleatorizados más importante con dos factores de control es el modelo en cuadrado latino, dicho modelo requiere el mismo número de niveles para los tres factores.
En general, para \( K \) niveles en cada uno de los factores, el diseño completo en bloques aleatorizados utiliza \( K^2 \) bloques, aplicándose en cada bloque los \( K \) niveles del factor principal, resultando un total de \( K^3 \) unidades experimentales.
Los diseños en cuadrado latino reducen el número de unidades experimentales a \( K^2 \) utilizando los \( K^2 \) bloques del experimento, pero aplicando sólo un tratamiento en cada bloque con una disposición especial. De esta forma, si \( K \) fuese 4, el diseño en bloques completos necesitaría \( 4^3 = 64 \) observaciones, mientras que el diseño en cuadrado latino sólo necesitaría \( 4^2 = 16 \) observaciones.
Los diseños en cuadrados latinos son apropiados cuando es necesario controlar dos fuentes de variabilidad. En dichos diseños el número de niveles del factor principal tiene que coincidir con el número de niveles de las dos variables de bloque o factores secundarios y además hay que suponer que no existe interacción entre ninguna pareja de factores.
Recibe el nombre de cuadrado latino de orden \( K \) a una disposición en filas y columnas de \( K \) letras latinas, de tal forma que cada letra aparece una sola vez en cada fila y en cada columna.
En resumen, podemos decir que un diseño en cuadrado latino tiene las siguientes características:
-
Se controlan tres fuentes de variabilidad, un factor principal y dos factores de bloque.
-
Cada uno de los factores tiene el mismo número de niveles, \( K \).
-
Cada nivel del factor principal aparece una vez en cada fila y una vez en cada columna.
-
No hay interacción entre los factores.
En el Fichero-Adjunto se muestran algunos cuadrados latinos estándares para los órdenes 3, 4, 5, 6, 7, 8 y 9.
Este diseño lo estudiaremos a continuación mediante el supuesto práctico 5
Supuesto práctico 5
Se estudia el rendimiento de un proceso químico en seis tiempos de reposo, A, B, C, D, E y F. Para ello, se consideran seis lotes de materia prima que reaccionan con seis concentraciones de ácido distintas, de manera que cada lote de materia prima en cada concentración de ácido se somete a un tiempo de reposo. Tanto la asignación de los tiempos de reposo a los lotes de materia prima, como la concentración de ácido, se hizo de forma aleatoria. Los datos del rendimiento del proceso químico se muestran en la siguiente tabla.
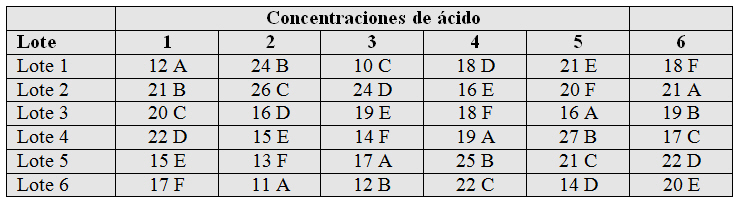 Figura 9: Tabla de datos del Supuesto Práctico 5.doc
Figura 9: Tabla de datos del Supuesto Práctico 5.doc
El objetivo principal es estudiar la influencia de seis tiempos de reposo en el rendimiento de un proceso químico, por lo que se trata de un factor con seis niveles. Sin embargo, como los lotes de materia prima y las concentraciones son dos fuentes de variabilidad potencial, consideramos dos factores de bloque con seis niveles cada uno.
- Variable respuesta: Rendimiento
- Factor: Tiempo de reposo que tiene seis niveles. Es un factor de efectos fijos ya que viene decidido que niveles concretos se van a utilizar.
- Bloques: Lotes y Concentraciones, ambos con seis niveles y ambos son factores de efectos fijos.
- Tamaño del experimento: Número total de observaciones (36).
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto:
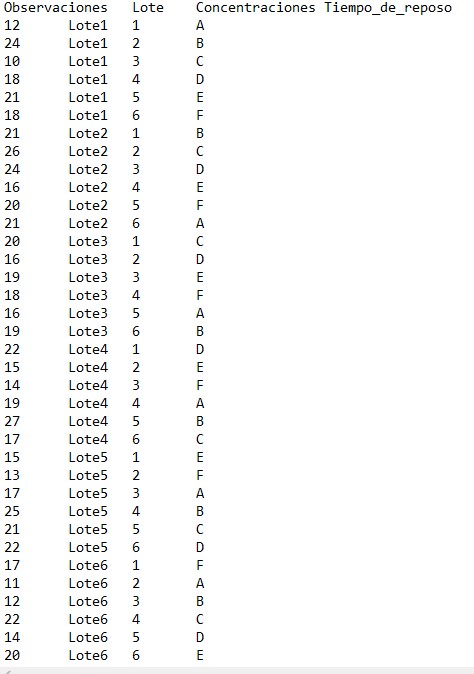
Figura 10: Tabla de datos del Supuesto Práctico 5.txt
Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en la imagen, es decir, las observaciones en una sola columna y a continuación especificado su tratamiento, su bloque y después la letra latina correspondiente.
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
> latino <- read.table(“Lotes2.txt”, header = TRUE, dec= “,”)
> latino
Observaciones Lote Concentraciones Tiempo_de_reposo
1 12 Lote1 1 A
2 24 Lote1 2 B
3 10 Lote1 3 C
4 18 Lote1 4 D
5 21 Lote1 5 E
6 18 Lote1 6 F
7 21 Lote2 1 B
8 26 Lote2 2 C
9 24 Lote2 3 D
10 16 Lote2 4 E
11 20 Lote2 5 F
12 21 Lote2 6 A
13 20 Lote3 1 C
14 16 Lote3 2 D
15 19 Lote3 3 E
16 18 Lote3 4 F
17 16 Lote3 5 A
18 19 Lote3 6 B
19 22 Lote4 1 D
20 15 Lote4 2 E
21 14 Lote4 3 F
22 19 Lote4 4 A
23 27 Lote4 5 B
24 17 Lote4 6 C
25 15 Lote5 1 E
26 13 Lote5 2 F
27 17 Lote5 3 A
28 25 Lote5 4 B
29 21 Lote5 5 C
30 22 Lote5 6 D
31 17 Lote6 1 F
32 11 Lote6 2 A
33 12 Lote6 3 B
34 22 Lote6 4 C
35 14 Lote6 5 D
36 20 Lote6 6 E
A continuación debemos transformar tanto la columna de los tratamiento como la de los bloques en un factor para podemos realizar los cálculos posteriores adecuadamente.
> latino$Lote <- factor(latino$Lote)
> latino$Concentraciones <- factor(latino$Concentraciones)
> latino$Tiempo_de_reposo <- factor(latino$Tiempo_de_reposo)
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
> mod1 <- aov(Observaciones~ Lote + Concentraciones + Tiempo_de_reposo, data = latino )
donde:
- Observaciones: Nombre de la columna de las observaciones
- Lote : Nombre de la columna en la que están representados los tratamientos
- Concentraciones : Nombre de la columna en la que está representado el primer factor bloque
- Tiempo_de_reposo: Nombre de la columna en la que está representado el segundo factor bloque (letras latinas)
- data = data.frame en el que están guardados los datos
> mod1
Call:
aov(formula = Observaciones ~ Lote + Concentraciones + Tiempo_de_reposo,
data = latino)
Terms:
Lote Concentraciones Tiempo_de_reposo Residuals
Sum of Squares 99.5556 70.5556 117.8889 346.5556
Deg. of Freedom 5 5 5 20
Residual standard error: 4.162665
Estimated effects may be unbalanced
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
> summary(mod1)
Df Sum Sq Mean Sq F value Pr(>F)
Lote 5 99.6 19.91 1.149 0.368
Concentraciones 5 70.6 14.11 0.814 0.553
Tiempo_de_reposo 5 117.9 23.58 1.361 0.281
Residuals 20 346.6 17.33
Observando los valores de los p-valores, 0.281, 0.368 y 0.553; mayores respectivamente que el nivel de significación del 5%, deducimos que ningún efecto es significativo.
Diseño en Cuadrados Greco-Latinos
El modelo en cuadrado greco-latino se puede considerar como una extensión del modelo en cuadrado latino en el que se incluye una tercera variable control o variable de bloque. En este modelo como en el diseño en cuadrado latino, todos los factores deben tener el mismo número de niveles, \( K \), y el número de observaciones necesarias sigue siendo \( K^2 \). Este diseño es, por tanto, una fracción del diseño completo en bloques aleatorizados con un factor principal y tres factores secundarios que requeriría \( K^4 \) observaciones.
Los cuadrados greco-latinos se obtienen por superposición de dos cuadrados latinos del mismo orden y ortogonales entre sí, uno de los cuadrados con letras latinas el otro con letras griegas. Dos cuadrados reciben el nombre de ortogonales si, al superponerlos, cada letra latina y griega aparecen juntas una sola vez en el cuadrado resultante.
En el Fichero-Adjunto se muestra una tabla de cuadrados latinos que dan lugar, por superposición de dos de ellos, a cuadrados greco-latinos. Notamos que no es posible formar cuadrados greco-latinos de orden 6.
La Tabla siguiente ilustra un cuadrado greco-latino para \( K= 4 \),
\( \begin{array} {|c|c|c|c|} \hline A & B & C & D \\ \alpha & \beta & \gamma & \delta \\ \hline D & C & B & A \\ \gamma & \delta & \alpha & \beta \\ \hline B & A & D & C \\ \delta & \gamma & \beta & \alpha \\ \hline C & D & A & B \\ \beta & \alpha & \delta & \gamma \\ \hline \end{array} \)
Figura 11: Ejemplo de un cuadrado greco-latino para K=4
Este diseño lo estudiaremos a continuación mediante el supuesto práctico 6.
Supuesto práctico 6
Para comprobar el rendimiento de un proceso químico en cinco tiempos de reposo, se consideran cinco lotes de materia prima que reaccionan con cinco concentraciones de ácido distintas a cinco temperaturas distintas, de manera que cada lote de materia prima con cada concentración de ácido y cada temperatura se someten a un tiempo de reposo. Tanto la asignación de los tiempos de reposo a los lotes de materia prima, como las concentraciones de ácido, y las temperaturas, se hizo de forma aleatoria. En este estudio el científico considera que tanto los lotes de materia prima, las concentraciones y las temperaturas pueden influir en el rendimiento del proceso, por lo que los considera como variables de bloque cada una con cinco niveles y decide plantear un diseño por cuadrados greco-latinos como el que muestra en la siguiente tabla.
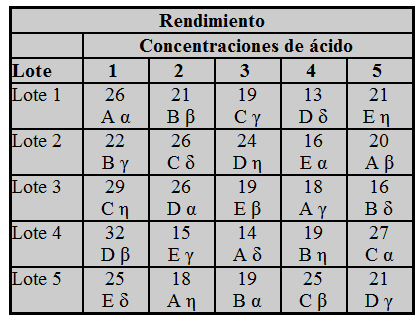 Figura 12: Tabla de datos del Supuesto Práctico 6.doc
Figura 12: Tabla de datos del Supuesto Práctico 6.doc
La variable respuesta que vamos a estudiar es el rendimiento del proceso químico. El factor principal es tiempo de reposo que se presenta con cinco niveles.
- Variable respuesta: Rendimiento
- Factor: Tiempos de reposo que tiene cinco niveles. Es un factor de efectos fijos ya que viene decidido que niveles concretos se van a utilizar.
- Bloques: Lotes, Concentraciones y Temperaturas, cada uno con cinco niveles y de efectos fijos.
- Tamaño del experimento: Número total de observaciones (25).
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto.
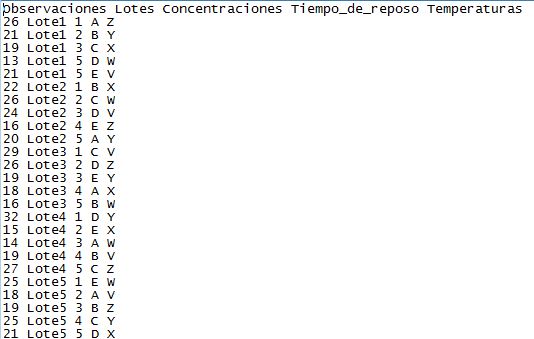
Figura 13: Tabla de datos del Supuesto Práctico 6.txt
Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en la imagen, es decir, las observaciones en una sola columna y a continuación especificado su tratamiento, su bloque correspondiente y después la letra latina y griega correspondiente (En este caso hemos cambiado las letras griegas como las últimas del alfabeto latino por facilidad a la hora de escribirlas).
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
> setwd(“C:/Users/Usuario/Desktop/Datos”)
> greco <- read.table(“Lotes2.txt”, header = TRUE, dec= “,”)
> greco
Observaciones Lotes Concentraciones Tiempo_de_reposo Temperaturas
1 26 Lote1 1 A Z
2 21 Lote1 2 B Y
3 19 Lote1 3 C X
4 13 Lote1 5 D W
5 21 Lote1 5 E V
6 22 Lote2 1 B X
7 26 Lote2 2 C W
8 24 Lote2 3 D V
9 16 Lote2 4 E Z
10 20 Lote2 5 A Y
11 29 Lote3 1 C V
12 26 Lote3 2 D Z
13 19 Lote3 3 E Y
14 18 Lote3 4 A X
15 16 Lote3 5 B W
16 32 Lote4 1 D Y
17 15 Lote4 2 E X
18 14 Lote4 3 A W
19 19 Lote4 4 B V
20 27 Lote4 5 C Z
21 25 Lote5 1 E W
22 18 Lote5 2 A V
23 19 Lote5 3 B Z
24 25 Lote5 4 C Y
25 21 Lote5 5 D X
A continuación debemos transformar tanto la columna de los tratamiento como la de los bloques en un factor para podemos realizar los cálculos posteriores adecuadamente.
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
> greco <- read.table(“Lotes2.txt”, header = TRUE, dec= “,”)
> greco$Lote <- factor(greco$Lote)
> greco$Temperaturas <- factor(greco$Temperaturas)
> greco$Tiempo_de_reposo <- factor(greco$Tiempo_de_reposo)
> greco$Concentraciones <- factor(greco$Concentraciones)
> mod1 <- aov(Observaciones~ Lote + Concentraciones + Tiempo_de_reposo + Temperaturas, data = greco )
> mod1
Call:
aov(formula = Observaciones ~ Lote + Concentraciones + Tiempo_de_reposo +
Temperaturas, data = greco)
Terms:
Lote Concentraciones Tiempo_de_reposo Temperaturas Residuals
Sum of Squares 9.76 226.16 156.16 94.96 83.52
Deg. of Freedom 4 4 4 4 8
Residual standard error: 3.231099
Estimated effects may be unbalanced
donde:
- Observaciones: Nombre de la columna de las observaciones
- Lote: Nombre de la columna en la que están representados los tratamientos
- Concentraciones = Nombre de la columna en la que está representado el primer factor bloque
- Tiempo_de_reposo = Nombre de la columna en la que está representado el segundo factor bloque (letras latinas)
- Temperaturas: Nombre de la columna en la que está representado el tercer factor bloque
- Data: data.frame en el que están guardados los datos
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
> summary(mod1)
Df Sum Sq Mean Sq F value Pr(>F)
Lote 4 9.76 2.44 0.234 0.9117
Concentraciones 4 226.16 56.54 5.416 0.0207 *
Tiempo_de_reposo 4 156.16 39.04 3.739 0.0532 .
Temperaturas 4 94.96 23.74 2.274 0.1500
Residuals 8 83.52 10.44
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Observando los valores de los p-valores, 0.150, 0.053, 0.912 y 0.020, deducimos que el único efecto significativo, al nivel de significación del 5%, es el efecto de las distintas concentraciones sobre el rendimiento del proceso químico.
Diseño en Cuadrados de Youden
Hemos estudiado que en el diseño en cuadrado latino se tiene que verificar que los tres factores tengan el mismo número de niveles, es decir que hay el mismo número de filas, de columnas y de letras latinas. Sin embargo, puede suceder que el número de niveles disponibles de uno de los factores de control sea menor que el número de tratamientos, en este caso estaríamos ante un diseño en cuadrado latino incompleto. Estos diseños fueron estudiados por W.J. Youden y se conocen con el nombre de cuadrados de Youden.
Este diseño lo estudiaremos a continuación mediante el supuesto práctico 7.
Supuesto práctico 7
Consideremos de nuevo el experimento sobre el rendimiento de un proceso químico en el que se está interesado en estudiar seis tiempos de reposo, A, B, C, D, E y F y se desea eliminar estadísticamente el efecto de los lotes materia prima y de las concentraciones de ácido distintas. Pero supongamos que sólo se dispone de cinco tipos de concentraciones. Para analizar este experimento se decidió utilizar un cuadrado de Youden con seis filas (los lotes de materia prima), cinco columnas (las distintas concentraciones) y seis letras latinas (los tiempos de reposo). Los datos correspondientes se muestran en la siguiente tabla.
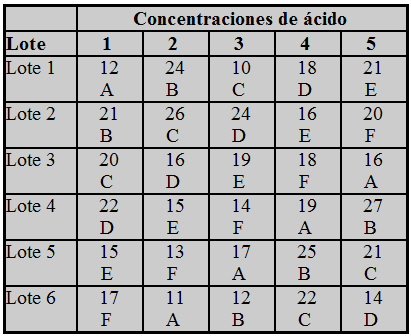 Figura 14: Tabla de datos del Supuesto Práctico 7.doc
Figura 14: Tabla de datos del Supuesto Práctico 7.doc
Observamos que este diseño se convierte en un cuadrado latino si se le añade la columna F, A, B, C, D y E. En general, un cuadrado de Youden podemos considerarlo como un cuadrado latino al que le falta al menos una columna. Sin embargo, un cuadrado latino no se convierte en un cuadrado de Youden eliminando arbitrariamente más de una columna.
Un cuadrado de Youden se puede considerar como un diseño en bloques incompletos balanceado y simétrico en el que las filas corresponden a los bloques. En efecto, si asignamos
-
el factor principal a las letras latinas,
-
un factor secundario, el que tiene el mismo número de niveles que el factor principal, a las filas,
-
un factor secundario, el que tiene menor número de niveles que el factor principal, a las columnas,
entonces, un cuadrado de Youden es un diseño en bloques incompletos balanceado y simétrico en el que
- Cada tratamiento ocurre una vez en cada columna.
- La posición del tratamiento dentro de un bloque indica el nivel del factor secundario correspondiente a las columnas.
- El número de réplicas de un tratamiento dado es igual al número de tratamientos por bloque.
Recordamos que los parámetros que caracterizan este modelo son:
-
I, J y K son el número de tratamientos, el número de bloques y el número de tratamientos por bloque, respectivamente.
-
R, número de veces que cada tratamiento se presenta en el diseño, es decir el número de réplicas de un tratamiento dado.
-
λ , número de bloques en los que un par de tratamientos ocurren juntos.
-
N, número de observaciones.
Los valores de los parámetros del modelo en este ejemplo son:
N = I R = J K. En efecto, ya que N= 30; I = 6 = J ; R = K = 5.
![]() Expresión 15: Relación en Bloques Incompletos
Expresión 15: Relación en Bloques Incompletos
El objetivo principal es estudiar la influencia de seis tiempos de reposo en el rendimiento de un proceso químico, por lo que se trata de un factor con seis niveles. Sin embargo, como los lotes de materia prima y las concentraciones son dos fuentes de variabilidad potencial, consideramos dos factores de bloque con seis y cinco niveles, respectivamente.
- Variable respuesta: Rendimiento
- Factor: Tiempo de reposo que tiene seis niveles. Es un factor de efectos fijos ya que viene decidido que niveles concretos se van a utilizar.
- Bloques: Lotes y Concentraciones, con seis y cinco niveles, respectivamente y ambos son factores de efectos fijos.
- Tamaño del experimento: Número total de observaciones (30).
-
Nombre: Rendimiento ; Tipo: Numérico ; Anchura: 2 ; Decimales: 0
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto:
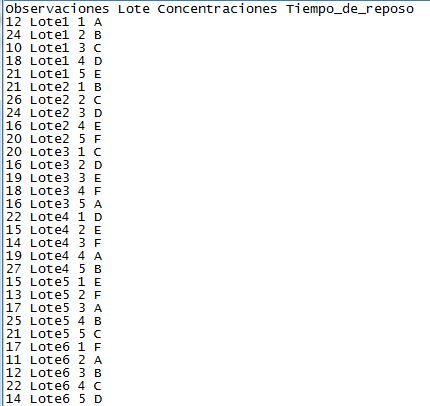
Figura 15: Tabla de datos del Supuesto Práctico 7.txt
Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en la imagen, es decir, las observaciones en una sola columna y a continuación especificado su tratamiento, su bloque correspondiente y después la letra latina correspondiente.
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
> setwd(“C:/Users/Usuario/Desktop/Datos”)
> youden <- read.table(“Lotes3.txt”, header = TRUE)
> youden
Observaciones Lote Concentraciones Tiempo_de_reposo
1 12 Lote1 1 A
2 24 Lote1 2 B
3 10 Lote1 3 C
4 18 Lote1 4 D
5 21 Lote1 5 E
6 21 Lote2 1 B
7 26 Lote2 2 C
8 24 Lote2 3 D
9 16 Lote2 4 E
10 20 Lote2 5 F
11 20 Lote3 1 C
12 16 Lote3 2 D
13 19 Lote3 3 E
14 18 Lote3 4 F
15 16 Lote3 5 A
16 22 Lote4 1 D
17 15 Lote4 2 E
18 14 Lote4 3 F
19 19 Lote4 4 A
20 27 Lote4 5 B
21 15 Lote5 1 E
22 13 Lote5 2 F
23 17 Lote5 3 A
24 25 Lote5 4 B
25 21 Lote5 5 C
26 17 Lote6 1 F
27 11 Lote6 2 A
28 12 Lote6 3 B
29 22 Lote6 4 C
30 14 Lote6 5 D
A continuación debemos transformar tanto la columna de los tratamiento como la de los bloques en un factor para podemos realizar los cálculos posteriores adecuadamente.
> youden$Lote <- factor(youden$Lote)
> youden$Concentraciones <- factor(youden$Concentraciones)
> youden$Tiempo_de_reposo <- factor(youden$Tiempo_de_reposo)
Para cada factor realizamos una tabla ANOVA:
- Factor principal:
Para evaluar el efecto de los tratamientos, la suma de cuadrados de tratamientos debe ajustarse por bloques, por lo tanto primero se introducen los bloques y después los tratamientos.
Para calcular la tabla ANOVA hacemos uso de la función “aov” (asume suma de cuadrados tipo I) de la siguiente forma:
> mod1 <- aov(Observaciones~ Tiempo_de_reposo + Lote + Concentraciones, data = youden )
> mod1
Call:
aov(formula = Observaciones ~ Tiempo_de_reposo + Lote + Concentraciones,
data = youden)
Terms:
Tiempo_de_reposo Lote Concentraciones Residuals
Sum of Squares 151.76667 112.73333 61.66667 282.00000
Deg. of Freedom 5 5 4 15
Residual standard error: 4.335897
Estimated effects may be unbalanced
> summary(mod1)
Df Sum Sq Mean Sq F value Pr(>F)
Tiempo_de_reposo 5 151.77 30.35 1.615 0.216
Lote 5 112.73 22.55 1.199 0.356
Concentraciones 4 61.67 15.42 0.820 0.532
Residuals 15 282.00 18.80
donde:
- Observaciones: Nombre de la columna de las observaciones.
- Lote: Nombre de la columna en la que están representados los tratamientos.
- Concentraciones: Nombre de la columna en la que está representado el primer factor bloque.
- Tiempo_de_reposo: Nombre de la columna en la que está representado el segundo factor bloque (letras latinas).
- data = data.frame en el que están guardados los datos.
El p-valor, 0.532, es mayor que el nivel de significación del 5%, deducimos que el factor principal: Concentraciones no es significativo.
- Factor Bloque: Lotes.
Para evaluar el efecto del primero de los bloques, la suma de cuadrados de bloques debe ajustarse por los tratamientos, por lo tanto primero se introducen los tratamientos y después los bloques:
> mod2 <- aov(Observaciones~ Concentraciones +Tiempo_de_reposo + Lote , data = youden )
> mod2
Call:
aov(formula = Observaciones ~ Concentraciones + Tiempo_de_reposo +
Lote, data = youden)
Terms:
Concentraciones Tiempo_de_reposo Lote Residuals
Sum of Squares 61.66667 151.76667 112.73333 282.00000
Deg. of Freedom 4 5 5 15
Residual standard error: 4.335897
Estimated effects may be unbalanced
> summary(mod2)
Df Sum Sq Mean Sq F value Pr(>F)
Concentraciones 4 61.67 15.42 0.820 0.532
Tiempo_de_reposo 5 151.77 30.35 1.615 0.216
Lote 5 112.73 22.55 1.199 0.356
Residuals 15 282.00 18.80
El p-valor, 0.356, es mayor que el nivel de significación del 5%, deducimos que el Factor Bloque: Lotes no es significativo.
- Factor Bloque:Tiempo_de_reposo
Para evaluar el efecto del segundo bloque, la suma de cuadrados de bloques debe ajustarse también por los tratamientos, por lo tanto primero se introducen los tratamientos y después los bloques:
> mod3 <- aov(Observaciones~ Concentraciones + Lote +Tiempo_de_reposo , data = youden )
> mod3
Call:
aov(formula = Observaciones ~ Concentraciones + Lote + Tiempo_de_reposo,
data = youden)
Terms:
Concentraciones Lote Tiempo_de_reposo Residuals
Sum of Squares 61.66667 111.36667 153.13333 282.00000
Deg. of Freedom 4 5 5 15
Residual standard error: 4.335897
Estimated effects may be unbalanced
> summary(mod3)
Df Sum Sq Mean Sq F value Pr(>F)
Concentraciones 4 61.67 15.42 0.820 0.532
Lote 5 111.37 22.27 1.185 0.362
Tiempo_de_reposo 5 153.13 30.63 1.629 0.213
Residuals 15 282.00 18.80
El p-valor es 0.213; mayor que el nivel de significación del 5%, deducimos que Factor Bloque:Tiempo_de_reposo no es significativo.
Diseños Factoriales
En muchos experimentos es frecuente considerar dos o más factores y estudiar el efecto conjunto que dichos factores producen sobre la variable respuesta. Para resolver esta situación se utiliza el Diseño Factorial.
Se entiende por diseño factorial aquel diseño en el que se investigan todas las posibles combinaciones de los niveles de los factores en cada réplica del experimento. En estos diseños, los factores que intervienen tienen la misma importancia a priori y se supone por tanto, la posible presencia de interacción. En este epígrafe vamos a considerar únicamente modelos de efectos fijos.
Diseños factoriales con dos factores
En primer lugar vamos a estudiar los diseños más simples, es decir aquellos en los que intervienen sólo dos factores. Supongamos que hay \( a \) niveles para el factor \( A \) y \( b \) niveles del factor \( B \), cada réplica del experimento contiene todas las posibles combinaciones de tratamientos, es decir contiene los \( ab \) tratamientos posibles.
El modelo sin replicación
El modelo estadístico para este diseño es:
\( y_{ij}=\mu+\tau_i+ \beta_j + (\tau \beta)_{ij} + u_{ij},~~~~ i=1,…,a; ~~~ j=1,…,b ~~~~, ~~~~ \) donde
Expresión 16: Modelo estadístico del diseño factorial de dos factores sin replicación
- \( y_{ij} \): Representa la observación correspondiente al nivel (i) del factor \( A \) y al nivel (j) del factor \( B \).
-
\( \mu \): Efecto constante, común a todos los niveles de los factores, denominado media global.
-
\( \tau_i \): Efecto producido por el nivel i-ésimo del factor \( A \), ( \( \sum_i \tau_i = 0 \)).
-
\( \beta_j \): Efecto producido por el nivel j-ésimo del factor \( B \), \( \sum_j \beta_j = 0 \) ).
-
\( (\tau \beta)_{ij} \): Efecto producido por la interacción entre \( A \times B \), ( \( \sum_i (\tau \beta)_{ij} = \sum_j (\tau \beta)_{ij} = 0 \) ).
-
\( u_{ij} \) son vv aa. independientes con distribución N(0,σ).
Supondremos que se toma una observación por cada combinación de factores, por tanto, hay un total de \( N = ab \) observaciones.
Parámetros a estimar:
\( \begin{array} {|c|c|} \hline \text {Parámetros} & \text {Número} \\ \hline \mu & 1 \\ \hline \tau_i & a-1 \\ \hline \beta_j & b-1 \\ \hline (\tau \beta)_{ij} & (a-1)(b-1) \\ \hline \sigma^2 & 1 \\ \hline Total &ab -1 \\ \hline \end{array} \)
Figura 16: Tabla del número de parámetros a estimar
A pesar de las restricciones impuestas al modelo,
\( \sum_i \tau_i = \sum_j \beta_j = \sum_i (\tau \beta)_{ij} = \sum_j (\tau \beta)_{ij} = 0 \)
el número de parámetros \( (ab + 1) \) supera al número de observaciones \( (ab) \). Por lo tanto, algún parámetro no será estimable.
Los residuos de este modelo son nulos, \( e_{ij} = 0 \), por lo tanto no es posible estimar la varianza del modelo y no se pueden contrastar la significatividad de los efectos de los factores. Dichos contrates sólo pueden realizarse si:
- Suponemos que la interacción entre \( A \times B \) es cero.
- Replicamos el experimento (Tomamos varias observaciones por cada combinación de factores).
Supuesto práctico 8
En unos laboratorios se está investigando sobre el tiempo de supervivencia de unos animales a los que se les suministra al azar tres tipos de venenos y cuatro antídotos distintos. Se pretende estudiar si los tiempos de supervivencia de los anímales varían en función de las combinaciones veneno-antídoto. Los datos que se recogen en la tabla adjunta son los tiempos de supervivencia en horas.
\( \begin{array} {|l|c|c|c|c|} \hline \text { Veneno} & \text {Antídoto 1} & \text {Antídoto 2 } & \text {Antídoto 3} & \text {Antídoto 4} \\ \hline \text {Veneno 1 } & 4.5 & 11.0 & 4.5 & 7.1 \\ \hline \text {Veneno 2 } & 2.9 & 6.1 & 3.5 & 10.2 \\ \hline \text {Veneno 3 } & 2.1 & 3.7 & 2.5 & 3.6 \\ \hline \end{array} \)
Figura 17: Tabla de datos del Supuesto Práctico 8.doc
El objetivo principal es estudiar la influencia de tres tipos de venenos y 4 tipos de antídotos en el tiempo de supervivencia de unos determinados animales, por lo que se trata de un modelo con dos factores: el veneno (con tres niveles) y el antídoto (con cuatro niveles). La variable que va a medir las diferencias entre los tratamientos es el tiempo que sobreviven los animales. Se combinan todos los niveles de los dos factores por lo que tenemos en total doce tratamientos.
- Variable respuesta: Tiempo de supervivencia
- Factor: Tipo de veneno que tiene tres niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Factor: Tipo de antídoto que tiene cuatro niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Tamaño del experimento: Número total de observaciones (12).
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto:
 Figura 18: Tabla de datos del Supuesto Práctico 8.txt
Figura 18: Tabla de datos del Supuesto Práctico 8.txt
Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en la imagen, es decir, las observaciones en una sola columna y a continuación especificado sus factores correspondientes.
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
> setwd(“C:/Users/Usuario/Desktop/Datos”)
> factorial <- read.table(“laboratorio.txt”, header = TRUE)
> factorial
Tiempo Veneno Antidoto
1 4.5 1 1
2 2.9 2 1
3 2.1 3 1
4 11.0 1 2
5 6.1 2 2
6 3.7 3 2
7 4.5 1 3
8 3.5 2 3
9 2.5 3 3
10 7.1 1 4
11 10.2 2 4
12 3.6 3 4
A continuación debemos transformar todas las columnas que contienen a los factores en un factor para podemos realizar los cálculos posteriores adecuadamente.
> factorial$Antidoto <- factor(factorial$Antidoto)
> factorial$Veneno <- factor(factorial$Veneno)
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma
> mod <- aov(Tiempo~ Veneno + Antidoto , data = factorial )
> mod
Call:
aov(formula = Tiempo ~ Veneno + Antidoto, data = factorial)
Terms:
Veneno Antidoto Residuals
Sum of Squares 30.58667 39.40917 23.89333
Deg. of Freedom 2 3 6
Residual standard error: 1.995551
Estimated effects may be unbalanced
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
> summary(mod)
Df Sum Sq Mean Sq F value Pr(>F)
Veneno 2 30.59 15.293 3.840 0.0844 .
Antidoto 3 39.41 13.136 3.299 0.0995 .
Residuals 6 23.89 3.982
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Esta Tabla ANOVA recoge la descomposición de la varianza considerando como fuente de variación los doce tratamientos o grupos que se forman al combinar los niveles de los dos factores. Mediante esta tabla se puede estudiar sí varían los tiempos que sobreviven los animales en función de las combinaciones veneno-antídoto. Es decir, se pueden estudiar si existen diferencias significativas entre los tiempos medios de supervivencia con los distintos tipos de venenos y antídotos, pero no se puede estudiar si la efectividad de los antídotos es la misma para todos los venenos. Observando los p-valores, 0.084 y 0.099; mayores respectivamente que el nivel de significación del 5%, deducimos que ningún efecto es significativo. Por lo tanto, no existen diferencias en los tiempos medios de supervivencia de los animales, en función de la pareja veneno-antídoto que se les suministra.
El modelo con replicación
El modelo estadístico para este diseño es:
\( y_{ijk}=\mu+\tau_i+ \beta_j + (\tau \beta)_{ij} + u_{ijk},~~~~ i=1,…,a; ~~~ j=1,…,b, ~~~k=1,…,r ~~~~, ~~~~ \) donde
Expresión 17: Modelo estadístico del diseño factorial de dos factores con replicación
donde \( r \) es el número de replicaciones y \( N = abr \) es el número de observaciones.
El número de parámetros de este modelo es, como en el modelo de dos factores sin replicación, \( ab+1 \) pero en este caso el número de observaciones es \( abr \).
La descripción del diseño así como la terminología subyacente la vamos a introducir mediante el siguiente supuesto práctico.
Supuesto práctico 9
Consideremos el supuesto práctico anterior en el que realizamos dos réplicas por cada tratamiento. Los datos que se recogen en la tabla adjunta son los tiempos de supervivencia en horas de unos animales a los que se les suministra al azar tres venenos y cuatro antídotos. El objetivo es estudiar qué antídoto es el adecuado para cada veneno.
\( \begin{array} {|l|c|c|c|c|} \hline \text { Veneno} & \text {Antídoto 1} & \text {Antídoto 2 } & \text {Antídoto 3} & \text {Antídoto 4} \\ \hline \text {Veneno 1 } & 4.5 & 11.0 & 4.5 & 7.1 \\ & 4.3 & 7.2 & 7.6 & 6.2 \\ \hline \text {Veneno 2 } & 2.9 & 6.1 & 3.5 & 10.2 \\ & 2.3 & 12.4 & 4.0 & 3.8 \\ \hline \text {Veneno 3 } & 2.1 & 3.7 & 2.5 & 3.6 \\ & 2.3 & 2.9 & 2.2 & 3.3 \\ \hline \end{array} \)
Figura 19: Tabla de datos del Supuesto Práctico 9.doc
El modelo matemático que planteamos es el siguiente:
\( y_{ijk}=\mu+\tau_i+ \beta_j + (\tau \beta)_{ij} + u_{ijk},~~~~ i=1, 2, 3; ~~~ j=1, 2, 3, 4; ~~~k=1, 2; \)
donde
- \( y_{ijk}\) : Representa el tiempo de supervivencia del animal \( k \) al que se le suministró el veneno \( i \) y el antídoto \( j \).
- \( \mu \): Efecto constante, común a todos los niveles de los factores, denominado media global.
- \( \tau_i \): Efecto medio producido por el veneno i, \( (\sum_i \tau_i = 0 ) \).
- \( \beta_j \): Efecto medio producido por antídoto j, \( (\sum_j \beta_j = 0 ) \).
- \( (\tau \beta)_{ij} \): Efecto medio producido por la interacción entre el veneno i y el antídoto j, \( (\sum_i (\tau \beta)_{ij} = \sum_j (\tau \beta)_{ij} = 0) \).
- \( u_{ijk} \): Vv aa. independientes con distribución \( N(0,σ) \).
- Variable respuesta: Tiempo de supervivencia;
- Factor: Tipo de veneno (tres niveles).
- Factor: Tipo de antídoto (cuatro niveles).
- Ambos factores de efectos fijos.
- Tamaño del experimento: Número total de observaciones (24).
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto:

Figura 20: Tabla de datos del Supuesto Práctico 9.txt
Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en la imagen, es decir, las observaciones en una sola columna y a continuación especificado sus factores correspondientes.
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
> setwd(“C:/Users/Usuario/Desktop/Datos”)
> factorial <- read.table(“laboratorio2.txt”, header = TRUE)
> factorial
Tiempo Veneno Antidoto
1 4.5 1 1
2 4.3 1 1
3 2.9 2 1
4 2.3 2 1
5 2.1 3 1
6 2.3 3 1
7 11.0 1 2
8 7.2 1 2
9 6.1 2 2
10 12.4 2 2
11 3.7 3 2
12 2.9 3 2
13 4.5 1 3
14 7.6 1 3
15 3.5 2 3
16 4.0 2 3
17 2.5 3 3
18 2.2 3 3
19 7.1 1 4
20 6.2 1 4
21 10.2 2 4
22 3.8 2 4
23 3.6 3 4
24 3.3 3 4
A continuación debemos transformar todas las columnas que contienen a los factores en un factor para podemos realizar los cálculos posteriores adecuadamente.
> factorial$Veneno <- factor(factorial$Veneno)
> factorial$Antidoto <- factor(factorial$Antidoto)
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
> mod <- aov(Tiempo~ Veneno * Antidoto , data = factorial )
> mod
Call:
aov(formula = Tiempo ~ Veneno * Antidoto, data = factorial)
Terms:
Veneno Antidoto Veneno:Antidoto Residuals
Sum of Squares 60.44333 60.26167 20.36333 53.51000
Deg. of Freedom 2 3 6 12
Residual standard error: 2.111674
Estimated effects may be unbalanced
> summary(mod)
Df Sum Sq Mean Sq F value Pr(>F)
Veneno 2 60.44 30.222 6.777 0.0107 *
Antidoto 3 60.26 20.087 4.505 0.0245 *
Veneno:Antidoto 6 20.36 3.394 0.761 0.6138
Residuals 12 53.51 4.459
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
La Tabla ANOVA muestra las filas de Tipo_veneno, Tipo_antídoto y Tipo_veneno*Tipo_antídoto que corresponde a la variabilidad debida a los efectos de cada uno de los factores y de la interacción entre ambos.
Las preguntas que nos planteamos son: ¿Los venenos son igual de peligrosos? ¿Y los antídotos son igual de efectivos? La efectividad de los antídotos, ¿es la misma para todos los venenos? Para responder a estas preguntas, comenzamos comprobando si el efecto de los antídotos es el mismo para todos los venenos. Para ello observamos el valor del estadístico (Fexp= 0.761) que contrasta la hipótesis correspondiente a la interacción entre ambos factores (H0: (τβ)ij = 0). Dicho valor deja a la derecha un Sig. = 0.614, mayor que el nivel de significación 0.05. Por lo tanto la interacción entre ambos factores no es significativa y debemos eliminarla del modelo. Construimos de nuevo la Tabla ANOVA en la que sólo figurarán los efectos principales
> mod <- aov(Tiempo~ Veneno + Antidoto , data = factorial )
> mod
Call:
aov(formula = Tiempo ~ Veneno + Antidoto, data = factorial)
Terms:
Veneno Antidoto Residuals
Sum of Squares 60.44333 60.26167 73.87333
Deg. of Freedom 2 3 18
Residual standard error: 2.025851
Estimated effects may be unbalanced
> summary(mod)
Df Sum Sq Mean Sq F value Pr(>F)
Veneno 2 60.44 30.222 7.364 0.0046 **
Antidoto 3 60.26 20.087 4.894 0.0117 *
Residuals 18 73.87 4.104
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Esta tabla muestra dos únicas fuentes de variación, lo efectos principales de los dos factores (Tipo_veneno y Tipo_antídoto), y se ha suprimido la interacción entre ambos. Se observa que el valor de la Suma de Cuadrados del error de este modelo (73.873) se ha formado con los valores de las Sumas de cuadrados del error y de la interacción del modelo anterior (20.363 + 53.510 = 73.873). Observando los valores de los p-valores, 0.0046 y 0.0117 asociados a los contrastes principales, se deduce que los dos efectos son significativos a un nivel de significación del 5%. Deducimos que ni la gravedad de los venenos es la misma, ni la efectividad de los antídotos, pero dicha efectividad no depende del tipo de veneno con el que se administre ya que la interacción no es significativa.
Diseños factoriales con tres factores
Supongamos que hay \( a \) niveles para el factor \( A \), \( b \) niveles del factor \( B \) y \( c \) niveles para el factor \( C \) y que cada réplica del experimento contiene todas las posibles combinaciones de tratamientos, es decir contiene los \( abc \) tratamientos posibles.
El modelo sin replicación
El modelo estadístico para este diseño es:
\( y_{ijk}=\mu+\tau_i+ \beta_j + \gamma_k + (\tau \beta)_{ij} + (\tau \gamma)_{ik} + (\beta \gamma)_{jk}+ (\tau \beta \gamma)_{ijk} + u_{ijk},~~~~ i=1,…,a; ~~~ j=1,…,b, ~~~k=1,…,c ~~~~, ~~~~ \)
Expresión 19: Modelo estadístico del diseño factorial de tres factores sin replicación
donde
- \( y_{ijk} \): Representa la observación correspondiente al nivel (i) del factor \( A \), al nivel (j) del factor \( B \) y al nivel (k) del factor \( C \).
-
\( \mu \): Efecto constante, común a todos los niveles de los factores, denominado media global.
-
\( \tau_i \): Efecto producido por el nivel i-ésimo del factor \( A \), ( \( \sum_i \tau_i = 0 \)).
-
\( \beta_j \): Efecto producido por el nivel j-ésimo del factor \( B \), \( \sum_j \beta_j = 0 \) ).
-
\( \gamma_k \): Efecto producido por el nivel k-ésimo del factor \( C \), \( \sum_k \gamma_k = 0 \) ).
-
\( (\tau \beta)_{ij} \): Efecto producido por la interacción entre \( A \times B \), ( \( \sum_i (\tau \beta)_{ij} = \sum_j (\tau \beta)_{ij} = 0 \) ).
-
\( (\tau \gamma)_{ik} \): Efecto producido por la interacción entre \( A \times C \), ( \( \sum_i (\tau \gamma)_{ik} = \sum_k (\tau \gamma)_{ik} = 0 \) ).
-
\( (\beta \gamma)_{jk} \): Efecto producido por la interacción entre \( B \times C \), ( \( \sum_j (\beta \gamma)_{jk} = \sum_k (\beta \gamma)_{jk} = 0 \) ).
-
\( (\tau \beta \gamma)_{ijk} \): Efecto producido por la interacción entre \( A \times B \times C \), ( \( \sum_i (\tau \beta \gamma)_{ijk} = \sum_j (\tau \beta \gamma)_{ijk} = \sum_k (\tau \beta \gamma)_{ijk} = 0 \) ).
-
\( u_{ij} \) son vv aa. independientes con distribución N(0,σ).
Supondremos que se toma una observación por cada combinación de factores, por tanto, hay un total de \( N = ab c \) observaciones.
Parámetros a estimar:
\( \begin{array} {|c|c|} \hline \text {Parámetros} & \text {Número} \\ \hline \mu & 1 \\ \hline \tau_i & a-1 \\ \hline \beta_j & b-1 \\ \hline \gamma_k & c-1 \\ \hline (\tau \beta)_{ij} & (a-1)(b-1) \\ \hline (\tau \gamma)_{ij} & (a-1)(c-1) \\ \hline ( \beta \gamma)_{jk} & (b-1)(c-1) \\ \hline (\tau \beta \gamma)_{ijk} & (a-1)(b-1)(c-1) \\ \hline \sigma^2 & 1 \\ \hline Total & abc +11 \\ \hline \end{array} \)
Figura 21: Tabla del número de parámetros a estimar
A pesar de las restricciones impuestas al modelo,
\( \sum_i \tau_i = \sum_j \beta_j = \sum_k \gamma_k = \sum_i (\tau \beta)_{ij} = \sum_j (\tau \beta)_{ij}= , \cdots , = \sum_k (\tau \beta \gamma)_{ijk} = 0 \)
el número de parámetros \( (abc + 1) \) supera al número de observaciones \( (abc) \). Por lo tanto, algún parámetro no será estimable.
Expresión de la descomposición de la variabilidad de la variable respuesta.
\( SCT=SCA+SCB+SCC+SC(AB)+SC(AC)+SC(BC)+SC(ABC)+SCR \)
Que representan:
- \( SCT \) : Suma de Cuadrados Total,
- \( SCA, SCB, SCC \): Suma de Cuadrados entre los niveles de \( A \), de \( B \) y de \( C \), respectivamente
- \( SC(AB), SC(AC), SC(BC), SC(ABC), SCR \): Suma de Cuadrados de las interacciones \( A×B, A×C, B×C, A×B×C \) y del error, respectivamente.
A partir de la ecuación básica del Análisis de la Varianza se pueden construir los cuadrados medios definidos como:
-
Cuadrado medio total: \( CMT=(SCT)/(n-1) \)
-
Cuadrado medio de \( A \) : \( CMA=(SCA)/(a-1) \)
-
Cuadrado medio de \( B \) : \( CMB=(SCB)/(b-1) \)
-
Cuadrado medio de \( C \) : \( CMC=(SCC)/(c-1) \)
-
Cuadrado medio de las interacciones:
-
Cuadrado medio residual: \(CMR=(SCR)/((a-1)(b-1(c-1)) \)
Supuesto práctico 10
En una fábrica de refrescos está haciendo unos estudios en la planta embotelladora. El objetivo es obtener más uniformidad en el llenado de las botellas. La máquina de llenado teóricamente llena cada botella a la altura correcta, pero en la práctica hay variación, y la embotelladora desea entender mejor las fuentes de esta variabilidad para eventualmente reducirla. En el proceso se pueden controlar tres factores durante el proceso de llenado: El % de carbonato (factor A), la presión del llenado (factor B) y el número de botellas llenadas por minuto que llamaremos velocidad de la línea (factor C). Se consideran tres niveles para el factor A (10%, 12%, 14%), dos niveles para el factor B (25psi, 30psi) y dos niveles para el factor C (200bpm, 250bpm). Los datos recogidos de la desviación de la altura objetivo se muestran en la tabla adjunta
\( \begin{array} {|c|cc|cc|} \hline & \text {Presión } & & \text {Presión } \\ \hline & \text {25 psi } & & \text {30 psi}& \\ \hline & \text {Velocidad } & & \text {Velocidad } \\ \hline \text {% de Carbono } & 200 & 250 & 200 & 250 \\ \hline 10 & 10 & 3 & 5 & -1 \\ \hline 12 & 11 & 2 & 5 & -3 \\ \hline 14 & 2 & 4 & -3 & 1 \\ \hline \end{array} \)
Figura 22: Tabla de datos del Supuesto Práctico10.doc
Analizar los resultados y obtener las conclusiones apropiadas.
El modelo matemáticos que planteamos es el Modelo del diseño factorial de tres factores sin replicación siguiente:
\( y_{ijk}=\mu+\tau_i+ \beta_j + \gamma_k + (\tau \gamma)_{ik} + (\beta \gamma)_{jk} + u_{ijk},~~~~ i=1,2,3; ~~~ j=1,2; ~~~ k =1,2 \)
Expresión 20: Diseño Factorial de tres factores sin replicación (Supuesto práctico 10)
donde
- \( y_{ijk} \): Representa la desviación de la altura objetivo en la botella al porcentaje i de carbono, a la concentración j y a la velocidad k.
-
\( \mu \): Efecto constante, común a todos los niveles de los factores, denominado media global.
-
\( \tau_i \): Efecto medio producido por el tanto por ciento i de carbono.
-
\( \beta_j \): Efecto medio producido por la presión j.
-
\( \gamma_k \): Efecto producido por la velocidad k.
-
\( (\tau \beta)_{ij} \): Efecto medio producido por la interacción entre el porcentaje i de carbono y la presión j.
-
\( (\tau \gamma)_{ik} \): Efecto producido por la interacción entre \( A \times C \), ( \( \sum_i (\tau \gamma)_{ik} = \sum_k (\tau \gamma)_{ik} = 0 \) ).
-
\( (\beta \gamma)_{jk} \): Efecto producido por la interacción entre la presión j y la velocidad k.
-
\( (\tau \beta \gamma)_{ijk} \): Efecto producido por la interacción entre el porcentaje i de carbono, la presión j y la velocidad k.
-
\( u_{ij} \) son vv aa. independientes con distribución N(0,σ).
-
Estos efectos son parámetros a estimar, con las condiciones : \( \sum_i \tau_i = \sum_j \beta_j = \sum_k \gamma_k = \sum_i (\tau \beta)_{ij} = \cdots = \sum_k (\beta \gamma)_{jk} =0 \)
La variable respuesta de este experimento es la Desviación que se produce en la altura de llenado en las botellas de refresco, siendo dichas botellas las unidades experimentales. En estas desviaciones de la altura de llenado marcada como objetivo intervienen tres factores: Porcentaje de carbono que presenta tres niveles 10%, 12% y 14%; Presión, con dos niveles 25 psi y 30 psi y Velocidad, con dos niveles 200 y 250. Los niveles de los factores han sido fijados por el experimentador, por lo que todos los factores son de efectos fijos. Se trata de un diseño trifactorial de efectos fijos, donde el número de tratamientos es 3×2×2 = 12.
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto:
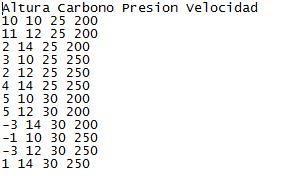
Figura 23: Tabla de datos del Supuesto Práctico10.txt
Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en la imagen, es decir, las observaciones en una sola columna y a continuación especificado sus factores correspondientes.
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
> setwd(“C:/Users/Usuario/Desktop/Datos”)
> factorial <- read.table(“embotelladora.txt”, header = TRUE)
> factorial
Altura Carbono Presion Velocidad
1 10 10 25 200
2 11 12 25 200
3 2 14 25 200
4 3 10 25 250
5 2 12 25 250
6 4 14 25 250
7 5 10 30 200
8 5 12 30 200
9 -3 14 30 200
10 -1 10 30 250
11 -3 12 30 250
12 1 14 30 250
A continuación debemos transformar la tres columnas en factores para poder realizar los cálculos posteriores adecuadamente.
> factorial$Carbono <- factor(factorial$Carbono)
> factorial$Velocidad <- factor(factorial$Velocidad)
> factorial$Presion <- factor(factorial$Presion)
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
> mod <- aov(Altura~ Carbono + Presion + Velocidad + Carbono*Presion + Carbono*Velocidad + Presion*Velocidad , data = factorial )
donde:
- Altura: Nombre de la columna de las observaciones
- Carbono: Nombre de la columna en la que está representado el primer factor
- Presion: Nombre de la columna en la que está representado el segundo factor
- Velocidad: Nombre de la columna en la que está representado el tercer factor
- Carbono*Presion, Carbono*Velocidad y Presion*Velocidad hace referencia a las distintas interacciones.
- data= data.frame en el que están guardados los datos
> mod
Call:
aov(formula = Altura ~ Carbono + Presion + Velocidad + Carbono *
Presion + Carbono * Velocidad + Presion * Velocidad, data = factorial)
Terms:
Carbono Presion Velocidad Carbono:Presion Carbono:Velocidad
Sum of Squares 24.50000 65.33333 48.00000 1.16667 75.50000
Deg. of Freedom 2 1 1 2 2
Presion:Velocidad Residuals
Sum of Squares 1.33333 0.16667
Deg. of Freedom 1 2
Residual standard error: 0.2886751
Estimated effects may be unbalanced
> summary(mod)
Df Sum Sq Mean Sq F value Pr(>F)
Carbono 2 24.50 12.25 147 0.00676 **
Presion 1 65.33 65.33 784 0.00127 **
Velocidad 1 48.00 48.00 576 0.00173 **
Carbono:Presion 2 1.17 0.58 7 0.12500
Carbono:Velocidad 2 75.50 37.75 453 0.00220 **
Presion:Velocidad 1 1.33 1.33 16 0.05719 .
Residuals 2 0.17 0.08
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
La Tabla ANOVA muestra las filas de Carbono, Presión, Velocidad, Carbono*Presión, Carbono*Velocidad y Presión*Velocidad que corresponden a la variabilidad debida a los efectos de cada uno de los factores y a las interacciones de orden dos entre ambos. En dicha Tabla se indica que para un nivel de significación del 5% los efectos que no son significativos del modelo planteado son las interacciones entre los factores Carbono*Presión y Presión*Velocidad ya que los p-valores correspondientes a estos efectos son 0.125 y 0.057 mayores que el nivel de significación.
Como consecuencia de este resultado, replanteamos el modelo suprimiendo en primer lugar el efecto Carbono*Presión, cuya significación es mayor, y resulta el siguiente modelo matemático:
\( y_{ijk}=\mu+\tau_i+ \beta_j + \gamma_k + (\tau \gamma)_{ik} + (\beta \gamma)_{jk} + u_{ijk},~~~~ i=1,2,3; ~~~ j=1,2; ~~~ k =1,2 \)
donde los efectos deben cumplir las condiciones expuestas anteriormente. Para resolverlo suprimimos la interacción Carbono*Presión. La tabla ANOVA que corresponde a este modelo es la siguiente:
> mod <- aov(Altura~ Carbono + Presion + Velocidad + Carbono*Velocidad + Presion*Velocidad , data = factorial )
> summary(mod)
Df Sum Sq Mean Sq F value Pr(>F)
Carbono 2 24.50 12.25 36.75 0.002664 **
Presion 1 65.33 65.33 196.00 0.000151 ***
Velocidad 1 48.00 48.00 144.00 0.000276 ***
Carbono:Velocidad 2 75.50 37.75 113.25 0.000301 ***
Presion:Velocidad 1 1.33 1.33 4.00 0.116117
Residuals 4 1.33 0.33
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
El efecto Presión*Velocidad sigue siendo no significativo por lo que lo suprimimos del modelo y replanteamos el siguiente modelo matemático
\( y_{ijk}=\mu+\tau_i+ \beta_j + \gamma_k + (\tau \gamma)_{ik} + u_{ijk},~~~~ i=1,2,3; ~~~ j=1,2, ~~~k=1,2 \)
donde los efectos deben cumplir las condiciones expuestas anteriormente. Para resolverlo suprimimos la interacción Presión*Velocidad. La tabla ANOVA que corresponde a este modelo es la siguiente:
> mod <- aov(Altura~ Carbono + Presion + Velocidad + Carbono*Velocidad, data = factorial )
> summary(mod)
Df Sum Sq Mean Sq F value Pr(>F)
Carbono 2 24.50 12.25 22.97 0.003019 **
Presion 1 65.33 65.33 122.50 0.000105 ***
Velocidad 1 48.00 48.00 90.00 0.000220 ***
Carbono:Velocidad 2 75.50 37.75 70.78 0.000215 ***
Residuals 5 2.67 0.53
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Todos los efectos de este último modelo planteado son significativos y por lo tanto es en este modelo donde vamos a realizar el estudio. Existen diferencias significativas entre los distintos porcentajes del Carbono, los dos tipos de presión, las dos velocidades de llenado y la interacción entre el porcentaje de Carbono y la Velocidad de llenado.
El modelo con replicación
El modelo estadístico para este diseño es:
\( y_{ijkl}=\mu+\tau_i+ \beta_j + \gamma_k + (\tau \beta)_{ij} + (\tau \gamma)_{ik} + (\beta \gamma)_{jk}+ (\tau \beta \gamma)_{ijk} + u_{ijkl},~~~~ i=1,…,a; ~~~ j=1,…,b, ~~~k=1,…,c ~~~~, l = 1,2,…,r \)
Expresión 22: Modelo estadístico del diseño factorial de tres factores con replicación
donde r es el número de replicaciones y \( N=abcr \) y es el número de observaciones. El número de parámetros de este modelo es, como en el modelo de tres factores sin replicación, \( abc + 1 \) pero en este caso el número de observaciones es \( abcr \). El objetivo del análisis de este modelo es realizar los contrastes sobre los efectos principales, las interacciones de orden dos y la interacción de orden tres.
Supuesto práctico 11
Consideremos el supuesto práctico anterior en el que realizamos dos réplicas por cada tratamiento. En la Tabla adjunta se muestran los datos recogidos de la desviación de la altura objetivo de las botellas de refresco. En el proceso de llenado, la embotelladora puede controlar tres factores durante el proceso: El porcentaje de carbonato (factor A) con tres niveles (10%, 12%, 14%), la presión del llenado (factor B) con dos niveles (25psi, 30psi) y el número de botellas llenadas por minuto que llamaremos velocidad de la línea (factor C) con dos niveles (200bpm, 250bpm).
\( \begin{array} {|c|cc|cc|} \hline & \text {Presión } & & \text {Presión } \\ \hline & \text {25 psi } & & \text {30 psi}& \\ \hline & \text {Velocidad } & & \text {Velocidad } \\ \hline \text {% de Carbono } & 200 & 250 & 200 & 250 \\ \hline 10 & 10 & 3 & 5 & -1 \\ & 20 & 5 & 9 & -3 \\ \hline 12 & 11 & 2 & 5 & -3 \\ & 9 & 5 & 4 & 2 \\ \hline 14 & 2 & 4 & -3 & 1 \\ & -1 & 7 & -2 & 3 \\ \hline \end{array} \)
Figura 24: Tabla de datos del Supuesto Práctico11.doc
El modelo matemáticos del experimento que planteamos es el siguiente:
\( y_{ijkl}=\mu+\tau_i+ \beta_j + \gamma_k + (\tau \beta)_{ij} + (\tau \gamma)_{ik} + (\beta \gamma)_{jk}+ (\tau \beta \gamma)_{ijk} + u_{ijkl},~~~~ i=1,2,3; ~~~ j=1,2; ~~~k=1,2; ~~~~, l = 1,2 \)
La variable respuesta y los efectos de los factores se definieron en el Supuesto práctico 10. Las restricciones para este modelo son: \( \sum_i \tau_i = \sum_j \beta_j = \sum_k \gamma_k = \sum_i (\tau \beta)_{ij} = \cdots = \sum_k (\tau \beta \gamma)_{ijk} =0 \).
La variable respuesta de este experimento es la Desviación que se produce de la altura objetivo en el llenado en las botellas de refresco. Los factores son: Porcentaje de Carbono que presenta tres niveles 10%, 12% y 14%; Presión, con dos niveles 25 psi y 30 psi y Velocidad, con dos niveles 200 y 250. Los niveles de los factores han sido fijados por el experimentador, por lo que todos los factores son de efectos fijos. Se trata de un diseño trifactorial de efectos fijos, donde el número de tratamientos es 3×2×2 = 12 y el número de observaciones 24.
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto:

Figura 25: Tabla de datos del Supuesto Práctico11.txt
Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en la imagen, es decir, las observaciones en una sola columna y a continuación especificado sus factores correspondientes.
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
> setwd(“C:/Users/Usuario/Desktop/Datos”)
> factorial <- read.table(“embotelladora2.txt”, header = TRUE)
> factorial
Altura Carbono Presion Velocidad
1 10 10 25 200
2 20 10 25 200
3 11 12 25 200
4 9 12 25 200
5 2 14 25 200
6 -1 14 25 200
7 3 10 25 250
8 5 10 25 250
9 2 12 25 250
10 5 12 25 250
11 4 14 25 250
12 7 14 25 250
13 5 10 30 200
14 9 10 30 200
15 5 12 30 200
16 4 12 30 200
17 -3 14 30 200
18 -2 14 30 200
19 -1 10 30 250
20 -3 10 30 250
21 -3 12 30 250
22 2 12 30 250
23 1 14 30 250
24 3 14 30 250
A continuación debemos transformar las tres columnas en factores para poder realizar los cálculos posteriores adecuadamente.
> factorial$Carbono <- factor(factorial$Carbono)
> factorial$Velocidad <- factor(factorial$Velocidad)
> factorial$Presion <- factor(factorial$Presion)
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
> mod <- aov(Altura~ Carbono + Presion + Velocidad + Carbono*Presion + Carbono*Velocidad + Presion*Velocidad + Carbono*Velocidad*Presion, data = factorial )
donde:
- Altura: Nombre de la columna de las observaciones
- Carbono: Nombre de la columna en la que está representado el primer factor
- Presion: Nombre de la columna en la que está representado el segundo factor
- Velocidad: Nombre de la columna en la que está representado el tercer factor
- Carbono*Presion, Carbono*Velocidad, Presion*Velocidad y Carbono*Velocidad*Presion hace referencia a las distintas interacciones.
- data= data.frame en el que están guardados los datos
y posteriormente mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
> summary(mod)
Df Sum Sq Mean Sq F value Pr(>F)
Carbono 2 88.08 44.04 5.683 0.018350 *
Presion 1 150.00 150.00 19.355 0.000866 ***
Velocidad 1 80.67 80.67 10.409 0.007270 **
Carbono:Presion 2 14.25 7.12 0.919 0.425122
Carbono:Velocidad 2 230.58 115.29 14.876 0.000564 ***
Presion:Velocidad 1 1.50 1.50 0.194 0.667799
Carbono:Presion:Velocidad 2 1.75 0.88 0.113 0.894175
Residuals 12 93.00 7.75
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
La Tabla ANOVA muestra las filas de Carbono, Presión, Velocidad, Carbono*Presión, Carbono*Velocidad, Presión*Velocidad y Carbono*Presión*Velocidad que corresponden a la variabilidad debida a los efectos de cada uno de los factores, a las interacciones de orden dos y orden tres entre los factores. En dicha Tabla se indica que para un nivel de significación del 5% los efectos que no son significativos del modelo planteado son las interacciones entre los factores, Carbono*Presión y Presión*Velocidad y Carbono*Presión*Velocidad ya que los p-valores correspondientes a estos efectos son 0.425, 0.668 y 0.894 mayores que el nivel de significación.
Como consecuencia de este resultado, replanteamos el modelo suprimiendo en primer lugar el efecto Carbono*Presión*Velocidad, cuya significación es mayor, y resulta el siguiente modelo matemático:
\( y_{ijkl}=\mu+\tau_i+ \beta_j + \gamma_k + (\tau \beta)_{ij} + (\tau \gamma)_{ik} + (\beta \gamma)_{jk}+ u_{ijkl},~~~~ i=1,2,3; ~~~ j=1,2; ~~~k=1,2; ~~~~, l = 1,2 \)
donde los efectos deben cumplir las condiciones expuestas anteriormente.
Para resolverlo suprimimos la interacción Carbono*Presión*Velocidad. La tabla ANOVA que corresponde a este modelo es la siguiente:
> mod <- aov(Altura~ Carbono + Presion + Velocidad + Carbono*Presion + Carbono*Velocidad + Presion*Velocidad, data = factorial )
> summary(mod)
Df Sum Sq Mean Sq F value Pr(>F)
Carbono 2 88.08 44.04 6.507 0.010038 *
Presion 1 150.00 150.00 22.164 0.000336 ***
Velocidad 1 80.67 80.67 11.919 0.003886 **
Carbono:Presion 2 14.25 7.12 1.053 0.375033
Carbono:Velocidad 2 230.58 115.29 17.035 0.000178 ***
Presion:Velocidad 1 1.50 1.50 0.222 0.645047
Residuals 14 94.75 6.77
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Los efectos Carbono*Presión y Presión*Velocidad siguen siendo no significativos.
Suprimimos el efecto Presión*Velocidad que tiene una no significatividad más alta y replanteamos el siguiente modelo matemático
\( y_{ijkl}=\mu+\tau_i+ \beta_j + \gamma_k + (\tau \beta)_{ij} + (\tau \gamma)_{ik} + u_{ijkl},~~~~ i=1,2,…,a; ~~~ j=1,2,…,b; ~~~k=1,2,…,c; ~~~~, l = 1,2,…,r \)
donde los efectos deben cumplir las condiciones expuestas anteriormente.
Para resolverlo suprimimos la interacción Presión*Velocidad. La tabla ANOVA que corresponde a este modelo es la siguiente:
> mod <- aov(Altura~ Carbono + Presion + Velocidad + Carbono*Presion + Carbono*Velocidad, data = factorial )
> summary(mod)
Df Sum Sq Mean Sq F value Pr(>F)
Carbono 2 88.08 44.04 6.864 0.007647 **
Presion 1 150.00 150.00 23.377 0.000218 ***
Velocidad 1 80.67 80.67 12.571 0.002935 **
Carbono:Presion 2 14.25 7.12 1.110 0.355049
Carbono:Velocidad 2 230.58 115.29 17.968 0.000104 ***
Residuals 15 96.25 6.42
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
El efecto Carbono*Presión sigue siendo no significativo por lo tanto lo suprimimos y replanteamos el siguiente modelo matemático
\( y_{ijk}=\mu+\tau_i+ \beta_j + \gamma_k + (\tau \gamma)_{ik} + u_{ijk},~~~~ i=1,2,3,4; ~~~ j=1,2; ~~~k=1,2,3,4 \)
> mod <- aov(Altura~ Carbono + Presion + Velocidad + Carbono*Velocidad, data = factorial )
> summary(mod)
Df Sum Sq Mean Sq F value Pr(>F)
Carbono 2 88.08 44.04 6.776 0.006856 **
Presion 1 150.00 150.00 23.077 0.000166 ***
Velocidad 1 80.67 80.67 12.410 0.002612 **
Carbono:Velocidad 2 230.58 115.29 17.737 6.91e-05 ***
Residuals 17 110.50 6.50
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Todos los efectos de este último modelo planteado son significativos y por lo tanto es en este modelo donde vamos a realizar el estudio. Existen diferencias significativas entre los distintos porcentajes del Carbono, los dos tipos de presión, las dos velocidades de llenado y la interacción entre el porcentaje de Carbono y la Velocidad de llenado.
Ejercicios
Ejercicios Guiados
Ejercicio Guiado1
Se realiza un estudio del contenido de azufre en cinco yacimientos de carbón. Se toman muestras aleatoriamente de cada uno de los yacimientos y se analizan. Los datos del porcentaje de azufre por muestra se indican en la tabla adjunta.
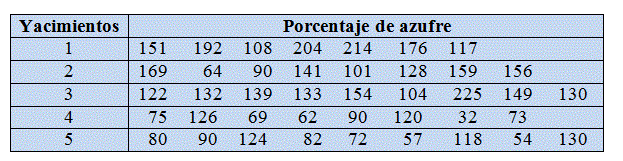 Figura 26: Tabla de datos del Ejercicio Guiado1.doc
Figura 26: Tabla de datos del Ejercicio Guiado1.doc
Para un nivel de significación del 5%.
-
¿Se puede confirmar que el porcentaje de azufre es el mismo en los cinco yacimientos?
-
Si se rechaza la hipótesis nula que las medias de porcentaje de azufre en los cinco yacimientos es la misma, determinar que medias difieren entre sí utilizando el método de comparaciones múltiples de Tukey.
- Estudiar las hipótesis de modelo: Homocedasticidad (Homogeneidad de las varianzas por grupo), Independencia y Normalidad.
Ejercicio Guiado2
Se realiza un estudio sobre el efecto del fotoperiodo y del genotipo en el periodo latente de infección del moho de cebada aislado AB3. Se obtienen cincuenta hojas de cuatro genotipos distintos. Cada grupo es infectado y posteriormente expuesto a diferente fotoperiodo. Los distintos fotoperiodos se trataron como bloques y se obtuvieron los siguientes datos de los totales para los bloques y tratamientos. La respuesta anotada es el número de días hasta la aparición de síntomas visibles.
 Figura 27: Tabla de datos del Ejercicio Guiado2.doc
Figura 27: Tabla de datos del Ejercicio Guiado2.doc
-
¿Se puede afirmar que los diferentes genotipos no influyen en el número de días hasta la aparición de la infección? ¿Se puede concluir que los distintos fotoperiodos no afectan al tiempo de aparición de los síntomas de infección del moho?
-
En caso de que influyan significativamente alguno de los dos factores, extraer conclusiones utilizando el método de Duncan.
-
Estudiar las hipótesis de modelo: Homocedasticidad, Independencia y Normalidad.
Ejercicio Guiado3
Se realiza un estudio para determinar el efecto del nivel del agua y del tipo de planta sobre la longitud global del tallo de las plantas de guisantes. Para ello, se utilizan tres niveles de agua (bajo, medio y alto) y dos tipos de plantas (sin hojas y convencional). Se dispone para el estudio de dieciocho plantas sin hojas y dieciocho plantas convencionales. Se dividen aleatoriamente los dos tipos de plantas en tres subgrupos y después se asignan los niveles de agua aleatoriamente a los dos grupos de plantas. Los datos sobre la longitud del tallo de los guisantes (en centímetros) se muestran en la siguiente tabla:
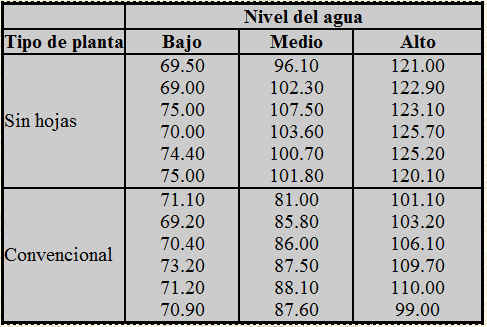 Figura 28: Tabla de datos del Ejercicio Guiado3.doc
Figura 28: Tabla de datos del Ejercicio Guiado3.doc
Para un nivel de significación del 5%.
-
¿Se puede afirmar que los distintos niveles de agua influyen en la longitud del tallo de los guisantes? ¿Y el tipo de planta?
-
¿La efectividad del nivel del agua es la misma para los dos tipos de plantas?
-
Estudia, utilizando el método de Newman-Keuls, qué nivel de agua es más efectivo.
Ejercicio Guiado 1 (Resuelto)
Se realiza un estudio del contenido de azufre en cinco yacimientos de carbón. Se toman muestras aleatoriamente de cada uno de los yacimientos y se analizan. Los datos del porcentaje de azufre por muestra se indican en la tabla adjunta.
 Figura 26: Tabla de datos del Ejercicio Guiado1.doc
Figura 26: Tabla de datos del Ejercicio Guiado1.doc
Para un nivel de significación del 5%.
- ¿Se puede confirmar que el porcentaje de azufre es el mismo en los cinco yacimientos?
- Si se rechaza la hipótesis nula que las medias de porcentaje de azufre en los cinco yacimientos es la misma, determinar que medias difieren entre sí utilizando el método de comparaciones múltiples de Tukey.
- Estudiar las hipótesis de modelo: Homocedasticidad (Homogeneidad de las varianzas por grupo), Independencia y Normalidad.
Solución:
- ¿Se puede confirmar que el porcentaje de azufre es el mismo en los cinco yacimientos?
El problema planteado se modeliza a través de un diseño unifactorial totalmente aleatorizado de efectos fijos no-equilibrado.
- Variable respuesta: Contenido de Azufre
- Factor: Tipo de yacimiento con cinco niveles. Es un factor de Efectos fijos ya que viene decidido qué niveles concretos se van a utilizar
- Modelo no-equilibrado: Los niveles de los factores tienen distinto número de elementos
- Tamaño del experimento: Número total de observaciones, en este caso 41 unidades experimentales.
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos realizarlo directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto:
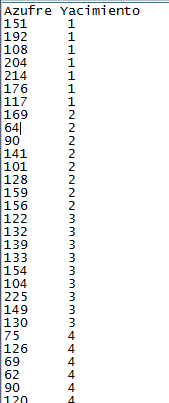
Figura 27: Tabla de datos del Ejercicio Guiado1.txt
En primer lugar describimos los cinco grupos que tenemos que comparar, los cinco yacimientos, la variable respuesta es el porcentaje de azufre en estos cinco yacimientos. Los yacimientos no tienen todos el mismo número de observaciones, en total tenemos 41 observaciones. La hipótesis nula es que el porcentaje de azufre es el mismo en los cinco yacimientos… Es decir, no hay diferencias en los porcentajes de azufre con respecto a los distintos yacimientos y la hipótesis alternativa es que el porcentaje de azufre es diferente al menos en dos yacimientos.
Tenemos en cuenta que para que el ejercicio esté realizado de forma correcta los datos tienen que estar introducidos tal y como vienen en Figura 27, es decir, las observaciones en una sola columna y a continuación especificado su tratamiento y su bloque correspondiente.
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
Nota: La ruta hasta llegar al fichero varía en función del ordenador. Utilizar la orden setwd() para situarse en el directorio de trabajo
> setwd(“C:/Users/Usuario/Desktop/Datos”)
> porcentaje <- read.table(“guiado1.txt”, header = TRUE)
> porcentaje
Azufre Yacimiento
1 151 1
2 192 1
3 108 1
4 204 1
5 214 1
6 176 1
7 117 1
8 169 2
9 64 2
10 90 2
11 141 2
12 101 2
13 128 2
14 159 2
15 156 2
16 122 3
17 132 3
18 139 3
19 133 3
20 154 3
21 104 3
22 225 3
23 149 3
24 130 3
25 75 4
26 126 4
27 69 4
28 62 4
29 90 4
30 120 4
31 32 4
32 73 4
33 80 5
34 90 5
35 124 5
36 82 5
37 72 5
38 57 5
39 118 5
40 54 5
41 130 5
Debemos transformar la variable referente a los niveles del factor fijo como factor para poder hacer los cálculos de forma adecuada:
> porcentaje$Yacimiento<-factor(porcentaje$Yacimiento)
> porcentaje$Yacimiento
[1] 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 5 5 5 5 5 5
[39] 5 5 5
Levels: 1 2 3 4 5
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma:
> mod <- aov(Azufre ~ Yacimiento, data = porcentaje)
donde:
- Azufre: Nombre de la columna de las observaciones.
- Yacimiento: Nombre de la columna en la que están representados los tratamientos.
- data= data.frame en el que están guardados los datos.
> mod
Call:
aov(formula = Azufre ~ Yacimiento, data = porcentaje)
Terms:
Yacimiento Residuals
Sum of Squares 40432.68 42639.76
Deg. of Freedom 4 36
Residual standard error: 34.41566
Estimated effects may be unbalanced
Se puede mostrar un resumen de los resultados con la función “summary” (verdadera tabla ANOVA)
> summary(mod)
Df Sum Sq Mean Sq F value Pr(>F)
Yacimiento 4 40433 10108 8.534 5.97e-05 ***
Residuals 36 42640 1184
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
En la Tabla ANOVA, el valor del estadístico de contraste de igualdad de medias, F = 8.534 deja a su derecha un p-valor menor que 0.001, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias. Es decir, existen diferencias significativas en el contenido medio de azufre entre los cinco yacimientos. La pregunta que nos planteamos es si el contenido de azufre es significativamente distinto en los cinco yacimientos o sólo en alguno de ellos. Para responder a esta pregunta utilizamos algún procedimiento de comparaciones múltiples. En el apartado siguiente responderemos a esta cuestión.
2. Si se rechaza la hipótesis nula que las medias de porcentaje de azufre en los cinco yacimientos es la misma, determinar que medias difieren entre sí utilizando el método de comparaciones múltiples de Tukey.
> mod.tukey <- TukeyHSD(mod, ordered = TRUE)
> mod.tukey
Tukey multiple comparisons of means
95% family-wise confidence level
factor levels have been ordered
Fit: aov(formula = Azufre ~ Yacimiento, data = porcentaje)
$Yacimiento
diff lwr upr p adj
5-4 8.791667 -39.217257 56.80059 0.9841364
2-4 45.125000 -4.275775 94.52577 0.0873389
3-4 62.236111 14.227188 110.24503 0.0057086
1-4 85.125000 33.990340 136.25966 0.0002709
2-5 36.333333 -11.675590 84.34226 0.2131394
3-5 53.444444 6.868947 100.01994 0.0177365
1-5 76.333333 26.542032 126.12463 0.0008288
3-2 17.111111 -30.897812 65.12003 0.8429902
1-2 40.000000 -11.134660 91.13466 0.1865081
1-3 22.888889 -26.902412 72.68019 0.6809794
Se comprueba que no se detectan diferencias significativas entre los yacimientos 1, 2 y 3 y entre los yacimientos 2, 4 y 5. Para ello nos fijamos en las Significaciones (mayores que 0.05) o en los límites de los intervalos. Dos medias se declaran iguales si el cero pertenece al intervalo de confianza construido para la diferencia de ellas.
3. Estudiar las hipótesis de modelo: Homocedasticidad (Homogeneidad de las varianzas por grupo), Independencia y Normalidad.
Hipótesis de Homocedasticidad: Test de Barlett
> bartlett.test(porcentaje$Azufre, porcentaje$Yacimiento)
Bartlett test of homogeneity of variances
data: porcentaje$Azufre and porcentaje$Yacimiento
Bartlett’s K-squared = 1.2655, df = 4, p-value = 0.8672
La salida muestra el resultado del contraste de Barlett de igualdad de varianzas en todos los grupos. El estadístico de contraste experimental, B= 1.2655, deja a la derecha un p-valor = 0.8672, que nos indica que no se debe rechazar la igualdad entre las varianzas.
Hipótesis de Independencia: Esta hipótesis la comprobaremos gráficamente mediante la representación de los residuos frente a los valores pronosticados por el modelo.
> layout(matrix(c(1,2,3,4),2,2))
> plot(mod)
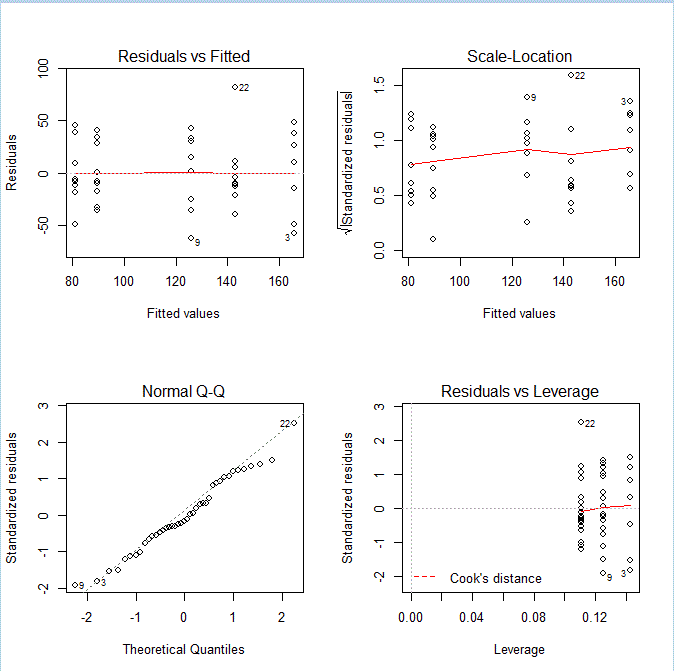
Figura 28: Gráficos para comprobar la hipóetsis de independencia
En esta salida interpretamos el gráfico que se muestra en la Fila 1, Columna 1. Es decir, el gráfico el que se representan los residuos en el eje de ordenadas y los valores ajustados por el modelo en el eje de abscisas. Este gráfico no muestra ningún aspecto que haga sospechar de la hipótesis de independencia de los residuos.
La hipótesis de Normalidad la comprobaremos gráficamente y analíticamente
Gráficamente comprobaremos la normalidad mediante un histograma y el gráfico Q-Q plot
En primer lugar realizaremos el histograma, para ello
En primer lugar calculemos los residuos del modelo
> g = mod$residuals
> g
1 2 3 4 5 6
-15.0000000 26.0000000 -58.0000000 38.0000000 48.0000000 10.0000000
7 8 9 10 11 12
-49.0000000 43.0000000 -62.0000000 -36.0000000 15.0000000 -25.0000000
13 14 15 16 17 18
2.0000000 33.0000000 30.0000000 -21.1111111 -11.1111111 -4.1111111
19 20 21 22 23 24
-10.1111111 10.8888889 -39.1111111 81.8888889 5.8888889 -13.1111111
25 26 27 28 29 30
-5.8750000 45.1250000 -11.8750000 -18.8750000 9.1250000 39.1250000
31 32 33 34 35 36
-48.8750000 -7.8750000 -9.6666667 0.3333333 34.3333333 -7.6666667
37 38 39 40 41
-17.6666667 -32.6666667 28.3333333 -35.6666667 40.3333333
Calculamos la media de los residuos
> m <- mean(g)
> m
[1] -3.462677e-16
Calculamos la desviación típica
> std <- sqrt(var(g))
> std
[1] 32.64957
Representamos el histograma
> hist(g, prob = TRUE, xlab =”Residuos”, ylim = c(0, 0.025), main = “F. dens. Normal hist. de residuos”)
Y la curma Normal sobre el Histograma
> curve(dnorm(x, mean = m, sd = std), col =”darkblue”, lwd =2, add = TRUE, yaxt =”n”)
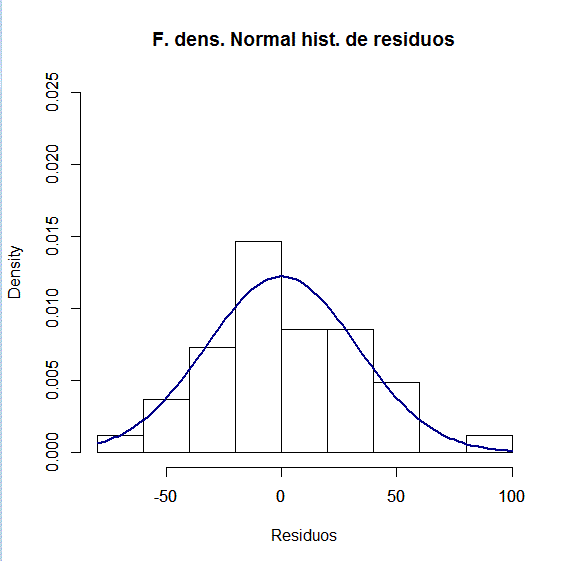 Figura 29: Histograma con curva Normal
Figura 29: Histograma con curva Normal
Anteriormete hemos realizado el gráfico Q-Q. Ambos gráficos no muestran desviación importante de la normalidad.
Analíticamente lo vamos a comprobar mediante el contraste de Shapiro-Wilk
> shapiro.test(mod$residuals)
Shapiro-Wilk normality test
data: mod$residuals
W = 0.97902, p-value = 0.6384
El valor del p-valor (Sig. asintót. (bilateral)) es de 0.6384, por lo tanto no podemos rechazar la hipótesis de normalidad.
Ejercicio Guiado 2 (Resuelto)
Se realiza un estudio sobre el efecto del fotoperiodo y del genotipo en el periodo latente de infección del moho de cebada aislado AB3. Se obtienen cincuenta hojas de cuatro genotipos distintos. Cada grupo es infectado y posteriormente expuesto a diferente fotoperiodo. Los distintos fotoperiodos se trataron como bloques y se obtuvieron los siguientes datos de los totales para los bloques y tratamientos. La respuesta anotada es el número de días hasta la aparición de síntomas visibles.
 Figura 30: Tabla de datos del Ejercicio Guiado2.doc
Figura 30: Tabla de datos del Ejercicio Guiado2.doc
-
¿Se puede afirmar que los diferentes genotipos no influyen en el número de días hasta la aparición de la infección? ¿Se puede concluir que los distintos fotoperiodos no afectan al tiempo de aparición de los síntomas de infección del moho?
-
En caso de que influyan significativamente alguno de los dos factores, extraer conclusiones utilizando el método de Duncan.
-
Estudiar las hipótesis de modelo: Homocedasticidad, Independencia y Normalidad.
Solución:
- ¿Se puede afirmar que los diferentes genotipos no influyen en el número de días hasta la aparición de la infección? ¿Se puede concluir que los distintos fotoperiodos no afectan al tiempo de aparición de los síntomas de infección del moho?
En este caso se trata de un diseño en bloques completos aleatorizados. El objetivo del estudio es comparar los cuatro tipos de genotipos, por lo que se trata de un factor con cuatro niveles. Sin embargo, al realizar la medición con los distintos fotoperiodos a los que son expuestos el moho de cebada, es posible que estos influyan sobre el periodo latente de infección del moho de cebada aislado AB3. Por ello, y al no ser directamente motivo de estudio, los fotoperiodos es un factor secundario que recibe el nombre de bloque.
Este modelo tiene que verificar los siguientes supuestos:
- Las 20 observaciones constituyen muestras aleatorias independientes, cada una de tamaño 3, de 20 poblaciones con medias μij, i=1, 2, 3, 4 y j = 1, 2, 3, 4,5.
- Cada una de las 20 poblaciones es normal.
- Cada una de las 20 poblaciones tiene la misma varianza.
- Los efectos de los bloques y tratamientos son aditivos; es decir, no existe interacción entre los bloques y tratamientos. Esto significa que si hay diferencias entre dos tratamientos cualesquiera, estas se mantienen en todos los bloques (abetos).
Los tres primeros supuestos coinciden con los supuestos del modelo unifactorial, con la diferencia de que en el modelo unifactorial se examinaban I poblaciones y en este modelo se examinan IJ. El cuarto supuesto es característico del diseño en bloques. La no interacción entre los bloques y los tratamientos significa que los tratamientos tienen un comportamiento consistente a través de los bloques y que los bloques tienen un comportamiento consistente a través de los tratamientos. Expresado matemáticamente significa que la diferencia de los valores medios para dos tratamientos cualesquiera es la misma en todo un bloque y que la diferencia de los valores medios para dos bloques cualesquiera es la misma para cada tratamiento.
- Variable respuesta: Número de días hasta la aparición de síntomas visibles
- Factor: Genotipo que tiene cuatro niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Bloque: Fotoperiodo que tiene cinco niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Modelo completo: Los cuatro tratamientos se prueban en cada bloque exactamente una vez.
- Tamaño del experimento: Número total de observaciones (20).
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto:
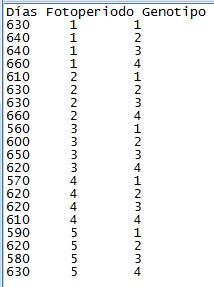
Figura 31: Tabla de datos del Ejercicio Guiado2.txt
Primero nos situaremos en el directorio de trabajo
> setwd (“C:/Users/Usuario/Desktop/Datos”)
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
> dias<-read.table(“guiado2.txt”, header = TRUE)
> dias
Días Fotoperiodo Genotipo
1 630 1 1
2 640 1 2
3 640 1 3
4 660 1 4
5 610 2 1
6 630 2 2
7 630 2 3
8 660 2 4
9 560 3 1
10 600 3 2
11 650 3 3
12 620 3 4
13 570 4 1
14 620 4 2
15 620 4 3
16 610 4 4
17 590 5 1
18 620 5 2
19 580 5 3
20 630 5 4
A continuación debemos transformar tanto la columna de los tratamientos como la de los bloques en un factor para realizar los cálculos posteriores adecuadamente.
> dias$Fotoperiodo = factor(dias$Fotoperiodo)
> dias$Fotoperiodo
[1] 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5
Levels: 1 2 3 4 5
> dias$Genotipo = factor(dias$Genotipo)
> dias$Genotipo
[1] 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
Levels: 1 2 3 4
Para calcular la tabla ANOVA primero hacemos uso de la función “aov” de la siguiente forma
> mod = aov(Días ~ Fotoperiodo + Genotipo, data = dias)
donde:
- Días: Nombre de la columna de las observaciones
- Fotoperiodo: Nombre de la columna en la que están representados los tratamientos
- Genotipo: Nombre de la columna en la que están representados los bloques
- data = data.frame en el que están guardados los datos
Ejecutamos
> mod
Call:
aov(formula = Días ~ Fotoperiodo + Genotipo, data = dias)
Terms:
Fotoperiodo Genotipo Residuals
Sum of Squares 5030 5255 4170
Deg. of Freedom 4 3 12
Residual standard error: 18.64135
Estimated effects may be unbalanced
y a continuacion mostramos un resumen de los resultados con la función “summary” (verdadera tabla ANOVA):
> summary(mod)
Df Sum Sq Mean Sq F value Pr(>F)
Fotoperiodo 4 5030 1257.5 3.619 0.0371 *
Genotipo 3 5255 1751.7 5.041 0.0173 *
Residuals 12 4170 347.5
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
En la Tabla ANOVA, el valor del estadístico de contraste de igualdad de medias de tratamientos, F = 5.041 deja a su derecha un p-valor igual a 0.017, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias de tratamientos. Es decir, existen diferencias significativas en el número de días hasta la aparición de la infección entre los cuatro genotipos.
En esta Tabla ANOVA, también se observa que el valor del estadístico de contraste de igualdad de medias de bloques, F = 3.619 deja a su derecha un p-valor igual a 0.037, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias de bloques. Es decir, existen diferencias significativas en el número de días hasta la aparición de la infección entre los cinco tipos de fotoperiodos. Por lo tanto, se concluye que los niveles de ambos factores influyen de forma significativa en el número de días hasta la aparición de los síntomas de infección del moho.
2. En caso de que influyan significativamente alguno de los dos factores, extraer conclusiones utilizando el método de Duncan.
Primero vamos a hacer el contraste de Duncan para los tratamientos: Genotipos
> duncan <-duncan.test(mod, “Genotipo” , main= ” Número de días con diferentes genotipos “)
> duncan
$statistics
MSerror Df Mean CV
347.5 12 618.5 3.013962
$parameters
test name.t ntr alpha
Duncan Genotipo 4 0.05
$duncan
Table CriticalRange
2 3.081307 25.68782
3 3.225244 26.88778
4 3.312453 27.61481
$means
Días std r Min Max Q25 Q50 Q75
1 592 28.63564 5 560 630 570 590 610
2 622 14.83240 5 600 640 620 620 630
3 624 27.01851 5 580 650 620 630 640
4 636 23.02173 5 610 660 620 630 660
$comparison
NULL
$groups
Días groups
4 636 a
3 624 a
2 622 a
1 592 b
attr(,”class”)
[1] “group”
En la tabla del factor Tipo de genotipo hay dos subconjuntos que se diferencian entre sí; el subconjunto 1 está formado por las medias del genotipo Armelle y el subconjunto 2 por las medias de los genotipos Golden, Promise y Emir. Y dentro de cada subconjunto no se aprecian diferencias significativas entre las medias. También se observa que en el genotipo Emir se produce el mayor número medio de días hasta la aparición de la infección (636) y en el genotipo Armelle se produce el menor (592).
Segundo vamos a hacer el contraste de Duncan para los bloques: Fotoperiodos
> duncan1 <-duncan.test(mod, “Fotoperiodo”, main= ” Número de días con diferentes fotoperiodos”)
> duncan1
$statistics
MSerror Df Mean CV
347.5 12 618.5 3.013962
$parameters
test name.t ntr alpha
Duncan Fotoperiodo 5 0.05
$duncan
Table CriticalRange
2 3.081307 28.71986
3 3.225244 30.06145
4 3.312453 30.87430
5 3.370172 31.41228
$means
Días std r Min Max Q25 Q50 Q75
1 642.5 12.58306 4 630 660 637.5 640 645.0
2 632.5 20.61553 4 610 660 625.0 630 637.5
3 607.5 37.74917 4 560 650 590.0 610 627.5
4 605.0 23.80476 4 570 620 600.0 615 620.0
5 605.0 23.80476 4 580 630 587.5 605 622.5
$comparison
NULL
$groups
Días groups
1 642.5 a
2 632.5 ab
3 607.5 b
4 605.0 b
5 605.0 b
attr(,”class”)
[1] “group”
En la tabla del factor Tipo de fotoperiodo hay dos subconjuntos que se diferencian entre sí; el subconjunto 1 está formado por las medias de los Fotoperiodos 0 y 2 y el subconjunto 2 por las medias de los fotoperiodos 2, 4, 8 y 16. Y dentro de cada subconjunto no se aprecian diferencias significativas entre las medias. También se observa que en el fotoperiodo 0 se produce el mayor número medio de días hasta la aparición de la infección (642.5) y en los fotoperiodos 8 y 16 se produce el menor
3. Estudiar las hipótesis de modelo: Homocedasticidad, Independencia y Normalidad.
Estudiamos la homocedasticidad mediante el test de Barlett
> bartlett.test(dias$Días, dias$Fotoperiodo)
Bartlett test of homogeneity of variances
data: dias$Días and dias$Fotoperiodo
Bartlett’s K-squared = 3.0629, df = 4, p-value = 0.5474
> bartlett.test(dias$Días, dias$Genotipo)
Bartlett test of homogeneity of variances
data: dias$Días and dias$Genotipo
Bartlett’s K-squared = 1.6252, df = 3, p-value = 0.6537
Las Tablas muestran los resultados del contraste de Barlett de igualdad de varianzas en todos los grupos del factor genotipo y en todos los grupos del factor Fotoperiodo. Los P-valores, 0.5474 y 0.6537 indican que indican que no se debe rechazar la igualdad entre las varianzas ni el factor genotipo ni el factor fotoperiodo.
Estudiamos la independencia gráficamente
> layout(matrix(c(1,2,3,4),2,2))
> plot(mod)
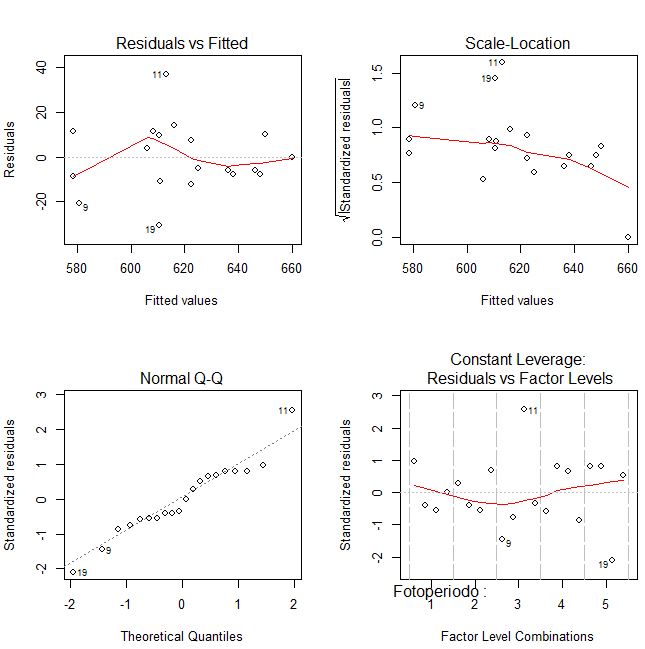
Figura 32: Diversos gráficos de los residuos
En esta salida, como en la figura 28, interpretamos el gráfico que se muestra en la Fila 1, Columna 1. Es decir, el gráfico el que se representan los residuos en el eje de ordenadas y los valores predichos por el modelo en el eje de abscisas. Este gráfico no muestra ningún aspecto que haga sospechar de la hipótesis de independencia de los residuos.
Estudiamos la Normalidad gráficamente mediante el gráfico probabilístico normal y analíticamente mediante el contraste de Shapiro-Wilk
Observamos el gráfico que se muestra en la Fila 2, Columna1. Es decir, el gráfico el que se representan los residuos estandarizados en el eje de ordenadas y cuantiles teóricos en el eje de abscisas. En dicho gráfico se aprecian desviaciones a la normalidad, pero el contraste ANOVA es robusto frente a desviaciones pequeñas de la normalidad. Realizaremos a continuación el contraste de Shapiro-Wilk para comprobar analíticamente la normalidad de los residuos.
> shapiro.test(mod$residuals)
Shapiro-Wilk normality test
data: mod$residuals
W = 0.95316, p-value = 0.4176
El valor del p-valor es de 0.4176, no pudiéndose rechazar la hipótesis de normalidad.
Ejercicio Guiado 3 (Resuelto)
Se realiza un estudio para determinar el efecto del nivel del agua y del tipo de planta sobre la longitud global del tallo de las plantas de guisantes. Para ello, se utilizan tres niveles de agua (bajo, medio y alto) y dos tipos de plantas (sin hojas y convencional). Se dispone para el estudio de dieciocho plantas sin hojas y dieciocho plantas convencionales. Se dividen aleatoriamente los dos tipos de plantas en tres subgrupos y después se asignan los niveles de agua aleatoriamente a los dos grupos de plantas. Los datos sobre la longitud del tallo de los guisantes (en centímetros) se muestran en la siguiente tabla:
 Figura 33: Tabla de datos del Ejercicio Guiado3.doc
Figura 33: Tabla de datos del Ejercicio Guiado3.doc
Para un nivel de significación del 5%.
-
¿Se puede afirmar que los distintos niveles de agua influyen en la longitud del tallo de los guisantes? ¿Y el tipo de planta?
-
¿La efectividad del nivel del agua es la misma para los dos tipos de plantas?
-
Estudia, utilizando el método de Newman-Keuls, qué nivel de agua es más efectivo.
Solución:
- ¿Se puede afirmar que los distintos niveles de agua influyen en la longitud del tallo de los guisantes? ¿Y el tipo de planta?
El problema planteado se modeliza a través de un ‘diseño de dos factores con replicación.
El modelo matemático es:
Yij= μ + τi + βj + (τβ)ij + uij, i=1,2,3; j=1,2
- Variable respuesta: Longitud del tallo
- Factor A: Nivel del agua con tres niveles. Es un factor de Efectos fijos.
- Factor B: Tipo de planta con dos niveles. Es un factor de Efectos fijos.
- Tamaño del experimento: Número total de observaciones (36).
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto:
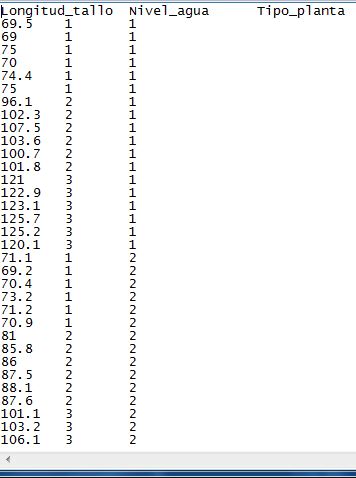
Figura 34: Tabla de datos del Ejercicio Guiado3.txt
Primero nos situaremos en el directorio de trabajo
> setwd (“C:/Users/Usuario/Desktop/Datos”)
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
> factorial<-read.table(“guiado3.txt”, header = TRUE)
>factorial
Longitud_tallo Nivel_agua Tipo_planta
1 69.5 1 1
2 69.0 1 1
3 75.0 1 1
4 70.0 1 1
5 74.4 1 1
6 75.0 1 1
7 96.1 2 1
8 102.3 2 1
9 107.5 2 1
10 103.6 2 1
11 100.7 2 1
12 101.8 2 1
13 121.0 3 1
14 122.9 3 1
15 123.1 3 1
16 125.7 3 1
17 125.2 3 1
18 120.1 3 1
19 71.1 1 2
20 69.2 1 2
21 70.4 1 2
22 73.2 1 2
23 71.2 1 2
24 70.9 1 2
25 81.0 2 2
26 85.8 2 2
27 86.0 2 2
28 87.5 2 2
29 88.1 2 2
30 87.6 2 2
31 101.1 3 2
32 103.2 3 2
33 106.1 3 2
34 109.7 3 2
35 110.0 3 2
36 99.0 3 2
A continuación debemos transformar todas las columnas que contienen a los factores en un factor para poder realizar los cálculos posteriores adecuadamente.
> factorial$agua <- factor(factorial$Nivel_agua)
> factorial$agua
[1] 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3
Levels: 1 2 3
> factorial$planta <- factor(factorial$Tipo_planta)
> factorial$planta
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
Levels: 1 2
Para responder a este apartado debe resolverse el contraste de igualdad de medias para el factor A:
H0= μ1= μ2= μ3= μ vs H1= μi ≠ μj para algún i≠ j
y para el factor B:
H0= μ1= μ2= μ vs H1= μi ≠ μj para algún i≠ j
Para calcular la tabla ANOVA en R primero hacemos uso de la función “aov” y a continuación “summary” de la siguiente forma:
> mod = aov(Longitud_tallo ~ agua* planta , data = factorial )
> mod
Call:
aov(formula = Longitud_tallo ~ agua * planta, data = factorial)
Terms:
agua planta agua:planta Residuals
Sum of Squares 10773.635 1246.090 514.145 282.250
Deg. of Freedom 2 1 2 30
Residual standard error: 3.067301
Estimated effects may be unbalanced
> summary(mod)
Df Sum Sq Mean Sq F value Pr(>F)
agua 2 10774 5387 572.56 < 2e-16 ***
planta 1 1246 1246 132.44 1.58e-12 ***
agua:planta 2 514 257 27.32 1.75e-07 ***
Residuals 30 282 9
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
- El valor del estadístico de contraste de igualdad de medias del factor Nivel_agua, F= 572.56 deja a su derecha un p-valor menor que 0.001, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias de los niveles del factor Nivel_agua. Es decir, existen diferencias significativas en la longitud del tallo de guisantes dependiendo del nivel del agua.
- El valor del estadístico de contraste de igualdad de medias del factor Tipo_planta, F= 132.445 deja a su derecha un p-valor menor que 0.001, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de medias del factor Tipo_planta. Es decir, el tipo de planta afecta significativamente a la longitud del tallo de guisantes.
2. ¿La efectividad del nivel del agua es la misma para los dos tipos de plantas?
Para responder a esta pregunta, realizamos el contraste de hipótesis sobre la interacción de los dos factores
H0 = (τβ)ij = 0 (no existe interacción) vs H1 = (τβ)ij ≠ 0 (existe interacción).
En la Tabla ANOVA mostrada anteriormente, el valor del estadístico de contraste de la interacción de los dos factores, F= 27.32 deja a su derecha un p-valor menor que 0.001, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de no interacción entre los factores. Por lo tanto la efectividad del nivel de agua no es la misma para los dos tipos de plantas. Es decir, puede ocurrir que un nivel de agua influya en el crecimiento de la longitud del tallo con un tipo de planta pero no con el otro o influya de distinta forma.
3. Estudia, utilizando el método de Newman- Keuls, qué nivel de agua es más efectivo.
> library(agricolae)
Warning message:
replacing previous import ‘Matrix::expm’ by ‘expm::expm’ when loading ‘spdep’
> contraste <- SNK.test(mod,”agua”, console=TRUE, main=” Contraste de Newman-Keuls para el factor nivel del agua”)
Study: Contraste de Newman-Keuls para el factor nivel del agua
Student Newman Keuls Test
for Longitud_tallo
Mean Square Error: 9.408333
agua, means
Longitud_tallo std r Min Max
1 71.575 2.243019 12 69 75.0
2 94.000 8.901992 12 81 107.5
3 113.925 10.069949 12 99 125.7
Alpha: 0.05 ; DF Error: 30
Critical Range
2 3
2.557375 3.087063
Means with the same letter are not significantly different.
Longitud_tallo groups
3 113.925 a
2 94.000 b
1 71.575 c
En la tabla se muestran los subgrupos formados de medias iguales al utilizar el método de Newman-Keuls. Hay tres subconjuntos que se diferencian entre sí y cada subconjunto está formado por un solo nivel de agua. También se observa que con el nivel de agua alto se produce la mayor longitud del tallo de guisantes, 113.925 cm, y con el nivel Bajo se produce el menor 71.575 cm.
Ejercicios Propuestos
Ejercicio Propuesto 1
La convección es una forma de transferencia de calor por los fluidos debido a sus variaciones de densidad por la temperatura; las partes calientes ascienden y las frías descienden formando las corrientes de convección que hacen uniforme la temperatura del fluido. Se ha realizado un experimento para determinar las modificaciones de la densidad de fluido al elevar la temperatura en una determinada zona. Los resultados obtenidos han sido los siguientes:
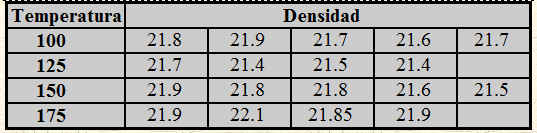 Figura 34: Tabla de datos del Ejercicio Propuesto1.doc
Figura 34: Tabla de datos del Ejercicio Propuesto1.doc
Responder a las siguientes cuestiones:
- ¿Afecta la temperatura a la densidad del fluido?
-
Determinar qué temperaturas producen modificaciones significativas en la densidad media del fluido.
- Estudiar las hipótesis del modelo: Homocedasticidad, independencia y normalidad.
-
¿Se puede afirmar que las temperaturas de 100 y 125 producen menos densidades de fluido en promedio que las temperaturas de 150 y 175?
Ejercicio Propuesto 2
Un laboratorio de reciclaje controla la calidad de los plásticos utilizados en bolsas. Se desea contrastar si existe variabilidad en la calidad de los plásticos que hay en el mercado. Para ello, se eligen al azar cuatro plásticos y se les somete a una prueba para medir el grado de resistencia a la degradación ambiental. De cada plástico elegido se han seleccionado ocho muestras y los resultados de la variable que mide la resistencia son los de la tabla adjunta.
 Figura 35: Tabla de datos del Ejercicio Propuesto2.doc
Figura 35: Tabla de datos del Ejercicio Propuesto2.doc
¿Qué conclusiones se deducen de este experimento?
Ejercicio Propuesto 3
Debido a la proliferación de los campos de golf y a la gran cantidad de agua que necesitan, un grupo de científicos estudia la calidad de varios tipos de césped para implantarlo en invierno en los campos de golf. Para ello, miden la distancia recorrida por una pelota de golf, en el campo, después de bajar por una rampa (para proporcionar a la pelota una velocidad inicial constante). El terreno del que disponen tiene mayor pendiente en la dirección norte-sur, por lo que se aconseja dividir el terreno en cinco bloques de manera que las pendientes de las parcelas individuales dentro de cada bloque sean las mismas. Se utilizó el mismo método para la siembra y las mismas cantidades de semilla. Las mediciones son las distancias desde la base de la rampa al punto donde se pararon las pelotas. En el estudio se incluyeron las variedades: Agrostis Tenuis (Césped muy fino y denso, de hojas cortas y larga duración), Agrostis Canina (Hoja muy fina, estolonífera. Forma una cubierta muy tupida), Paspalum Notatum (Hojas gruesas, bastas y con rizomas. Forma una cubierta poco densa), Paspalum Vaginatum (Césped fino, perenne, con rizomas y estolones).
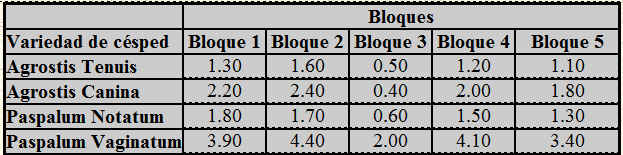 Figura 35: Tabla de datos del Ejercicio Propuesto 3.doc
Figura 35: Tabla de datos del Ejercicio Propuesto 3.doc
Se pide:
-
Identificar los elementos del estudio (factores, unidades experimentales, variable respuesta, etc.) y plantear detalladamente el modelo matemático utilizado en el experimento.
- ¿Son los bloques fuente de variación?
- Existen diferencias reales entre las distancias medias recorridas por una pelota de golf en los distintos tipos de césped?
- Estudiar las interacciones de los factores.
- Comprobar que se cumplen las hipótesis del modelo.
-
Utilizando el método de Duncan y Newman-Keuls, ¿qué tipo de césped ofrece menor resistencia al recorrido de las pelotas?
Ejercicio Propuesto 4
Consideremos de nuevo el ejercicio propuesto 3 sobre un grupo de científicos que estudia la calidad de varios tipos de césped para implantarlo en invierno en los campos de golf. Para ello, miden la distancia recorrida por una pelota de golf, en el campo, después de bajar por una rampa (para proporcionar a la pelota una velocidad inicial constante). El terreno del que disponen tiene mayor pendiente en la dirección norte-sur, por lo que se aconseja dividir el terreno en seis bloques de manera que las pendientes de las parcelas individuales dentro de cada bloque sean las mismas. Se utilizó el mismo método para la siembra y las mismas cantidades de semilla. Las mediciones son las distancias desde la base de la rampa al punto donde se pararon las pelotas, y al realizar dichas mediciones no se han podido obtener una para cada combinación de tipo de césped y tipo de terreno, sino que sólo se han podido realizar con tres de las variedades del césped en cada uno de los bloques de terreno. Para controlar el efecto del tipo de terreno deciden utilizar un diseño en bloques incompletos. En el estudio se incluyeron las variedades: Agrostis Tenuis (Césped muy fino y denso, de hojas cortas y larga duración), Agrostis Canina (Hoja muy fina, estolonífera. Forma una cubierta muy tupida), Paspalum Notatum (Hojas gruesas, bastas y con rizomas. Forma una cubierta poco densa), Paspalum Vaginatum (Césped fino, perenne, con rizomas y estolones).
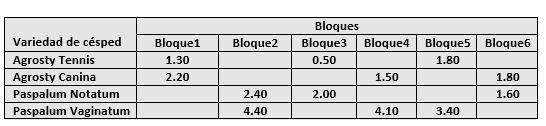
Figura 36: Tabla de datos del Ejercicio Propuesto 4.doc
Se pide:
-
Identificar los elementos del estudio (factores, unidades experimentales, variable respuesta, etc.) y plantear detalladamente el modelo matemático utilizado en el experimento.
- ¿Son los bloques fuente de variación?
- Existen diferencias reales entre las distancias medias recorridas por una pelota de golf en los distintos tipos de césped?
- Comprobar que se cumplen las hipótesis del modelo.
-
Utilizando el método de Newman-Keuls, ¿qué tipo de césped ofrece menor resistencia al recorrido de las pelotas?
Ejercicio Propuesto 5
Un investigador quiere evaluar la productividad de cuatro variedades de aguacates, A, B, C y D. Para ello decide realizar el ensayo en un terreno que posee un gradiente de pendiente de oriente a occidente y además, diferencias en la disponibilidad de Nitrógeno de norte a sur, para controlar los efectos de la pendiente y la disponibilidad de Nitrógeno, utilizó un diseño de cuadrado latino, los datos corresponden a la producción en kg/parcela.
 Figura 37: Tabla de datos del Ejercicio Propuesto 5.doc
Figura 37: Tabla de datos del Ejercicio Propuesto 5.doc
Responder a las siguientes cuestiones:
-
¿Se puede afirmar que la productividad media de las cuatro variedades de aguacate es la misma?
-
¿Qué supuestos han de verificarse?
- ¿Se obtiene la misma producción con las cuatro variedades de aguacate? En caso negativo, analizar mediante el procedimiento de Tukey y Newman-Keuls, con qué variedad de aguacate hay mayor producción.
Ejercicio Propuesto 6
Consideremos de nuevo el ejercicio propuesto 5 del investigador que quiere evaluar la productividad de cuatro variedades de aguacate, A, B, C y D. Para ello, decide realizar el ensayo en un terreno que posee un gradiente de pendiente de oriente a occidente y además, diferencias en la disponibilidad de Nitrógeno de norte a sur. Se seleccionan cuatro disponibilidades de nitrógeno, pero sólo dispone de tres gradientes de pendiente. Para controlar estas posibles fuentes de variabilidad, el investigador decide utilizar un diseño en cuadrado de Youden con cuatro filas, las cuatro disponibilidades de Nitrógeno (NI, N2, N3, N4), tres columnas, los tres gradientes de pendientes (P1, P2, P3) y cuatro letras latinas, las variedades de aguacates (A, B, C, D). Los datos corresponden a la producción en kg/parcela.
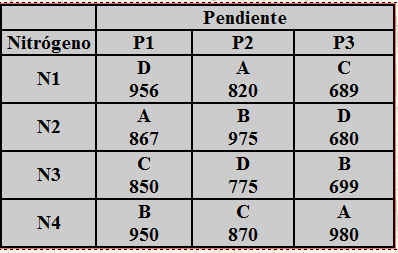 Figura 38: Tabla de datos del Ejercicio Propuesto 6.doc
Figura 38: Tabla de datos del Ejercicio Propuesto 6.doc
Responder a las siguientes cuestiones:
-
Estudiar cuál es el tipo de diseño adecuado a este experimento y escribir el modelo matemático asociado.
- ¿Se puede afirmar que la productividad media de las cuatro variedades de aguacate es la misma?
- Comprobar la hipótesis de homocedasticidad
- ¿Se obtiene la misma producción con las cuatro variedades de aguacate? En caso negativo, analizar mediante el procedimiento de Duncan, con qué variedad de aguacate hay mayor producción.
Ejercicio Propuesto 7
En un invernadero se está estudiando el crecimiento de determinadas plantas, para ello se quiere controlar los efectos del terreno, abono, insecticida y semilla. El estudio se realiza con cuatro tipos de semillas diferentes que se plantan en cuatro tipos de terreno, se les aplican cuatro tipos de abonos y cuatro tipos de insecticidas. La asignación de los tratamientos a las plantas se realiza de forma aleatoria. Para controlar estas posibles fuentes de variabilidad se decide plantear un diseño por cuadrados greco-latinos como el que se muestra en la siguiente tabla, donde las letras griegas corresponden a los cuatro tipos de semilla y las latinas a los abonos.
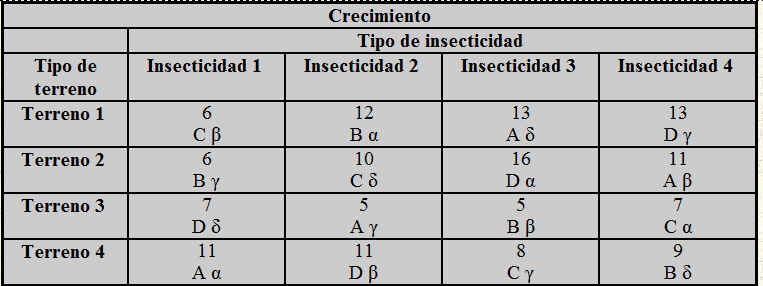 Figura 39: Tabla de datos del Ejercicio Propuesto 7.doc
Figura 39: Tabla de datos del Ejercicio Propuesto 7.doc
Responder a las siguientes cuestiones:
-
Estudiar cuál es el tipo de diseño adecuado a este experimento y escribir el modelo matemático asociado.
-
¿Se puede afirmar que el crecimiento de las plantas es el mismo para los cuatro tipos de abonos? ¿Y con los distintos insecticidas?
-
¿Existen diferencias significativas en el crecimiento de las plantas con las distintas semillas? ¿Y el tipo de tierra influye en dicho crecimiento?
-
¿Con qué tipo de semilla se produce el mayor crecimiento de las plantas?
- ¿El crecimiento de las plantas es el mismo utilizando al mismo tiempo los abonos A y B que utilizando los abonos C y D?
Ejercicio Propuesto 8
Se realiza un estudio sobre el efecto que produce la descarga de aguas residuales de una planta sobre la ecología del agua natural de un río. En el estudio se utilizaron dos lugares de muestreo. Un lugar está aguas arriba del punto en el que la planta introduce aguas residuales en la corriente; el otro está aguas abajo. Se tomaron muestras durante un periodo de cuatro semanas y se obtuvieron los datos sobre el número de diatomeas halladas. Los datos se muestran en la tabla adjunta:
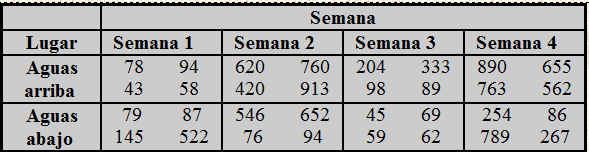 Figura 40: Tabla de datos del Ejercicio Propuesto 8.doc
Figura 40: Tabla de datos del Ejercicio Propuesto 8.doc
Responder a las siguientes cuestiones:
-
Identificar el diseño adecuado a este experimento, escribir el modelo matemático y explicar los distintos elementos que intervienen.
-
Estudiar si la semana y el lugar son factores determinantes en el número de diatomeas halladas en el agua del río. ¿Hay posibilidad que una semana sea más recomendable en un lugar del río en concreto y no lo sea en el otro lugar?
-
Estudiar en qué semana se producen menos contaminación en el río, utilizando el método de Duncan.
-
Estudiar en qué lugar del río se producen menos diatomeas.
Ejercicio Propuesto 9
La cotinina es uno de los principales metabolitos de la nicotina. Actualmente se le considera el mejor indicador de la exposición al humo de tabaco. Se ha realizado un estudio con distintas marcas de tabaco distinguiendo principalmente entre negro y rubio para detectar las posibles diferencias en el nivel de nicotina de personas expuestas al humo de tabaco. Para ello, se han analizado personas de distintas edades (niños, jóvenes y adultos) y se ha distinguido entre mujeres y hombres. Se han obtenido los datos de la siguiente tabla sobre el nivel de nicotina en miligramos por mililitro.
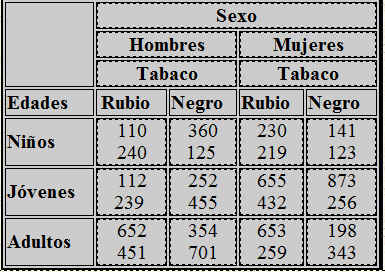 Responder a las siguientes cuestiones:
Responder a las siguientes cuestiones:
-
Identificar el diseño adecuado a este experimento, escribir el modelo matemático y explicar los distintos elementos que intervienen.
-
Contrastar la hipótesis nula de no interacción entre los factores. Adecuar el modelo al resultado de las interacciones y contrastar los efectos principales.
-
¿Hay diferencias significativas en el nivel de nicotina en las distintas edades? ¿En qué edad el nivel de nicotina es mayor?
- ¿El tipo de tabaco es un factor determinante en el nivel de nicotina?
-
Comparar el nivel medio de nicotina entre las mujeres y los hombres. ¿Se detectan diferencias significativas?
Ejercicio Propuesto 1 (Resuelto)
La convección es una forma de transferencia de calor por los fluidos debido a sus variaciones de densidad por la temperatura; las partes calientes ascienden y las frías descienden formando las corrientes de convección que hacen uniforme la temperatura del fluido. Se ha realizado un experimento para determinar las modificaciones de la densidad de fluido al elevar la temperatura en una determinada zona. Los resultados obtenidos han sido los siguientes:
 Figura 34: Tabla de datos del Ejercicio Propuesto1.doc
Figura 34: Tabla de datos del Ejercicio Propuesto1.doc
Responder a las siguientes cuestiones:
- ¿Afecta la temperatura a la densidad del fluido?
-
Determinar qué temperaturas producen modificaciones significativas en la densidad media del fluido.
- Estudiar las hipótesis del modelo: Homocedasticidad, independencia y normalidad.
-
Se puede afirmar que las temperaturas de 100 y 125 producen menos densidades de fluido en promedio que las temperaturas de 150 y 175.
Solución:
El problema planteado se modeliza a través de un diseño unifactorial totalmente aleatorizado de efectos fijos no-equilibrado.
- Variable respuesta: Densidad del fluido.
- Factor: Temperatura: Es un factor de Efectos fijos.
- Modelo no-equilibrado: Los niveles de los factores tienen distinto número de elementos.
-
¿Afecta la temperatura a la densidad del fluido?
El valor de F experimental 6.983, deja a su derecha un p-valor = 0.00419 inferior a 0.05, por lo que se rechaza la hipótesis nula de igualdad de medias. Concluyendo que existen diferencias significativas en la densidad del fluido en función de la modificación de la temperatura
2. Determinar qué temperaturas producen modificaciones significativas en la densidad media del fluido
Tukey multiple comparisons of means
95% family-wise confidence level
factor levels have been ordered
Fit: aov(formula = Densidad ~ Temperatura, data = propuesto1)
$`Temperatura`
diff lwr upr p adj
150-125 0.2200 -0.04410917 0.4841092 0.1184044
100-125 0.2400 -0.02410917 0.5041092 0.0807121
175-125 0.4375 0.15910449 0.7158955 0.0021907
100-150 0.0200 -0.22900452 0.2690045 0.9953076
175-150 0.2175 -0.04660917 0.4816092 0.1240769
175-100 0.1975 -0.06660917 0.4616092 0.1785203
3. Estudiar las hipótesis del modelo: Homocedasticidad, independencia y normalidad.
HOMOCEDASTICIDAD
Bartlett test of homogeneity of variances
data: propuesto1$Densidad and propuesto1$Temperatura
Bartlett’s K-squared = 0.69212, df = 3, p-value = 0.8751
NORMALIDAD
Shapiro-Wilk normality test
data: mod$residuals
W = 0.94639, p-value = 0.3712
Solución del Ejercicio Propuesto 1
Ejercicio Propuesto 2 (Resuelto)
Un laboratorio de reciclaje controla la calidad de los plásticos utilizados en bolsas. Se desea contrastar si existe variabilidad en la calidad de los plásticos que hay en el mercado. Para ello, se eligen al azar cuatro plásticos y se les somete a una prueba para medir el grado de resistencia a la degradación ambiental. De cada plástico elegido se han seleccionado ocho muestras y los resultados de la variable que mide la resistencia son los de la tabla adjunta.
 Figura 35: Tabla de datos del Ejercicio Propuesto2.doc
Figura 35: Tabla de datos del Ejercicio Propuesto2.doc
¿Qué conclusiones se deducen de este experimento?
Solución:
En este modelo, se supone que las variables τi son variables aleatorias normales independientes con media 0 y varianza común ![]() .
.
Df Sum Sq Mean Sq F value Pr(>F)
Plástico 3 69072 23024 17.23 1.55e-06 ***
Residuals 28 37411 1336
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
- Varianza de los residual: 37411
- Varianza entre los factores: 3957.625
- Varianza Total: 41368.625
Solución del Ejercicio Propuesto 2
Ejercicio Propuesto 3 (Resuelto)
Debido a la proliferación de los campos de golf y a la gran cantidad de agua que necesitan, un grupo de científicos estudia la calidad de varios tipos de césped para implantarlo en invierno en los campos de golf. Para ello, miden la distancia recorrida por una pelota de golf, en el campo, después de bajar por una rampa (para proporcionar a la pelota una velocidad inicial constante). El terreno del que disponen tiene mayor pendiente en la dirección norte-sur, por lo que se aconseja dividir el terreno en cinco bloques de manera que las pendientes de las parcelas individuales dentro de cada bloque sean las mismas. Se utilizó el mismo método para la siembra y las mismas cantidades de semilla. Las mediciones son las distancias desde la base de la rampa al punto donde se pararon las pelotas. En el estudio se incluyeron las variedades: Agrostis Tenuis (Césped muy fino y denso, de hojas cortas y larga duración), Agrostis Canina (Hoja muy fina, estolonífera. Forma una cubierta muy tupida), Paspalum Notatum (Hojas gruesas, bastas y con rizomas. Forma una cubierta poco densa), Paspalum Vaginatum (Césped fino, perenne, con rizomas y estolones).
 Figura 35: Tabla de datos del Ejercicio Propuesto 3.doc
Figura 35: Tabla de datos del Ejercicio Propuesto 3.doc
Se pide:
-
-
Identificar los elementos del estudio (factores, unidades experimentales, variable respuesta, etc.) y plantear detalladamente el modelo matemático utilizado en el experimento.
- ¿Son los bloques fuente de variación?
- Existen diferencias reales entre las distancias medias recorridas por una pelota de golf en los distintos tipos de césped?
- Estudiar las interacciones de los factores.
- Comprobar que se cumplen las hipótesis del modelo.
- Utilizando el método de Newman-Keuls, ¿qué tipo de césped ofrece menor resistencia al recorrido de las pelotas?
-
Solución:
1. Identificar los elementos del estudio (factores, unidades experimentales, variable respuesta, etc.) y plantear detalladamente el modelo matemático utilizado en el experimento.
-
-
- Variable respuesta: Distancia.
- Factor: Tipo_Césped que tiene cuatro niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Bloque: Bloques que tiene cinco niveles. Es un factor de efectos fijos ya que viene decidido qué niveles concretos se van a utilizar.
- Modelo completo: Los cuatro tratamientos se prueban en cada bloque exactamente una vez.
- Tamaño del experimento: Número total de observaciones (20).
-
Este experimento se modeliza mediante un diseño en Bloques completos al azar. El modelo matemático es:
![]() Expresión 27: Expresión del modelo del ejercicio propuesto 3
Expresión 27: Expresión del modelo del ejercicio propuesto 3
2. ¿Son los bloques fuente de variación?
Para realizar este supuesto en R debemos introducir primero los datos de forma correcta. Podemos introducir los datos directamente en R de forma manual o introducirlos previamente en un archivo de texto o Excel y leerlos en R.
En este caso lo hacemos en un archivo de texto:
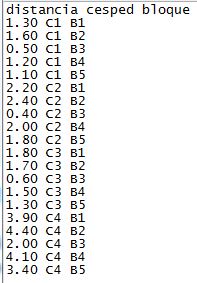
Figura 36: Tabla de datos del Ejercicio Propuesto 3.txt
Para cargar los datos utilizamos la función read.table indicando el nombre del archivo (que debe de estar en el directorio de trabajo) e indicando además que tiene cabecera.
Nota: La ruta hasta llegar al fichero varía en función del ordenador. Utilizar la orden setwd() para situarse en el directorio de trabajo
> setwd(“C:/Users/Usuario/Desktop/Datos”)
> propuesto3<- read.table(“propuesto3.txt”, header = TRUE)
> propuesto3$cesped= factor(propuesto3$cesped)
> propuesto3$bloque= factor(propuesto3$bloque)
Para calcular la tabla ANOVA primero hacemos uso de la función “aov”y a continuación mostramos un resumen de los resultados con la función “summary”
En la Tabla ANOVA, el valor del estadístico de contraste de igualdad de medias de tratamientos, F = 75.89 deja a su derecha un p-valor igual a 4.52e-08, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de tratamientos. Así, los tipos de césped influyen en las distancias recorridas por las pelotas. Es decir, existen diferencias significativas en las distancias recorridas por las pelotas entre los cuatro tipos de césped..
En esta Tabla ANOVA, también se observa que el valor del estadístico de contraste de igualdad de medias de bloques, F = 21.11 deja a su derecha un p-valor igual a 2.32e-05, menor que el nivel de significación del 5%, por lo que se rechaza la Hipótesis nula de igualdad de bloques. La eficacia de este diseño depende de los efectos de los bloques. En este caso este diseño es más eficaz que el diseño completamente aleatorizado y el contraste principal de las medias de los tratamientos será más sensible a las diferencias entre tratamientos. Por lo tanto la inclusión del factor bloque en el modelo es acertada. Así, las distancias recorridas por las pelotas dependen del tipo de terreno.
La interacción entre el factor bloque y los tratamientos vamos a estudiarla analíticamente mediante el Test de Interacción de un grado de Tukey
Para realizar este test en R tenemos que utilizar la library “daewr” y dentro de ella la función “Tukey1df”. De la siguiente forma:
> Tukey1df(propuesto3)
6. Utilizando el método de Duncan y Newman-Keuls, ¿qué tipo de césped ofrece menor resistencia al recorrido de las pelotas?
Para poder hacer uso de ambos contrastes en R tenemos que instalar en primer lugar el paquete “agricolae”
> (duncan=duncan.test(mod, “cesped” , group = T))
> SNK.test(mod, “cesped”, console =TRUE)
Ejercicio Propuesto 4 (Resuelto)
Consideremos de nuevo el ejercicio propuesto 3 sobre un grupo de científicos que estudia la calidad de varios tipos de césped para implantarlo en invierno en los campos de golf. Para ello, miden la distancia recorrida por una pelota de golf, en el campo, después de bajar por una rampa (para proporcionar a la pelota una velocidad inicial constante). El terreno del que disponen tiene mayor pendiente en la dirección norte-sur, por lo que se aconseja dividir el terreno en cinco bloques de manera que las pendientes de las parcelas individuales dentro de cada bloque sean las mismas. Se utilizó el mismo método para la siembra y las mismas cantidades de semilla. Las mediciones son las distancias desde la base de la rampa al punto donde se pararon las pelotas, y al realizar dichas mediciones no se han podido obtener una para cada combinación de tipo de césped y tipo de terreno, sino que sólo se han podido realizar con tres de las variedades del césped en cada uno de los bloques de terreno. Para controlar el efecto del tipo de terreno deciden utilizar un diseño en bloques incompletos. En el estudio se incluyeron las variedades: Agrostis Tenuis (Césped muy fino y denso, de hojas cortas y larga duración), Agrostis Canina (Hoja muy fina, estolonífera. Forma una cubierta muy tupida), Paspalum Notatum (Hojas gruesas, bastas y con rizomas. Forma una cubierta poco densa), Paspalum Vaginatum (Césped fino, perenne, con rizomas y estolones).
 Figura 36: Tabla de datos del Ejercicio Propuesto 4.doc
Figura 36: Tabla de datos del Ejercicio Propuesto 4.doc
Se pide:
1. Identificar los elementos del estudio (factores, unidades experimentales, variable respuesta, etc.) y plantear detalladamente el modelo matemático utilizado en el experimento.
2. ¿Son los bloques fuente de variación?
3. Existen diferencias reales entre las distancias medias recorridas por una pelota de golf en los distintos tipos de césped?
4. Comprobar que se cumplen las hipótesis del modelo.
5. Utilizando el método de Newman-Keuls, ¿qué tipo de cesped ofrece menor resistencia al recorrido de las pelotas?
Solución
2. ¿Son los bloques fuente de variación?
El p-valor 0.035 menor que el nivel de significación 0.05, por lo que se rechaza la hipótesis nula de igualdad de bloques y concluimos que los bloques son una fuente de variación.
3. Existen diferencias reales entre las distancias medias recorridas por una pelota de golf en los distintos tipos de césped?
El valor del estadístico de contraste de igualdad de tipo de césped, F = 3.727, deja a su derecha un p-valor 0.1540, mayor que el nivel de significación del 5%, por lo que no se rechaza la Hipótesis Nula de igualdad de tratamientos. Por lo tanto no hay diferencias reales entre las distancias medias recorridas por una pelota de golf en los distintos tipos de césped ya que el p-valor es mayor que 0.05.
5. Utilizando el método de Newman-Keuls, ¿qué tipo de cesped ofrece menor resistencia al recorrido de las pelotas?
En la tabla se muestran los subgrupos formados de medias iguales al utilizar el método de Newman-Keuls. Hay dos subconjuntos que se diferencian entre sí. Por una parte el formado por el tipo de césped C4 y por otra parte el subgrupo formado por los tipos de césped: C3, C2 y C1. También se observa que el tipo de césped donde la distancia recorrida es más grande es el C4 con una distancia de 3.96667 y la distancia más corta es de 1.2 en el césped C1.
Solución del Ejercicio Propuesto 4
Ejercicio Propuesto 5 (Resuelto)
Un investigador quiere evaluar la productividad de cuatro variedades de aguacates, A, B, C y D. Para ello decide realizar el ensayo en un terreno que posee un gradiente de pendiente de oriente a occidente y además, diferencias en la disponibilidad de Nitrógeno de norte a sur, para controlar los efectos de la pendiente y la disponibilidad de Nitrógeno, utilizó un diseño de cuadrado latino, los datos corresponden a la producción en kg/parcela.
 Figura 37: Tabla de datos del Ejercicio Propuesto 5.doc
Figura 37: Tabla de datos del Ejercicio Propuesto 5.doc
Responder a las siguientes cuestiones:
-
¿Se puede afirmar que la productividad media de las cuatro variedades de aguacate es la misma?
-
¿Qué supuestos han de verificarse?
- ¿Se obtiene la misma producción con las cuatro variedades de aguacate? En caso negativo, analizar mediante el procedimiento de Tukey y Newman-Keuls, con qué variedad de aguacate hay mayor producción.
Solución:
1. ¿Se puede afirmar que la productividad media de las cuatro variedades de aguacate es la misma?
El análisis de la productividad de las variedades de aguacate corresponde al análisis de un factor con 4 niveles. Dado que en el estudio intervienen dos fuentes de variación: la Disponibilidad de Nitrógeno y la Pendiente, se consideran dos factores de bloque, cada uno de ellos con 4 niveles.
Se pretende, entonces dar respuesta al contraste:
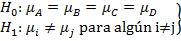 Expresión 28: Contraste de hipótesis
Expresión 28: Contraste de hipótesis
- Variable respuesta: Productividad
- Factor: Variedad de aguacate. Es un factor de efectos fijos ya que desde el principio se establecen los niveles concretos que se van a analizar.
- Bloques: Disponibilidad de Nitrógeno y Pendiente, ambos con 4 niveles y ambos de efectos fijos.
- Tamaño del experimento: Número total de observaciones (42) .
Observando los valores de los p-valores, 1.70e-05, 3.92e-09 y 2.13e-08; menores respectivamente que el nivel de significación del 5%, deducimos que los tres efectos son significativos. Tanto las variedades de aguacates utilizadas, como la pendiente del terreno y la disponibilidad de nitrógeno influyen en la productividad de los aguacates
2. ¿Qué supuestos han de verificarse?
3. ¿Se obtiene la misma producción con las cuatro variedades de aguacate? En caso negativo, analizar mediante el procedimiento de Tukey y Newman-Keuls, con qué variedad de aguacate hay mayor producción.
La tabla de comparaciones múltiples muestra los intervalos simultáneos construidos por el método de Tukey para cada posible combinación de variedades de aguacates. En la tabla se muestra un resumen de las comparaciones de cada tratamiento con los restantes. Es decir, aparecen comparadas dos a dos las cuatro medias de los tratamientos.
En esta tabla, las columnas:
- diff: muestra las medias de cada par
- p adj: muestra los p-valores de los contrastes, que permiten conocer si la diferencia entre cada pareja de medias es significativa al nivel de significación considerado (en este caso 0.05)
- lwr y upr: proporcionan los intervalos de confianza al 95% para cada diferencia.
Así por ejemplo, si comparamos la concentración media correspondiente a las variedades A Y B, tenemos una diferencia entre ambas medias de 33.75, un p-valor (Sig.) de 0.0001393 significativo. Por lo tanto, las producciones medias de las variedades A y B pueden considerarse distintas estadísticamente y un intervalo de confianza con un límite inferior 23.1507168 y un límite superior 44.34928 y por lo tanto no contiene al cero de lo que también deducimos que hay diferencias significativas entre estas dos variedades de aguacate.
Como se puede observar, todos los intervalos de confianza construidos para las diferencias entre las producciones medias de las variedades no contienen al 0, excepto el correspondiente a la pareja de variedades de aguacates A y D. Lo que significa que todas las producciones medias pueden considerarse distintas estadísticamente excepto las producciones medias correspondientes a las variedades A y D. Se deduce que únicamente no se observan diferencias significativas entre las producciones de las variedades de aguacates A y D (P-valor = 0.4289199).
Solución del Ejercicio Propuesto 5
Ejercicio Propuesto 6 (Resuelto)
Consideremos de nuevo el ejercicio propuesto 5 del investigador que quiere evaluar la productividad de cuatro variedades de aguacate, A, B, C y D. Para ello, decide realizar el ensayo en un terreno que posee un gradiente de pendiente de oriente a occidente y además, diferencias en la disponibilidad de Nitrógeno de norte a sur. Se seleccionan cuatro disponibilidades de nitrógeno, pero sólo dispone de tres gradientes de pendiente. Para controlar estas posibles fuentes de variabilidad, el investigador decide utilizar un diseño en cuadrado de Youden con cuatro filas, las cuatro disponibilidades de Nitrógeno (NI, N2, N3, N4), tres columnas, los tres gradientes de pendientes (P1, P2, P3) y cuatro letras latinas, las variedades de aguacates (A, B, C, D). Los datos corresponden a la producción en kg/parcela.
 Figura 38: Tabla de datos del Ejercicio Propuesto 6.doc
Figura 38: Tabla de datos del Ejercicio Propuesto 6.doc
Responder a las siguientes cuestiones:
-
Estudiar cuál es el tipo de diseño adecuado a este experimento y escribir el modelo matemático asociado.
-
¿Se puede afirmar que la productividad media de las cuatro variedades de aguacate es la misma?
-
Comprobar la hipótesis de homocedasticidad
- ¿Se obtiene la misma producción con las cuatro variedades de aguacate? En caso negativo, analizar mediante el procedimiento de Duncan, con qué variedad de aguacate hay mayor producción.
Solución:
El análisis de la productividad de las variedades de aguacate corresponde al análisis de un factor con 4 niveles. Dado que en el estudio intervienen dos fuentes de variación: la Disponibilidad de Nitrógeno y la Pendiente, se consideran dos factores de bloque, el primero con 4 niveles y el segundo con tres niveles.
Se pretende, entonces dar respuesta al contraste:
![]() Expresión 28: Contraste de hipótesis
Expresión 28: Contraste de hipótesis
- Variable respuesta: Productividad.
- Factor: Variedad de aguacate. Es un factor de efectos fijos ya que desde el principio se establecen los niveles concretos que se van a analizar.
- Bloques: Disponibilidad de Nitrógeno y Pendiente, con 4 y 3 niveles, respectivamente y ambos de efectos fijos.
- Tamaño del experimento: Número total de observaciones: 12 .
El p-valor, 0.0241, es menor que el nivel de significación del 5%, deducimos que el factor principal: Variedades del aguacate es significativo.
El p-valor, 0.0586, es mayor que el nivel de significación del 5%, deducimos que el Factor Bloque: Pendiente no es significativo.
El p-valor es 0.0138; menor que el nivel de significación del 5%, deducimos que Factor Bloque: Nitrógeno es significativo.
Los p-valores del factor tratamiento, Variedad de aguacate (0.6145), del factor bloque Pendiente (0.779) y del factor bloque Nitrógeno (0.2759) son mayores que 0.05, por lo tanto no se puede rechazar la hipótesis de homogeneidad de la varianza del tratamiento y de los bloques.
4. ¿Se obtiene la misma producción con las cuatro variedades de aguacate? En caso negativo, analizar mediante el procedimiento de Duncan, con qué variedad de aguacate hay mayor producción.
En la tabla se muestran los subgrupos formados de medias iguales al utilizar el método de Duncan. Hay tres subconjuntos que se diferencian entre sí. Por una parte el formado por la variedad de aguacate B y D, el subgrupo formado por D y C y el formado por A y C. También se observa que la mayor productividad de aguacate es la del tipo B, con una producción de 901.3333 Kg por parcela y la menor el tipo A, 732.0000 kg por parcela.
Solución del Ejercicio Propuesto 6
Ejercicio Propuesto 7 (Resuelto)
En un invernadero se está estudiando el crecimiento de determinadas plantas, para ello se quiere controlar los efectos del terreno, abono, insecticida y semilla. El estudio se realiza con cuatro tipos de semillas diferentes que se plantan en cuatro tipos de terreno, se les aplican cuatro tipos de abonos y cuatro tipos de insecticidas. La asignación de los tratamientos a las plantas se realiza de forma aleatoria. Para controlar estas posibles fuentes de variabilidad se decide plantear un diseño por cuadrados greco-latinos como el que se muestra en la siguiente tabla, donde las letras griegas corresponden a los cuatro tipos de semilla y las latinas a los abonos.
 Figura 39: Tabla de datos del Ejercicio Propuesto 7.doc
Figura 39: Tabla de datos del Ejercicio Propuesto 7.doc
Responder a las siguientes cuestiones:
-
Estudiar cuál es el tipo de diseño adecuado a este experimento y escribir el modelo matemático asociado.
- ¿Se puede afirmar que el crecimiento de las plantas es el mismo para los cuatro tipos de abonos?¿Y con los distintos insecticidas?
-
¿Existen diferencias significativas en el crecimiento de las plantas con las distintas semillas? ¿Y el tipo de tierra influye en dicho crecimiento?
-
¿Con qué tipo de semilla se produce el mayor crecimiento de las plantas?
- ¿El crecimiento de las plantas es el mismo utilizando al mismo tiempo los abonos A y B que utilizando los abonos C y D?
Solución:
- Estudiar cuál es el tipo de diseño adecuado a este experimento y escribir el modelo matemático asociado.
2. ¿Se puede afirmar que el crecimiento de las plantas es el mismo para los cuatro tipos de abonos? ¿Y con los distintos insecticidas?
El mayor crecimiento de las plantas se produce con el Abono D siendo la altura que alcanza de 11.75 y la menor altura (7.75) la alcanza con el tipo de abono C
La menor altura (7.5) la alcanza cuando se le suministra el Insecticida 1.
3. ¿Existen diferencias significativas en el crecimiento de las plantas con las distintas semillas? ¿Y el tipo de tierra influye en dicho crecimiento?
Comprobamos que únicamente hay diferencias significativas entre los tipos de semillas alfa-gamma (p-valor = 0.0139) y entre alfa-beta (p-valor =0.0171).
Hay dos grupos de terrenos que difieren significativamente, por un lado el grupo formado por los tipos de terrenos 1,2 y 4 y por otra parte el grupo formado un solo tipo de terreno, el tipo de terreno 3. El mayor crecimiento de las plantas se produce en el tipo de terreno 1 con un crecimiento de 11 u.c.
4. ¿Con qué tipo de semilla se produce el mayor crecimiento de las plantas?
El mayor crecimiento de la planta se produce con el tipo de semilla alfa (11.50 u.c.)
5. ¿El crecimiento de las plantas es el mismo utilizando al mismo tiempo los abonos A y B que utilizando los abonos C y D?
Hay diferencias significativas en el crecimiento utilizando los abonos C y D (P-valor = 0.0094), pero no las hay con los abonos A y B (P-valor= 0.064).
Solución del Ejercicio Propuesto 7
Ejercicio Propuesto 8 (Resuelto)
Se realiza un estudio sobre el efecto que produce la descarga de aguas residuales de una planta sobre la ecología del agua natural de un río. En el estudio se utilizaron dos lugares de muestreo. Un lugar está aguas arriba del punto en el que la planta introduce aguas residuales en la corriente; el otro está aguas abajo. Se tomaron muestras durante un periodo de cuatro semanas y se obtuvieron los datos sobre el número de diatomeas halladas. Los datos se muestran en la tabla adjunta:
 Figura 41: Tabla de datos del Ejercicio Propuesto8.doc
Figura 41: Tabla de datos del Ejercicio Propuesto8.doc
Responder a las siguientes cuestiones:
-
-
Identificar el diseño adecuado a este experimento, escribir el modelo matemático y explicar los distintos elementos que intervienen.
-
Estudiar si la semana y el lugar son factores determinantes en el número de diatomeas halladas en el agua del río. ¿Hay posibilidad que una semana sea más recomendable en un lugar del río en concreto y no lo sea en el otro lugar?
-
Estudiar en qué semana se producen menos contaminación en el río, utilizando el método de Duncan.
-
Estudiar en qué lugar del río se producen menos diatomeas.
-
Solución:
1. Identificar el diseño adecuado a este experimento, escribir el modelo matemático y explicar los distintos elementos que intervienen
2. Estudiar si la semana y el lugar son factores determinantes en el número de diatomeas halladas en el agua del río. ¿Hay posibilidad que una semana sea más recomendable en un lugar del río en concreto y no lo sea en el otro lugar?
Son significativos los efectos de los dos factores, pero no es significativo la interacción. Ambos son factores determinantes en el número de diatomeas halladas en el agua del río.
El número de diatomeas (533.250) es mayor en la semana 4 y menor en la semana 3 (119.875). Hay dos subgrupos diferenciados. Un subgrupo está formado por las semanas 2 y 4 y el otro subgrupo por las semanas 1 y 3.
3. Estudiar en qué semana se producen menos contaminación en el río, utilizando el método de Duncan
Se produce menos contaminación en aguas abajo, con un número de diatomeas de 239.50. Y como hemos dicho anteriormente hay diferencias significativas entre el número de diatomeas que se producen en aguas arribas del rio y las que se producen en aguas abajo del rio
4. Estudiar en qué lugar del río se producen menos diatomeas.
El número de diatomeas (533.250) es mayor en la semana 4 y menor en la semana 3 (119.875).
Solución del Ejercicio Propuesto 8
Ejercicio Propuesto 9 (Resuelto)
La cotinina es uno de los principales metabolitos de la nicotina. Actualmente se le considera el mejor indicador de la exposición al humo de tabaco. Se ha realizado un estudio con distintas marcas de tabaco distinguiendo principalmente entre negro y rubio para detectar las posibles diferencias en el nivel de nicotina de personas expuestas al humo de tabaco. Para ello, se han analizado personas de distintas edades (niños, jóvenes y adultos) y se ha distinguido entre mujeres y hombres. Se han obtenido los datos de la siguiente tabla sobre el nivel de nicotina en miligramos por mililitro.
 Figura 42: Tabla de datos del Ejercicio Propuesto9.doc
Figura 42: Tabla de datos del Ejercicio Propuesto9.doc
Responder a las siguientes cuestiones:
-
Identificar el diseño adecuado a este experimento, escribir el modelo matemático y explicar los distintos elementos que intervienen.
-
Contrastar la hipótesis nula de no interacción entre los factores. Adecuar el modelo al resultado de las interacciones y contrastar los efectos principales.
-
¿Hay diferencias significativas en el nivel de nicotina en las distintas edades?¿En qué edad el nivel de nicotina es mayor?
- ¿El tipo de tabaco es un factor determinante en el nivel de nicotina?
-
Comparar el nivel medio de nicotina entre las mujeres y los hombres. ¿Se detectan diferencias significativas?
Solución:
1. Identificar el diseño adecuado a este experimento, escribir el modelo matemático y explicar los distintos elementos que intervienen
2. Contrastar la hipótesis nula de no interacción entre los factores. Adecuar el modelo al resultado de las interacciones y contrastar los efectos principales
El único efecto significativo son las distintas edades.
Al no ser significativa ninguna de las interacciones, realizamos de nuevo el ANOVA sufrimiento la interacción entre los tres factores.
De nuevo el único efecto significativo es la Edad. Realizamos de nuevo el ANOVA suprimiendo la interacción de orden 2 Sexo*Tabaco.
De nuevo el mismo resultado, suprimimos la interacción Tabaco*Edades.
Son significativos el efecto de la Edad y el efecto de la interacción del Sexo por la Edad.
3. ¿Hay diferencias significativas en el nivel de nicotina en las distintas edades? ¿En qué edad el nivel de nicotina es mayor?
Si hay diferencias significativas del nivel de nicotina en las distintas edades (P-valor es 0.0441).
El nivel de nicotina es mayor en los Adultos (451.375 miligramos por mililitro).
4. ¿El tipo de tabaco es un factor determinante en el nivel de nicotina?
El tipo de tabaco no es determinante en el nivel de nicotina (P-valor = 0.9415).
5. Comparar el nivel medio de nicotina entre las mujeres y los hombres. ¿Se detectan diferencias significativas?
No hay diferencias significativas en el nivel de nicotina entre las mujeres y los hombres (P-valor = 0.7328)
Las mujeres y los hombres forman un único grupo donde no se aprecian diferencias significativas. Es mayor el nivel de nicotina entre las mujeres (365.1667 miligramos por mililitro).
Solución del Ejercicio Propuesto 9
Autora: Ana María Lara Porras. Universidad de Granada. (2018).