CONTRASTES DE HIPÓTESIS
Objetivos
- Resolver contrastes de hipótesis para la media de una población normal con varianza conocida
- Resolver contrastes de hipótesis para la media de una población normal con varianza desconocida
- Resolver contrastes de hipótesis para una proporción
- Resolver contrastes de hipótesis para la diferencia de medias en dos poblaciones normales independientes con varianzas desconocidas
- Suponiendo que las varianzas, aun siendo desconocidas, son iguales en las dos poblaciones
- Suponiendo que las varianzas son diferentes en las dos poblaciones
- Resolver contrastes de hipótesis para la diferencia de medias en dos poblaciones normales relacionadas
- Resolver contrastes de hipótesis para la diferencia de proporciones
- Resolver contrastes de hipótesis no-paramétricos de independencia para variables cualitativas
- Resolver contrastes de hipótesis no-paramétricos de bondad de ajuste de distribuciones
- Resolver contrastes de hipótesis no-paramétricos de aleatoriedad
- Resolver contrastes de hipótesis no-paramétricos de dos muestras independientes y de dos muestras relacionadas.
- APÉNDICE: Introducción al Análisis de datos categóricos: Tablas de Contingencia.
Conceptos básicos
Contraste de hipótesis. Un contraste de hipótesis (también conocido como test de hipótesis) es una técnica estadística que se utiliza para comprobar la validez de una afirmación en base a la información recogida en una muestra de observaciones. Es un proceso estadístico mediante el cual se investiga si una propiedad que se supone que cumple una población es compatible con lo observado en una muestra de dicha población. Es un procedimiento que permite elegir una hipótesis de trabajo de entre dos posibles y antagónicas.
Hipótesis Estadística. Todo contraste de hipótesis se basa en la formulación de dos hipótesis exhaustivas y mutuamente exclusivas:
- Hipótesis nula (\( H_0 \))
- Hipótesis alternativa (\( H_1 \))
La afirmación cuya validez se pretende comprobar recibe el nombre de hipótesis nula y se denota mediante \( H_0 \). La hipótesis nula de un contraste habitualmente hace referencia al valor poblacional de un parámetro o a la distribución de probabilidad de una variable. En los casos en los que la información de la muestra no apoya la hipótesis nula, se da por veraz una afirmación alternativa, que se conoce como hipótesis alternativa, y se denota por \( H_1 \). La hipótesis alternativa es la negación de la hipótesis nula. Así, por ejemplo, en un contraste sobre los valores poblaciones de un parámetro, en la hipótesis alternativa se recogen todos los posibles valores del parámetro que no figuran en la hipótesis nula. Igualmente, cuando se contrasta la distribución de probabilidad de una variable, en la hipótesis alternativa se incluyen todas las distribuciones de probabilidad que no se han considerado en la hipótesis nula. De aquí se deduce que la hipótesis nula y la hipótesis alternativa son exhaustivas y mutuamente excluyentes.
La hipótesis \( H_0 \) es la que se desea contrastar. Consiste generalmente en una afirmación concreta sobre la forma de una distribución de probabilidad o sobre el valor de alguno de los parámetros de esa distribución. El nombre de “nula” significa “sin valor, efecto o consecuencia”, lo cual sugiere que \( H_0 \) debe identificarse con la hipótesis de no cambio (a partir de la opinión actual); no diferencia, no mejora, etc. \( H_0 \) representa la hipótesis que mantendremos a no ser que los datos indiquen su falsedad, y puede entenderse, por tanto, en el sentido de “neutra”. La hipótesis \( H_0 \) nunca se considera probada, aunque puede ser rechazada por los datos. Por ejemplo, la hipótesis de que dos poblaciones tienen la misma media puede ser rechazada fácilmente cuando ambas difieren mucho, analizando muestras suficientemente grandes de ambas poblaciones, pero no puede ser “demostrada” mediante muestreo, puesto que siempre cabe la posibilidad de que las medias difieran en una cantidad lo suficientemente pequeña para que no pueda ser detectada, aunque la muestra sea muy grande. Dado que descartaremos o no la hipótesis nula a partir de muestras obtenidas (es decir, no dispondremos de información completa sobre la población), no será posible garantizar que la decisión tomada sea la correcta.
La hipótesis \( H_1 \) es la negación de la nula. Incluye todo lo que \( H_0 \) excluye.
¿Qué asignamos como \( H_0 \) y \( H_1 \)?
La hipótesis \( H_0 \) asigna un valor específico al parámetro en cuestión y por lo tanto “el igual” siempre forma parte de \( H_0 \).
La idea básica de la prueba de hipótesis es que los hechos tengan probabilidad de rechazar \( H_0 \). La hipótesis \( H_0 \) es la afirmación que podría ser rechazada por los hechos. El interés del investigador se centra, por lo tanto, en la \( H_1 \).
La regla de decisión. Es el criterio que vamos a utilizar para decidir si la hipótesis nula planteada debe o no ser rechazada. Este criterio se basa en la partición de la distribución muestral del estadístico de contraste en dos regiones o zonas mutuamente excluyentes: Región crítica o región de rechazo y Región de no-rechazo.
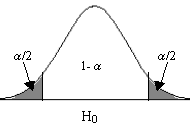
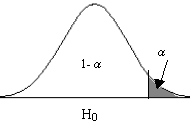
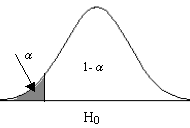
Región de no-rechazo. Es el área de la distribución muestral que corresponde a los valores del estadístico de contraste próximos a la afirmación establecida en \( H_0 \). Es decir, los valores del estadístico de contraste que nos conducen a decidir \( H_0 \). Es por tanto, el área correspondiente a los valores del estadístico de contraste que es probable que ocurran si \( H_0 \) es verdadera. Su probabilidad se denomina nivel de confianza y se representa por 1 – α .
Región de rechazo o región crítica. Es el área de distribución muestral que corresponde a los valores del estadístico de contraste que se encuentran tan alejados de la afirmación establecida en \( H_0 \), que es muy poco probable que ocurran si \( H_0 \) es verdadera. Su probabilidad se denomina nivel de significación o nivel de riesgo y se representa con la letra α .
Ya definidas las dos zonas, la regla de decisión consiste en rechazar \( H_0 \) si el estadístico de contraste toma un valor perteneciente a la zona de rechazo, o mantener \( H_0 \) si el estadístico de contraste toma un valor perteneciente a la zona de no-rechazo.
El tamaño de las zonas de rechazo y no-rechazo se determina fijando el valor de α, es decir, fijando el nivel de significación con el que se desea trabajar. Se suele tomar un 1% o un 5%.
La forma de dividir la distribución muestral en zona de rechazo y de no-rechazo depende de si el contraste es bilateral o unilateral. La zona crítica debe situarse donde puedan aparecer los valores muestrales incompatibles con \( H_0 \).
Estadístico de contraste. Un estadístico de contraste es un resultado muestral que cumple la doble condición de:
- Proporcionar información empírica relevante sobre la afirmación propuesta en la \( H_0 \).
- Poseer una distribución muestral conocida
Tipos de contrastes.
Contrastes paramétricos: Conocida una v.a. con una determinada distribución, se establecen afirmaciones sobre los parámetros de dicha distribución.
Contrastes no paramétricos: Las afirmaciones establecidas no se hacen en base a la distribución de las observaciones, que a priori es desconocida.
Tipos de hipótesis del contraste.
Existen dos tipos de contrastes de hipótesis en función de la forma que adopten las hipótesis: los contrastes bilaterales y los contrastes unilaterales. En los contrastes bilaterales la hipótesis nula es una igualdad mientras que en los contrastes unilaterales en la hipótesis nula aparece una desigualdad no estricta. Cualquiera que sea el caso, es importante notar que en la hipótesis nula siempre debe aparecer un signo de igualdad, ya sea como una igualdad en sí (=) o como una desigualdad no estricta (\( \leq \) o \( \geq \)). A modo de ejemplo, veamos los tipos de contrastes de hipótesis para la media de una variable que pueden darse.
\( \begin{array} {|c|} \hline Contraste \hspace{.1cm} bilateral \\ \hline H_0 \equiv \mu = \mu_0 \\ \hline H_1 \equiv \mu \neq \mu_0 \\ \hline \end{array} \) \( \hspace{2cm} \begin{array} {|c||} \hline Contrastes \hspace {.1cm}unilaterales \\ \hline H_0 \equiv \mu \geq \mu_0 \hspace{2cm} H_0 \equiv \mu \leq \mu_0 \\ \hline H_1 \equiv \mu < \mu_0 \hspace{2cm} H_1 \equiv \mu > \mu_0 \\ \hline \end{array} \)
Expresión 1: Tipo de contrastes de hipótesis
El planteamiento de un contraste de hipótesis es el paso previo a su resolución. Plantear un contraste de hipótesis consiste en definir la hipótesis nula y la hipótesis alternativa.
Una vez planteado el contraste, se calcula el valor del estadístico de contraste. Un estadístico de contraste es una función de los datos muestrales cuya distribución de probabilidad es conocida en las condiciones que establece la hipótesis nula. Es decir, el estadístico de contraste, T, se calcula a partir de una muestra de tamaño n, \( X_1, X_2, \cdots , X_{n} \), de la variable de interés, X, como \( T = f( X_1, X_2, \cdots , X_{n}) \). En función del valor de T , optaremos por rechazar, o no, la hipótesis nula. Concretamente, los valores de T con probabilidades pequeñas de haber sido obtenidos bajo las condiciones que establece la hipótesis nula nos harán pensar que dicha hipótesis no es cierta en realidad y, consecuentemente, nos llevarán a rechazarla. El conjunto de todos los valores del estadístico de contraste que nos llevan a rechazar la hipótesis nula recibe el nombre de región de rechazo o región crítica. Por el contrario, el conjunto de los valores del estadístico de contraste que nos hacen no rechazar la hipótesis nula se denomina región de aceptación. La localización de la región crítica depende del tipo de contraste que se plantee, tal y como se muestra en la siguiente figura.
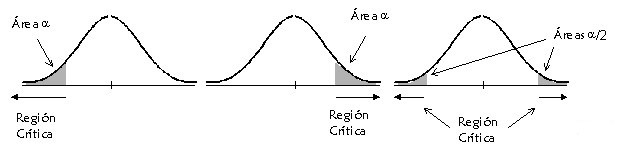
Figura 1: Localización de la región crítica
Las dos primeras imágenes muestran las regiones críticas para contrastes unilaterales. Concretamente, la primera imagen se corresponde con el caso de un contraste de hipótesis con hipótesis alternativa del tipo <, mientras que la región crítica de la segunda imagen se corresponde con un contraste de hipótesis con hipótesis alternativa del tipo >. Por último, en la tercera imagen representa la región crítica para un contraste con hipótesis alternativa del tipo \( \neq \). En cualquier caso, los valores de la región crítica son aquellos que menos probabilidad tienen de ocurrir suponiendo cierta la hipótesis nula.
Hipótesis simples: La hipótesis asigna un único valor al parámetro desconocido, \( H \equiv \theta = \theta_0 \)
Hipótesis compuestas: La hipótesis asigna varios valores posibles al parámetro desconocido, \( H \equiv \theta \in ( \theta_1, \theta_2) \)
En términos generales: Dada una variable aleatoria \( X \) que se distribuye según una ley de probabilidad \( Ϝ(\theta) \) que depende de un parámetro θ. Supongamos que el parámetro \( \theta \) es desconocido y que \( \theta_0 \) es el valor propuesto para \( \theta \). El contraste consiste en elegir, en alguno de los contrastes siguientes, entre la hipótesis \( H_0 \) o \( H_1 \).
\( \begin{array}{ccccc} H_0 \equiv \theta \leq \theta_0 & & H_0 \equiv θ \geq θ_0 & & H_0 \equiv θ = θ_0 \\ & o & & o & \\ H_1 \equiv \theta > \theta_0 & & H_1 \equiv θ < θ_0 & & H_1 \equiv θ \neq θ_0 \end{array} \)
Nota: Consideramos la hipótesis \( H_0 \) simple y la hipótesis \( H_1 \) compuesta.
- En los dos primeros contrastes, en los que la hipótesis alternativa es: \( H_1≡ θ>θ_0 \) o \( H_1 ≡ θ<θ_0 \), se dice que la Hipótesis Alternativa es Unilateral, ya que los posibles valores de \( θ \) bajo \( H_1 \) están situados a un lado del valor propuesto bajo \( H_0 \) y la región crítica recibe el nombre de Región crítica o de Rechazo Unilateral. (La hipótesis \( H_1 \) da lugar a una región crítica a un solo lado del valor del parámetro).
- En el tercer contraste, en el que la hipótesis alternativa es de la forma \( H_1≡ θ \neq θ_0 \), se dice que la Hipótesis Alternativa es Bilateral y la región crítica también recibe el nombre de Región Crítica Bilateral. (La hipótesis \( H_1 \) da lugar a una región crítica a ambos lados del valor del parámetro).
\( \begin{array}{||c|c||} \hline \begin{array}{c}H_0 \equiv \theta = \theta_0 \\ H_1 \equiv \theta \neq \theta_0 \end{array}& Simple – Compuesta \\ \hline \begin{array}{c}H_0 \equiv \theta \leq \theta_0 \\ H_1 \equiv \theta > \theta_0 \end{array}& Compuesta – Compuesta \\ \hline \begin{array}{c}H_0 \equiv \theta \geq \theta_0 \\ H_1 \equiv \theta < \theta_0 \end{array} & Compuesta – Compuesta \\ \hline \end{array} \)
Expresión 2: Tipos de Hipótesis
El tamaño de la región de rechazo lo establece el investigador. Es decir, el investigador decide a partir de qué valor del estadístico de contraste va a rechazar la hipótesis nula. O en otras palabras, identifica cuáles son los valores que son poco probables de ocurrir bajo la hipótesis nula. El valor del estadístico de contraste a partir del cual se rechaza la hipótesis nula recibe el nombre de valor crítico. A la probabilidad de los valores de la región crítica se le conoce como nivel de significación y se denota mediante α. Al valor 1-α se le conoce como nivel de confianza.
La resolución del contraste se hace en función de un criterio que se conoce como regla de decisión. La regla de decisión nos dice que se ha de rechazar la hipótesis nula en favor de la hipótesis alternativa cuando el valor del estadístico de contraste caiga dentro de la región de rechazo. En caso contrario, no se rechazará la hipótesis nula y se considerará cierta. En otras palabras, rechazaremos la hipótesis nula siempre y cuando el valor del estadístico de contraste sea mayor al valor crítico.
Equivalentemente, se puede resolver un contraste a partir de una probabilidad que recibe el nombre de p-valor. El p-valor de un contraste de hipótesis nos indica cuál es la probabilidad de obtener un valor del estadístico de contraste tanto o más “extraño” que el que se ha obtenido suponiendo que la hipótesis nula es cierta. Por tanto, p-valores pequeños nos llevarán a rechazar la hipótesis nula. Concretamente, si el p-valor obtenido es más pequeño que el nivel de significación, rechazaremos la hipótesis nula. En caso contrario, no podremos rechazar la hipótesis nula y la consideraremos verdadera.
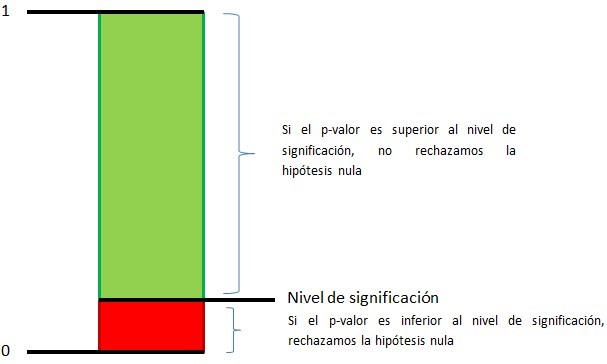
Figura 2: Representación del rechazo y no rechazo de la hipótesis nula en función del p-valor
La Reglas de decisión.
- Contrastes bilaterales: Si la hipótesis alternativa da lugar a una región crítica “a ambos lados” del valor del parámetro, diremos que el test es bilateral o de dos colas.
Se rechaza \( H_0 \) si el estadístico de contraste cae en la zona crítica, es decir, si el estadístico de contraste toma un valor tan grande o tan pequeño que la probabilidad de obtener un valor tan extremo o más que el encontrado es menor que α /2.
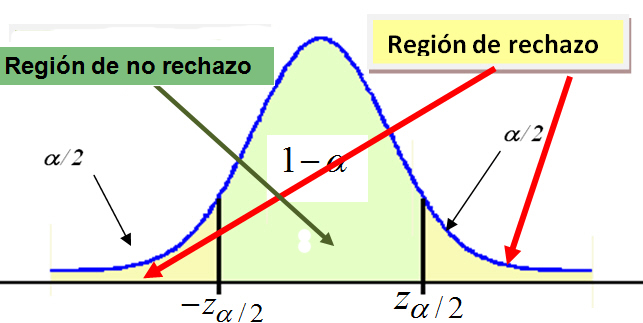 Figura 3: Regiones de rechazo y no rechazo
Figura 3: Regiones de rechazo y no rechazo
- Contraste unilateral: Si la hipótesis alternativa da lugar a una región crítica “a un solo lado del valor del parámetro”, diremos que el test es unilateral o de una sola cola
Se rechaza \( H_0 \) si el estadístico de contraste cae en la zona crítica, es decir, si toma un valor tan grande que la probabilidad de obtener un valor como ese o mayor es menor que α .
|
Contraste bilateral \( H_0 \equiv \theta = \theta_0 \) \( H_1 \equiv \theta \neq \theta_0 \) |
Contraste unilateral: Cola a la derecha \( H_0 \equiv \theta ≤ \theta_0 \) \( H_1 \equiv \theta > \theta_0 \) |
Contraste unilateral: Cola a la izquierda \( H_0 \equiv \theta ≥ \theta_0 \) \( H_1 \equiv \theta < \theta_0 \) |
La decisión:
Planteada la hipótesis, formulados los supuestos, definido el estadístico de contraste y su distribución muestral, y establecida la regla de decisión, el paso siguiente es obtener una muestra aleatoria de tamaño n, calcular el estadístico de contraste y tomar una decisión:
- Si es estadístico de contraste cae en la zona crítica se rechaza \( H_0 \).
- Si es estadístico cae en la zona de no rechazo se mantiene \( H_0 \).
Si rechazamos \( H_0 \) afirmamos que la hipótesis es falsa, es decir, que afirmamos con una probabilidad α de equivocarnos que esa hipótesis es falsa. Por el contrario, si no la rechazamos, no estamos afirmando que la hipótesis sea verdadera. Simplemente que no tenemos evidencia empírica suficiente para rechazarla y que se considera compatible con los datos.
Como conclusión, si se mantiene o no se rechaza \( H_0 \), nunca se puede afirmar que es verdadera.
Errores de Tipo I y II.
-
Error de tipo I: Se comete cuando se decide rechazar la hipótesis nula \( H_0 \) que en realidad es verdadera. La probabilidad de cometer ese error es α.
\( P[Rechazar \hspace{.1cm} H_0 / H_0 \hspace{.1cm} es \hspace{.1cm} cierta]=α \hspace{.1cm}; \hspace{.1cm} 0 \leq α \leq 1 \)
-
Error de tipo II: Se comete cuando se decide no rechazar la hipótesis nula \( H_0 \) que en realidad es falsa. La probabilidad de cometer ese error es β.
\( P[No\hspace{.1cm} rechazar \hspace{.1cm} H_0 / H_0 \hspace{.1cm} es \hspace{.1cm} falsa] =β \hspace{.1cm} ; \hspace{.1cm} 0 \leq β \leq 1 \)
Por tanto,
- 1 – α es la probabilidad de tomar una decisión correcta cuando \( H_0 \) es verdadera.
- 1 – β es la probabilidad de tomar una decisión correcta cuando \( H_0 \) es falsa.
En la tabla siguiente presentamos las decisiones y posibles errores que se pueden cometer
\( \begin{array}{||l|cc||} \hline & \hspace{5cm} Decisión \\ \hline & Rechazar \hspace{.1cm} H_0 & No \hspace{.1cm} rechazar H_0 \\ \hline Hipótesis \hspace{.1cm} cierta \hspace{.1cm} H_0 & \begin{array}{c} Error \hspace{.1cm} de \hspace{.1cm} tipo \hspace{.1cm}I \\ P = α \end{array} & \begin{array}{c} Decisión \hspace{.1cm} correcta \\ P = 1- \beta \end{array} \\ \hline Hipótesis \hspace{.1cm} falsa \hspace{.1cm} H_0 & \begin{array}{c} Decisión \hspace{.1cm} correcta \\ P = 1-\alpha \end{array} & \begin{array}{c} Error \hspace{.1cm} de \hspace{.1cm} tipo \hspace{.1cm}II \\ P = β \end{array} \\ \hline \end{array} \)
Expresión 3: Cuadro tipos de errores
- La dificultad al usar un procedimiento basado en datos muestrales es que debido a la variabilidad de muestreo, puede resultar una muestra no representativa, y por tanto, resultaría un rechazo erróneo de H0.
- La probabilidad de cometer un error de tipo I con nuestra decisión es una probabilidad conocida, pues el valor de α lo fija el propio investigador.
- Sin embargo, la probabilidad de cometer un error de tipo II, β , es un valor desconocido que depende de tres factores:
-
- La hipótesis \( H_1 \) que consideremos verdadera.
- El valor de α .
- El tamaño del error típico (desviación típica) de la distribución muestral utilizada para efectuar el contraste.
-
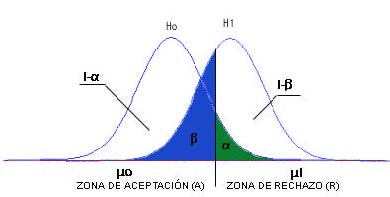 Figura 5: Zonas de rechazo y no rechazo
Figura 5: Zonas de rechazo y no rechazo
Relaciones entre los errores de Tipo I y II. El estudio de las relaciones entre los errores lo realizamos mediante el contraste de hipótesis:
\( \begin{array}{c} H_0 \equiv \mu = \mu_0 \\ H_1 \equiv μ = μ_1 \end{array} \)
Expresión 4: Contraste de hipótesis
Para ello utilizamos la información muestral proporcionada por el estadístico media muestral \( (\overline{X})\)
Cualquier valor atribuido a \( \mu_1 \) en \( H_1\) (siempre mayor a \( \mu_0 \)) generará distribuciones muestrales distintas para la media muestral. Aunque todas tendrán la misma forma, unas estarán más alejadas que otras de la curva de \( H_0 \), es decir, unas serán distintas de otras únicamente en el valor asignado a \( \mu_1 \).
- Cuanto más se aleje el valor \( \mu_1 \) de \( \mu_0 \), más hacia la derecha se desplazará la curva \( H_1 \), y en consecuencia, más pequeña se hará el área \( \beta \). Por lo tanto, el valor de \( \beta \) depende del valor concreto de \( \mu_1 \) que consideremos verdadero dentro de todos los afirmados por \( H_1 \) .
- Cuanto mayor es \( \alpha \), menor es \( \beta \). Se relacionan de forma inversa.
-
Para una distancia dada entre \( \mu_0 \) y \( \mu_1 \), el solapamiento entre las curvas correspondientes a uno y otro parámetro será tanto mayor cuanto mayor sea el error típico de la distribución muestral representada por esas curvas (cuanto mayor es el error típico de una distribución, más ancha es esa distribución). Y cuanto mayor sea el solapamiento, mayor será el valor de \( \beta \).
En lugar de buscar procedimientos libres de error, debemos buscar procedimientos para los que no sea probable que ocurran ningún tipo de estos errores. Esto es, un buen procedimiento es aquel para el que es pequeña la probabilidad de cometer cualquier tipo de error. La elección de un valor particular de corte de la región de rechazo fija las probabilidades de errores tipo I y tipo II.
Debido a que \( H_0 \) especifica un valor único del parámetro, hay un solo valor de \( \alpha \). Sin embargo, hay un valor diferente de \( \beta \) por cada valor del parámetro recogido en \( H_1 \).
En general, un buen contraste o buena regla de decisión debe tender a minimizar los dos tipos de error inherentes a toda decisión. Como \( \alpha \) queda fijado por el investigador, trataremos de elegir una región donde la probabilidad de cometer el error de tipo II sea la menor .
Usualmente, se diseñan los contrastes de tal manera que la probabilidad a sea el 5% (0,05), aunque a veces se usan el 10% (0,1) o 1% (0,01) para adoptar condiciones más relajadas o más estrictas.
Potencia de un contraste.
Es la probabilidad de decidir \( H_1 \) cuando ésta es cierta
\( P[decidir \hspace{.1cm} H_1 / H_1 \hspace{.1cm} es \hspace{.1cm} verdadera]=1- \beta \)
El concepto de potencia se utiliza para medir la bondad de un contraste de hipótesis. Cuanto más lejana se encuentra la hipótesis \( H_1 \) de \( H_0 \) menor es la probabilidad de incurrir en un error tipo II y, por consiguiente, la potencia tomará valores más próximos a 1.
Si la potencia en un contraste es siempre muy próxima a 1 entonces se dice que el estadístico de contraste es muy potente para contrastar \( H_0 \) ya que en ese caso las muestras serán, con alta probabilidad, incompatibles con \( H_0 \) cuando \( H_1 \) sea cierta.
Por tanto puede interpretarse la potencia de un contraste como su sensibilidad o capacidad para detectar una hipótesis alternativa. La potencia de un contraste cuantifica la capacidad del criterio utilizado para rechazar H0 cuando esta hipótesis sea falsa
Es deseable en un contraste de hipótesis que las probabilidades de ambos tipos de error fueran tan pequeñas como fuera posible. Sin embargo, con una muestra de tamaño prefijado, disminuir la probabilidad del error de tipo I, α, conduce a incrementar la probabilidad del error de tipo II, β. El recurso para aumentar la potencia del contraste, esto es, disminuir la probabilidad de error de tipo II, es aumentar el tamaño muestral lo que en la práctica conlleva un incremento de los costes del estudio que se quiere realizar
El concepto de potencia nos permite valorar cual entre dos contrastes con la misma probabilidad de error de tipo I, α, es preferible. Se trata de escoger entre todos los contrastes posibles con α prefijado aquel que tiene mayor potencia, esto es, menor probabilidad β de incurrir en el error de tipo II. En este caso el Lema de Neyman-Pearson garantiza la existencia de un contraste de máxima potencia y determina cómo construirlo.
Potencia de un contraste de hipótesis
Contrastes de hipótesis paramétricos
El propósito de los contrastes de hipótesis es determinar si un valor propuesto (hipotético) para un parámetro u otra característica de la población debe aceptarse como plausible con base en la evidencia muestral.
Podemos considerar las siguientes etapas en la realización de un contraste:
-
-
El investigador formula una hipótesis sobre un parámetro poblacional, por ejemplo que toma un determinado valor
-
Selecciona una muestra de la población
-
Comprueba si los datos están o no de acuerdo con la hipótesis planteada, es decir, compara la observación con la teoría
- Si lo observado es incompatible con lo teórico entonces el investigador puede rechazar la hipótesis planteada y proponer una nueva teoría
- Si lo observado es compatible con lo teórico entonces el investigador puede continuar como si la hipótesis fuera cierta.
-
Contrastes de hipótesis para la media de una población normal
El objetivo es probar uno de los siguientes contrastes de hipótesis con respecto de μ
\( \begin{array}{ccccc} H_0 \equiv \mu = \mu_0 & & H_0 \equiv μ \leq μ_0 & & H_0 \equiv μ \geq μ_0 \\ & o & & o & \\ H_1 \equiv μ \neq μ_0 & & H_1 \equiv μ > μ_0 & & H_1 \equiv μ < μ_0 \end{array} \)
Expresión 5: Tipos de contrastes de hipótesis
donde \( μ_0 \) es un valor conocido dado de antemano. Para ello se toma una m.a.s concreta \( x_1, x_2, \cdots , x_{n} \) cuya media valdrá: \( \bar {x} = \displaystyle \frac{1} {n} \displaystyle \sum_{i=1}^{n} x_{i} \)
Se distinguen dos situaciones: a) Varianza poblacional conocida y b) varianza poblacional desconocida.
Contrastes de hipótesis para la media de una población normal con Varianza conocida
El caso en el que se desea resolver un contraste de hipótesis para la media de una variable continua y, además, se conoce el valor de la varianza de dicha variable en toda las poblaciones es el más sencillo de todos y, a la vez, el menos usual.
Supongamos una muestra aleatoria \( X_1, X_2, \cdots, X_n \) de tamaño n de valores de una variable aleatoria que sigue una distribución normal de media μ desconocida, y de desviación típica σ conocida. Se plantea el siguiente contraste:
\( \begin{array}{c} H_0 \equiv \mu = \mu_0 \\ H_1 \equiv μ \neq μ_0 \end{array} \)
Expresión 6: Contraste de hipótesis bilateral
\( Z= \displaystyle \frac {\overline{X}-μ_0} {σ/ \sqrt{n}} \)
Expresión 7: Estadístico de contraste de la media con varianza conocida
que sigue una distribución normal de media 0 y desviación típica 1 cuando la hipótesis nula es cierta. A continuación se busca el cuantil 1-α/2 de una distribución normal y se comparan ambos valores.
En el contraste de hipótesis bilateral, si el valor absoluto del estadístico de contraste es mayor que el cuantil, se rechazará la hipótesis nula. En caso contrario, no se rechazará.
En el contraste de hipótesis unilateral
- Con hipótesis alternativa del tipo <, el valor crítico \( – z_{1-α} \) y la hipótesis nula se rechaza cuando \( Z < – z_{1- α} \)
- Con hipótesis alternativa del tipo >. el valor crítico \( – z_{1-α} \) y la hipótesis nula se rechaza cuando \( Z > – z_{1- α} \)
R no incluye una función específica para la resolución de contrastes de hipótesis de este tipo. Aun así, pueden resolverse de una forma muy sencilla como se muestra en el siguiente ejemplo.
Supuesto Práctico 1
Consideramos la base de datos empleados.xls que contiene una serie de variables medidas en los empleados de una empresa. A partir de dicha base de datos y suponiendo la normalidad de la variable altura, ¿puede concluirse con un 95% de confianza que la altura media de los empleados es de 185 cm, sabiendo que la varianza poblacional es 6?
Abrimos R-Commander, para ello, en primer lugar nos situamos en R y mediante la instrucción:
> library(Rcmdr)
Se abre la siguiente ventana que corresponde a R-Commander
Figura 6: Ventana de R-Commander
Los datos de Excel, empleados.xls, los importamos a R-Commander mediante el Menú
Datos/Importar datos/desde un archivo de Excel
Figura 7: Datos/Importar datos/desde un archivo de Excel
Pulsamos Editar conjunto de datos o Visualizar conjunto de datos y nos muestra el conjunto de datos
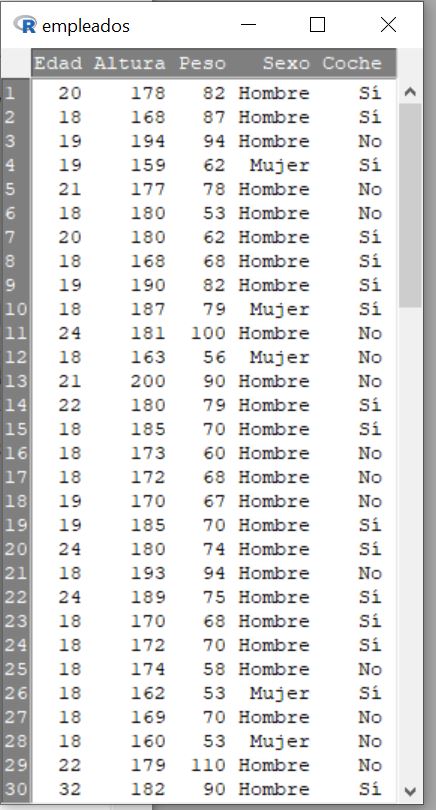
Figura 8: Datos del fichero empleados.xls
Los visualizamos y los guardamos (Datos/Conjunto de datos activo/Guardar el conjunto de datos activo) como fichero empleados.RData.
El contraste de hipótesis asociado a este ejercicio es
\( \begin{array}{c} H_0 \equiv \mu = 185 \\ H_1 \equiv μ \neq 185 \end{array} \)
Expresión 8: Contraste de hipótesis del supuesto práctico 1
En R-Commander no existe ninguna función que nos ayude a resolver este contraste directamente, de manera que debemos calcular el valor del estadístico de contraste y ver si verifica o no la condición de rechazo.
En R-Script escribimos las sentencias
alpha<- 0.05
varianza <- 6
mu0<-185
n <- nrow(empleados)
media <- mean(empleados$Altura)
z0 <- (media – mu0) / (sqrt(varianza) / sqrt(n))
z0
cuantil<-qnorm(1-alpha/2)
cuantil
Las señalizamos todas y pulsamos Ejecutar, se muestra la siguiente salida
> z0
[1] -32.49615
> cuantil
[1] 1.959964
Como \( |Z_0| > Z_{1-\alpha/2} \) rechazamos la hipótesis nula, por lo que la altura de los empleados es distinta de 185.
Contrastes de hipótesis para la media de una población normal con Varianza desconocida
Supongamos que la varianza poblacional de la variable de interés es desconocida. Nuestro objetivo sigue siendo la resolución del contraste de hipótesis para la media de dicha variable.
\( \begin{array}{ccccc} H_0 \equiv \mu = \mu_0 & & H_0 \equiv μ \geq μ_0 & & H_0 \equiv μ \leq μ_0 \\ & o & & o & \\ H_1 \equiv μ \neq μ_0 & & H_1 \equiv μ < μ_0 & & H_1 \equiv μ > μ_0 \end{array} \)
Expresión 9: Tipos de contrastes de hipótesis
Supongamos, de nuevo, una muestra aleatoria \( X_1, X_2, \cdots, X_n \), de tamaño n de valores de la variable aleatoria que sigue una distribución normal de media \( \mu \) y desviación típica \( \sigma \), ambas desconocidas. Para resolver el contraste de hipótesis para \( \mu \) en este caso partimos del estadístico de contraste
\( T= \displaystyle \frac {\overline{X}-μ_0} {s/ \sqrt{n}} \)
Expresión 10: Expresión del estadístico de contraste
dicho estadístico sigue una distribución t de Student con n-1 grados de libertad cuando la hipótesis nula es cierta. En la fórmula anterior, s hace referencia a la cuasidesviación típica muestral.
Fijado un nivel de significación α
a) Para la hipótesis alternativa \( H_1: \mu \neq \mu_0 \) la correspondiente región de no rechazo es \( (-t_{α/2;n-1}, t_{α/2;n-1}) \) y el estadístico de contraste adopta la forma de la Expresión 10
y se utiliza la siguiente regla de decisión
\( \begin{array}{ccccc} H_0 \equiv \mu = \mu_0 & Si & t_ {exp} < t_{α/2;n-1} & \Rightarrow & No \hspace{.2cm} se \hspace{.2cm} rechaza \hspace{.2cm} H_0 \\ H_1 \equiv μ \neq μ_0 & Si & t_ {exp} \geq t_{α/2;n-1} & \Rightarrow & Se \hspace{.2cm} rechaza \hspace{.2cm} H_0 \end{array} \)
Expresión 11: Contraste para \( H_1 \equiv \mu \neq \mu_0 \) y regla de decisión
b) Para la hipótesis alternativa \( H_1 \equiv \mu > \mu_0 \) la correspondiente región de no rechazo es \( ( -\infty, t_{\alpha;n-1}) \) y el estadístico de contraste es el mismo que en a). Se utiliza la siguiente regla de decisión
\( \begin{array}{ccccc} H_0 \equiv \mu \leq \mu_0 & Si & t_ {exp} < t_{α;n-1} & \Rightarrow & No \hspace{.2cm} se \hspace{.2cm} rechaza \hspace{.2cm} H_0 \\ H_1 \equiv μ > μ_0 & Si & t_ {exp} \geq t_{α;n-1} & \Rightarrow & Se \hspace{.2cm} rechaza \hspace{.2cm} H_0 \end{array} \)
Expresión 12: Contraste para \( H_1 \equiv μ > μ_0 \) y regla de decisión
c) Para la hipótesis alternativa \( H_1 \equiv μ < μ_0 \) la correspondiente región de no rechazo es \( (- t_{\alpha;n-1}, \infty,) \), el estadístico de contrate es el anterior y se adopta la siguiente regla de decisión
\( \begin{array}{ccccc} H_0 \equiv \mu \geq \mu_0 & Si & t_ {exp} > – t_{α;n-1} & \Rightarrow & No \hspace{.2cm} se \hspace{.2cm} rechaza \hspace{.2cm} H_0 \\ H_1 \equiv μ < μ_0 & Si & t_ {exp} \leq – t_{α;n-1} & \Rightarrow & Se \hspace{.2cm} rechaza \hspace{.2cm} H_0 \end{array} \)
Expresión 13: Contraste para \( H_1 \equiv \mu < \mu_0 \) y regla de decisión
Supuesto Práctico 2
Considerando el conjunto de datos de empleados y asumiendo que la variable que mide la edad de los empleados sigue una distribución normal con varianza desconocida, contrastar con un nivel de significación del 10% si la edad media poblacional puede considerarse igual a 25 años frente a que esta edad es menor.
En primer lugar, planteamos el contraste de hipótesis asociado a este supuesto
\( \begin{array}{c} H_0 \equiv \mu = 25 \\ H_1 \equiv μ < 25 \end{array} \)
Expresión 14: Contraste de hipótesis del supuesto práctico 2
Para calcular un contraste de hipótesis para la media de una población normal con varianza desconocida mediante R-Commander, elegimos la opción
Estadísticos/ Medias/ Test t para una muestra
Figura 9: Estadísticos/ Medias/ Test t para una muestra
Se mostrará el siguiente cuadro de diálogo
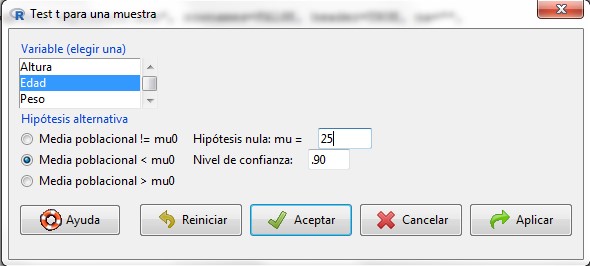
Figura 10: Test t para una muestra
- Elegimos una variable, que debe ser aquella cuya media estemos contrastando.
- Indicamos cuál es la hipótesis alternativa que vamos a contrastar.
- Especificamos el valor con el que estamos comparando la media.
- Especificamos el nivel de confianza, que se calcula como 1 – nivel de significación (en tanto por uno).
- Pulsamos Aceptar
y se muestra la siguiente salida
One Sample t-test
data: Edad
t = -10.718, df = 98, p-value < 2.2e-16
alternative hypothesis: true mean is less than 25
90 percent confidence interval:
-Inf 21.05504
sample estimates:
mean of x
20.51515
Entre los resultados que proporciona R-Commander encontramos, por ejemplo, el valor del estadístico de contraste (t = -10.718). Pero en este caso, la resolución del contraste se hará basándonos en el p-valor (p-value = < 2.2e-16)
El p-valor es una probabilidad (oscila, por lo tanto, entre 0 y 1).
- Si el p-valor es mayor que el nivel de significación, no rechazamos la hipótesis
- Si el p-valor es menor que el nivel de significación, rechazamos la hipótesis nula en favor de la hipótesis alternativa
En nuestro caso, el p-valor vale < 2.2e-16. El nivel de significación es α = 0,10. Como 2.2e-16 < 0,10, rechazamos la hipótesis nula, por lo que podemos considerar que la edad media de los empleados es menor de 25 años.
Contrastes de hipótesis para la diferencias de medias de dos poblaciones normales e independientes
De un modo general, dos muestras se dice que son independientes cuando las observaciones de una de ellas no condicionan para nada a las observaciones de la otra, siendo dependientes en caso contrario. En realidad, el tipo de dependencia que se considera a estos efectos es muy especial: cada dato de una muestra tiene un homónimo en la otra, con el que está relacionada, de ahí el nombre alternativo de muestras apareadas. Por ejemplo, supongamos que se quiere estudiar el efecto de un medicamento, sobre la hipertensión, a un grupo de 20 individuos. El experimento se podría planificar de dos formas:
-
Aplicando el medicamento a 10 de estos individuos y dejando sin tratamiento al resto. Transcurrido un tiempo se miden las presiones sanguíneas de ambos grupos y se contrasta la hipótesis \( H_0: \mu_1 = \mu_2 \hspace{.2cm} vs \hspace{.2cm} H_1: \mu_1 \neq \mu_2 \) para evaluar si las medias son iguales o no. Como las muestras están formadas por individuos distintos sin relación entre sí, se dirá que son muestras independientes.
-
Aplicando el medicamento a los 20 individuos disponibles y anotando su presión sanguínea antes y después de la administración del mismo. En este caso los datos vienen dados por parejas, presión antes y después y tales datos están relacionados entre sí. Las muestras son apareadas.
Consideramos ahora dos variables aleatorias independientes \( X_1 \) y \( X_2 \) con distribuciones Normales de parámetro \( (\mu_1, \sigma_1) \) y \( (\mu_2, \sigma_2) \) respectivamente, de las que vamos a tomar muestras aleatorias independientes de tamaños \( n_1 \) y \( n_2 \), respectivamente.
Nuestro objetivo, en este caso, es resolver un contraste de hipótesis para la diferencia de las medias de ambas distribuciones, es decir, para \( \mu_1 \) y \( \mu_2 \). Este contraste presentará alguna de las formas que se muestran a continuación
\( \begin{array}{ccccc} H_0 \equiv \mu_1 – \mu_2 = d_0 & & H_0 \equiv \mu_1 – \mu_2 \geq d_0 & & H_0 \equiv \mu_1 – \mu_2 \leq d_0 \\ & o & & o & \\ H_1 \equiv \mu_1 – \mu_2 \neq d_0 & & H_1 \equiv \mu_1 – \mu_2 < d_0 & & H_1 \equiv \mu_1 – \mu_2 > d_0 \end{array} \)
Expresión 15: Contraste de hipótesis para la diferencia de medias
En R-Commander, el contraste de las diferencias de medias se resuelve accediendo al menú
Estadísticos / Medias / Test t para muestras independientes
Pero antes de la resolución del contraste, debemos determinar si las varianzas de ambas distribuciones o, equivalentemente, sus desviaciones típicas, \( \sigma_1 \) y \( \sigma_2 \), aun siendo desconocidas, pueden asumirse iguales o no. La resolución del contraste de hipótesis sobre las medias se realiza de forma diferente dependiendo de las varianzas.
Para decidir si las varianzas de las dos distribuciones pueden asumirse iguales o no plantearemos y resolveremos el siguiente contraste de hipótesis:
\( \begin{array}{c} H_0 \equiv \sigma_{1}^{2} = \sigma_{2}^{2} \\ H_1 \equiv \sigma_{1}^{2} \neq \sigma_{2}^{2} \end{array} \)
Expresión 16: Contraste de hipótesis para la igualdad de varianzas
O equivalentemente
\( \begin{array}{c} H_0 \equiv \displaystyle \frac{ \sigma_{1}^{2}} { \sigma_{2}^{2}} = 1 \\ H_1 \equiv \displaystyle \frac {\sigma_{1}^{2} } { \sigma_{2}^{2}} \neq 1 \end{array} \)
Expresión 17: Contraste de hipótesis para la igualdad de varianzas
Para resolver este contraste, partimos del estadístico de contraste
\( F= \displaystyle \frac {s_{1}^{2}} {s_{2}^{2}} \)
Expresión 18: Estadístico de contraste para comparar dos varianzas de dos distribuciones normales e independientes
que sigue una distribución F de Snedecor con \( n_1-1 \) grados de libertad en el numerador y \( n_2-1 \) grados de libertad en el denominador cuando la hipótesis nula del contraste es cierta. Los valores \( s_{1}^{2} \) y \( s_{2}^{2} \) en la expresión anterior hacen referencia a las cuasivarianzas muestrales de la variable en el primer y el segundo grupo, respectivamente.
En R-Commander, el contraste del cociente de varianzas se resuelve accediendo al menú
Estadísticos/ Varianzas/ Test F para dos varianzas
Nota: Tener en cuenta que R-Commander realiza el contraste de hipótesis para la primera categoría de la variable. Para R-Commander la primera categoría de una variable es la que primero aparece siguiendo el orden alfabético, en caso de que las categorías vengan dadas por cadenas de caracteres, o aquella con el número más bajo, en caso de que las categorías se identifiquen mediante un código numérico.
Supuesto Práctico 3
Continuando con los datos relativos a los empleados y asumiendo que el peso en hombres y el peso en mujeres se distribuyen según distribuciones normales con medias y varianzas desconocidas. Contrastar si el peso en ambas poblaciones puede considerarse igual con un nivel de confianza del 95%
Solución
En primer lugar vamos a realizar el contraste sobre la igualdad de varianzas
\( \begin{array}{c} H_0 \equiv \sigma_{hombre}^{2} = \sigma_{mujer}^{2} \\ H_1 \equiv \sigma_{hombre}^{2} \neq \sigma_{mujer}^{2} \end{array} \)
Resolvemos el contraste de hipótesis sobre las varianzas con R-Commander mediante el menú:
Estadísticos / Varianzas / Test F para dos varianzas
Figura 11: Estadísticos / Varianzas / Test F para dos varianzas
Se muestra la siguiente pantalla
Figura 12: Submenú Datos
Submenú Datos: En el cuadro de la izquierda seleccionamos la variable que establece los grupos, Sexo, mientras que en el cuadro de la derecha elegimos la variable cuya varianza queremos contrastar en ambos grupos, Peso.
Pulsamos la pestaña Opciones
Figura 13: Submenú Opciones
Submenú Opciones: Indicamos la forma de la hipótesis nula (en el contraste de varianzas será siempre bilateral) y el nivel de confianza en base al cual se calcularán los resultados.
Pulsamos Aceptar y se muestra la siguiente salida
> Tapply(Peso ~ Sexo, var, na.action=na.omit, data=empleados) # variances by group
Hombre Mujer
166.99626 92.06061
> var.test(Peso ~ Sexo, alternative=’two.sided’, conf.level=.95, data=empleados)
F test to compare two variances
data: Peso by Sexo
F = 1.814, num df = 86, denom df = 11, p-value = 0.2752
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.6112226 3.8937784
sample estimates:
ratio of variances
1.813982
La primera parte de los resultados incluye el valor del estadístico de contraste junto con los grados de libertad del numerador y del denominador. Justo a continuación se muestra el p-valor asociado al contraste. Teniendo en cuenta la significación que se ha fijado para este contraste (el 5%), rechazaremos la hipótesis nula a favor de la alternativa cuando el p-valor sea menor que 0.05. En caso contrario, no contaríamos con evidencia muestral para el rechazo de tal hipótesis nula.
En este Supuesto se verifica que p-valor = 0.2752 > 0,05 = α, por lo que no rechazaríamos la hipótesis nula del contraste, lo que equivale a decir que la varianza de la variable peso puede suponerse igual en los dos grupos.
Una vez contrastada la igualdad de varianzas, resolveremos el contraste sobre la igualdad de medias.
\( \begin{array}{c} H_0 \equiv \mu_{hombre} = \mu_{mujer} \\ H_1 \equiv \mu_{hombre} \neq \mu_{mujer} \end{array} \)
Para ello, debemos acceder al menú
Estadísticos / Medias / Test t para muestras independientes
Figura 14: Estadísticos / Medias / Test t para muestras independientes
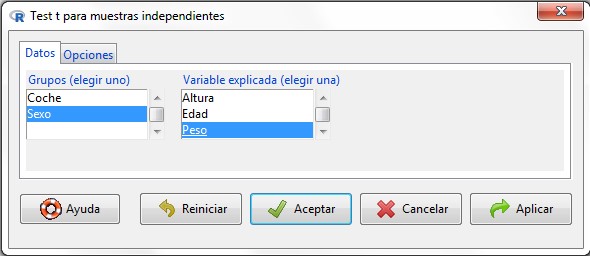
Figura 15: Submenú Datos
Submenú Datos: En el cuadro de la izquierda seleccionamos la variable que establece los grupos, Sexo, mientras que en el cuadro de la derecha elegimos la variable cuya media queremos contrastar en ambos grupos, Peso.
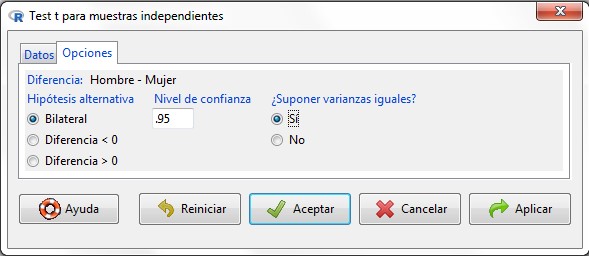
Figura 16: Submenú Opciones
Submenú Opciones: Indicamos la forma de la hipótesis nula y el nivel de confianza en base al cual se calcularán los resultados. El test de igualdad de varianzas que hemos realizado anteriormente nos permite responder a la pregunta sobre si las varianzas pueden asumirse iguales o no. Pulsamos Aceptar
Se muestra la siguiente salida
> t.test(Peso~Sexo, alternative=’two.sided’, conf.level=.95, var.equal=TRUE, data=empleados)
Two Sample t-test
data: Peso by Sexo
t = 3.0597, df = 97, p-value = 0.002865
alternative hypothesis: true difference in means between group Hombre and group Mujer is not equal to 0
95 percent confidence interval:
4.167581 19.556557
sample estimates:
mean in group Hombre mean in group Mujer
76.19540 64.33333
En la primera parte de los resultados se muestra el valor del estadístico de prueba, así como los grados de libertad correspondientes. Como es habitual al realizar un contraste de hipótesis también aparece el p-valor, que para este ejemplo toma el valor 0.002865. Como este p-valor es menor que 0.05 (recordemos que estamos considerando una significación del 5%) rechazamos la hipótesis nula a favor de la alternativa, es decir, el peso medio de hombres y mujeres no puede considerarse igual.
Contrastes de hipótesis para la diferencia de medias de dos poblaciones normales relacionadas
Hasta ahora, hemos considerado que las muestras que se extraen de las dos poblaciones son independientes. En algunas situaciones puede que esto no sea así. Supongamos, por ejemplo, que queremos medir el efecto de un fármaco en un grupo de personas. Para ello, lo lógico es realizar las mediciones oportunas antes y después del suministro del fármaco sobre el mismo grupo de pacientes. Es por ello por lo que las muestras de las dos poblaciones no serán, en ningún caso, independientes. En estos casos, se dice que las muestras son pareadas o están relacionadas y la resolución de contrastes de hipótesis conlleva el uso de técnicas estadísticas distintas a las que se usan cuando las muestras son independientes. Se dice que dos muestras \( X_1, X_2, \cdots, X_n \) e \( Y_1, Y_2, \cdots, Y_n \) están relacionadas o apareadas cuando los datos de las muestras vienen por parejas, uno de cada una de ellas, de manera que cada individuo proporciona dos observaciones.
Sean \( X_1, X_2, \cdots, X_n \) e \( Y_1, Y_2, \cdots, Y_n \) dos muestras aleatorias de tamaño n y relacionadas, de tal forma que la primera procede de una población \( N ( \mu_1, \sigma_1) \) y la segunda de una población \( N ( \mu_2, \sigma_2) \).
El contraste que debemos resolver será alguno de los siguientes:
\( \left \{ \begin{array}{c} H_0 \equiv \mu_1 – \mu_2 = d_0 \\ H_1 \equiv μ_1 – μ_2 \neq d_0 \end{array}\right. \) \( \hspace {2cm} \left \{ \begin{array}{c} H_0 \equiv \mu_1 – \mu_2 \geq d_0 \\ H_1 \equiv μ_1 – μ_2 < d_0 \end{array}\right. \) \( \hspace {2cm} \left \{ \begin{array}{c} H_0 \equiv \mu_1 – \mu_2 \leq d_0 \\ H_1 \equiv μ_1 – μ_2 > d_0 \end{array}\right. \)
Expresión 19: Contraste de hipótesis para la diferencia de medias dos poblaciones normales relacionadas
Supuesto Práctico 4
Se desea evaluar la eficacia de un fármaco para la reducción del nivel de glucosa en los empleados de una fábrica. Para ello, se selecciona una muestra de 10 empleados a los que se les mide su nivel de glucosa en sangre antes y después del suministro del medicamento. Los resultados aparecen recogidos en la siguiente tabla:
\( \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline Antes & 100 & 75.5 & 86 & 95 & 140 & 125 & 149 & 130 & 140 & 105 \\ \hline Después & 102 & 79 & 120 & 100 & 98 & 107 & 115 & 125 & 142 & 120 \\ \hline \end{array} \)
Tabla 1; Datos del Supuesto Práctico 4
¿Puede suponerse, a un nivel de confianza del 90% que el medicamento es eficaz en el sentido de que su ingesta implica una reducción en el nivel medio de glucosa en sangre?
En este caso, nos piden resolver el siguiente contraste de hipótesis:
\( \begin{array}{c} H_0 \equiv \mu_{Glu-An} = \mu_{Glu-Des} \\ H_1 \equiv \mu_{Glu-An} < \mu_{Glu-Des} \end{array} \)
Expresión 20: Contraste de hipótesis del supuesto práctico 4
el cual equivale, claramente, a este otro
\( \begin{array}{c} H_0 \equiv \mu_{Glu-An} – \mu_{Glu-Des} = 0 \\ H_1 \equiv \mu_{Glu-An} – \mu_{Glu-Des} < 0 \end{array} \)
Expresión 21: Contraste de hipótesis del supuesto práctico 4
En primer lugar, debemos crear un nuevo conjunto de datos Datos / Nuevo conjunto de datos con la información que nos proporciona la tabla 1. El conjunto de datos estará formado por dos variables con los niveles de glucosa antes y después de la aplicación del fármaco.
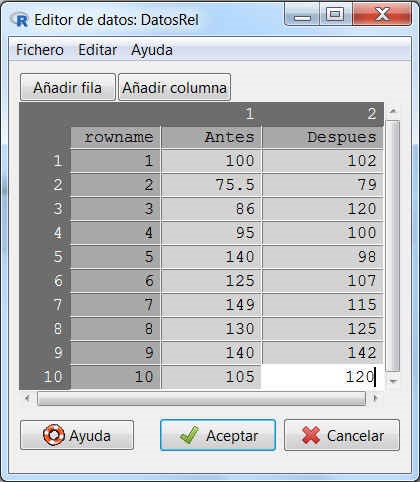
Figura 17: Datos / Nuevo conjunto de datos
Se pulsa Aceptar
En R-Commander, las opciones para resolver un contraste de hipótesis sobre las medias de una variable cuantitativa cuando las muestras están relacionadas se encuentran en Estadísticos / Medias / Test t para datos relacionados.
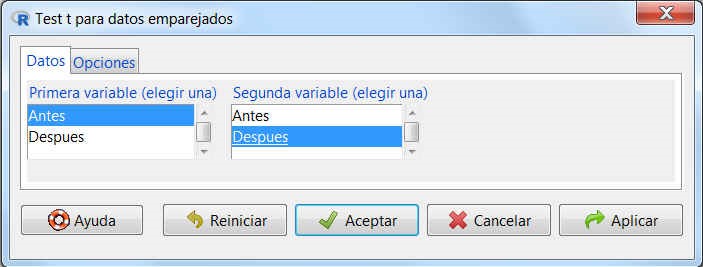
Figura 18: Submenú Datos
En la primera pestaña que aparece, Datos, encontramos dos listas de variables cada una de las cuales incluye todas las variables cuantitativas que son susceptibles de ser analizadas. Seleccionamos en cada lista la variable que nos convenga (Antes y Después en nuestro caso).
Es importante destacar que, a diferencia del caso de muestras independientes, cuando trabajamos con muestras pareadas no necesitamos una variable de agrupación, sino que debemos seleccionar las dos variables a analizar de forma separada.
En la segunda pestaña, Opciones, podemos personalizar el contraste conforme al problema que estemos resolviendo.
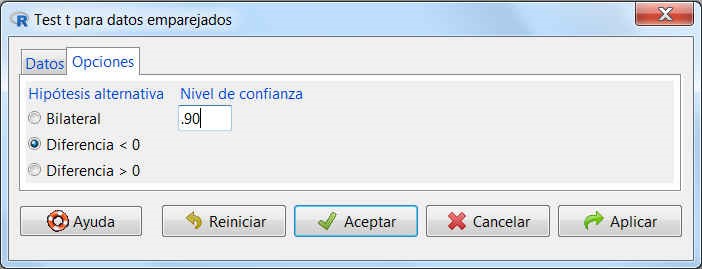
Figura 19: Submenú Opciones
Así, debemos indicar qué forma tiene la hipótesis alternativa: bilateral (hipótesis alternativa de la forma \( \neq \)), de diferencia negativa (hipótesis alternativa de la forma <) o de diferencia positiva (hipótesis alternativa de la forma >). También podemos modificar el nivel de confianza de acuerdo al enunciado del problema.
Si hacemos clic en Aceptar, el programa nos devuelve la siguiente salida:
> with(DatosSup4, (t.test(Antes, Después, alternative=’less’, conf.level=.90, paired=TRUE)))
Paired t-test
data: Antes and Después
t = 0.52714, df = 9, p-value = 0.6946
alternative hypothesis: true difference in means is less than 0
90 percent confidence interval:
-Inf 13.58867
sample estimates:
mean of the differences
3.75
La primera parte de la salida incluye el valor del estadístico de contraste junto con los grados de libertad correspondientes, así como el p-valor asociado. En este caso, dicho p-valor es 0.6946. Dada la significación que se ha fijado para el contraste (10%), rechazaremos la hipótesis nula siempre y cuando el p-valor sea inferior a 0.10. En cualquier otro caso, no contaremos con evidencia para rechazar esta hipótesis nula. Por lo tanto deducimos que los niveles de glucosa son iguales antes y después del tratamiento.
Contrastes de hipótesis para el parámetro p de una distribución Binomial
Supongamos que \( X \) es una variable aleatoria con distribución de probabilidad binomial con parámetro n y π, \( X \rightarrow B(n, π) \), de la que se extrae una muestra aleatoria \( X_1, X_2, \cdots, X_n \) de tamaño n. Sea p la proporción poblacional. Se desea contrastar si el parámetro \( \pi \) puede ser igual a un valor \( \pi_0 \), es decir se desea resolver uno de los siguientes contrastes
\( \begin{array}{|c|c|} \hline Contraste \hspace{.3cm} bilateral & Contrastes \hspace{.3cm} unilaterales \\ \hline H_0 \equiv \pi = \pi_0 & H_0 \equiv \pi \geq \pi_0 \hspace {2cm} H_0 \equiv \pi \leq \pi_0 \\ H_1 \equiv \pi \neq \pi_0 & H_1 \equiv \pi < \pi_0 \hspace {2cm} H_1 \equiv \pi > \pi_0 \\ \hline \end{array} \)
Expresión 22: Tipos de contrastes de hipótesis para la proporción
El contraste de hipótesis para el parámetro p (proporción de éxitos) de una distribución Binomial se basa en la distribución del estadístico muestral π para un tamaño muestral n suficientemente grande.
Denotando por \( \widehat {p} \) la proporción de éxitos de la muestra de una distribución Binomial, se verifica que
\( Z= \displaystyle \frac {\widehat{p}- \pi_0} { \displaystyle \sqrt { \displaystyle \frac { \widehat{p} (1- \widehat {p})} {n}}} \)
Expresión 23: Expresión del estadístico de contraste para el parámetro p de un distribución Binomial
sigue una distribución normal de media 0 y desviación típica 1 bajo la hipótesis nula.
a) Para la hipótesis alternativa \( H_1 \equiv \pi \neq \pi_0 \) la correspondiente región de no rechazo es \( (- z_{α/2}, z_{α/2}) \)
b) Para la hipótesis alternativa \( H_1 \equiv \pi > \pi_0 \) la correspondiente región de no rechazo es \( (-\infty , z_α) \)
c) Para la hipótesis alternativa \( H_1 \equiv \pi < \pi_0 \) la correspondiente región de no rechazo es \( (- z_α , \infty) \).
Supuesto práctico 5
A partir del conjunto de datos de empleados.xls, una empresa de estudios sociales quiere contrastar si la proporción de hombres es superior al 50% con un nivel de confianza al 95%.
En este caso nos piden resolver el siguiente contraste
\( \begin{array}{c} H_0 \equiv \pi_{nombres} = 0.5 \\ H_1 \equiv \pi_{hombres} > 0.5 \end{array} \)
Expresión 24: Contraste de hipótesis del supuesto práctico 5
Respuesta
Recordemos que estamos trabajando con la base de datos empleados.xls que contiene una serie de variables medidas en los empleados de una empresa.
En primer lugar, importamos los datos de Excel a R-Commander mediante el Menú
Datos/Importar datos/desde un archivo de Excel

Pulsamos Aceptar.
Accedemos al menú Test de proporciones para una muestra de R-Commander, seleccionando en el menú principal:
Estadísticos/Proporciones/ Test de proporciones para una muestra.
Figura 20: Estadísticos/Proporciones/ Test de proporciones para una muestra
Figura 21: Submenú Datos
En la primera pestaña del cuadro de diálogo, submenú Datos, que aparece, encontramos una lista con todas las variables cualitativas que pueden utilizarse en este tipo de contrastes, de entre las cuales tenemos que elegir una. Elegimos Sexo
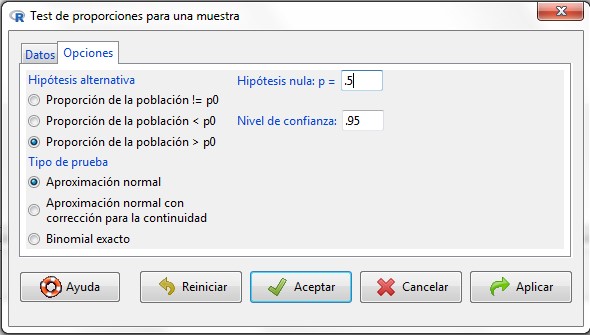
Figura 22: Submenú Opciones
En la pestaña Opciones tenemos que indicar si la hipótesis alternativa de nuestro contraste es del tipo “distinto de” (!=), “menor que” (<) o “mayor que” (>). También introducimos el valor de la proporción que queremos contrastar, que debe coincidir con el valor empleado en la hipótesis nula, y el nivel de confianza. Por último, podemos elegir entre tres tipos de pruebas diferentes, aunque nosotros siempre seleccionaremos la opción por defecto, que se corresponde con la Aproximación normal.
Se muestra la siguiente salida
Frequency counts (test is for first level):
Sexo
Hombre Mujer
87 12
1-sample proportions test without continuity correction
data: rbind(.Table), null probability 0.5
X-squared = 56.818, df = 1, p-value = 2.39e-14
alternative hypothesis: true p is greater than 0.5
95 percent confidence interval:
0.8145345 1.0000000
sample estimates:
p
0.8787879
En primer lugar, se muestra una tabla con las frecuencias absolutas de cada categoría de la variable cualitativa. Es muy importante tener en cuenta que R-Commander realiza el contraste de hipótesis para la primera categoría de la variable. Para R-Commander la primera categoría de una variable es la que primero aparece siguiendo el orden alfabético, en caso de que las categorías vengan dadas por cadenas de caracteres, o aquella con el número más bajo, en caso de que las categorías se identifiquen mediante un código numérico. En este ejemplo, las dos posibles opciones para la variable Sexo son “Hombre” y “Mujer”. Dado que la hipótesis que se ha planteado se ha hecho sobre los hombres no es necesario hacer ninguna modificación. Si, por el contrario, la hipótesis del problema se hubiera planteado sobre las mujeres, deberíamos hacer una recodificación previa de la variable para situar la categoría “Mujer” como la primera.
Con respecto a la salida, el programa nos recuerda que estamos realizando un contraste para una proporción en una población y nos indica el valor de la proporción que se está contrastando (0.5). Justo debajo, se incluye el valor del estadístico de contraste junto con los grados de libertad correspondientes. También aparece el p-valor, el cual nos servirá para resolver el contraste. Para este ejemplo, se tiene un p-valor de 2.39e-14. Como este p-valor es mucho más pequeño que 0.05, que es la significación que se ha prefijado para el contraste, rechazamos la hipótesis nula a favor de la alternativa. Por ello, se puede asumir que la proporción de hombres es mayor a 0.5.
Contrastes de hipótesis para la diferencia de proporciones
Consideremos dos muestras aleatorias \( X_1, X_2, \cdots, X_{n_1} \) e \( Y_1, Y_2, \cdots, Y_{n_2} \) de tamaños \( n_1 \) y \( n_2 \) independientes entre sí, extraídas de poblaciones con distribuciones binomiales \( B (n1, \pi_1) \) y \( B (n2, \pi_2 ) \), respectivamente. Pretendemos resolver alguno de los siguientes contrastes de hipótesis:
\( \left \{ \begin{array}{c} H_0 \equiv \pi_1 – \pi_2 = \delta_0 \\ H_1 \equiv \pi_1 – \pi_2 \neq \delta_0 \end{array}\right. \) \( \hspace {2cm} \left \{ \begin{array}{c} H_0 \equiv \pi_1 – \pi_2 \geq \delta_0 \\ H_1 \equiv \pi_1 – \pi_2 < \delta_0 \end{array}\right. \) \( \hspace {2cm} \left \{ \begin{array}{c} H_0 \equiv \pi_1 – \pi_2 \leq \delta_0 \\ H_1 \equiv \pi_1 – \pi_2 > \delta_0 \end{array}\right. \)
Expresión 25: Contraste de hipótesis para la diferencia de proporciones
Para ello, partimos del estadístico de contraste
\( Z = \displaystyle \frac { (\widehat{p}_1- \widehat{p}_2) – \delta_0} { \displaystyle \sqrt { \displaystyle \frac {\widehat{p}_1(1- \widehat{p}_1) } {n_1} + \displaystyle \frac { \widehat{p}_2 (1- \widehat{p}_2)} {n_2} } } \)
Expresión 26: Estadístico de contraste para la diferencia de proporciones
con \( \widehat{p}_1 \) y \( \widehat{p}_2 \) las proporciones de individuos que presentan la característica de interés en la primera y la segunda muestra, respectivamente. Este estadístico de contraste sigue una distribución normal de media 0 y desviación típica 1 cuando la hipótesis nula del contraste en cuestión es cierta.
Supuesto práctico 6
A partir del conjunto de datos relativo a los empleados, contrastar al 85% si la diferencia de proporciones entre los hombres y mujeres que no tienen coche es la misma.
Respuesta
El contraste que vamos a resolver es
\( \left \{ \begin{array}{c} H_0 \equiv \pi_{hombre \hspace{.1cm} no \hspace{.1cm} coche} = \pi_{mujer \hspace{.1cm} no \hspace{.1cm} coche} \\ H_1 \equiv \pi_{hombre \hspace{.1cm} no \hspace{.1cm} coche} \neq \pi_{mujer \hspace{.1cm} no \hspace{.1cm} coche} \end{array}\right. \)
Expresión 27: Contraste de hipótesis para el Supuesto práctico 7
donde \( \pi_{hombre \hspace{.1cm} no \hspace{.1cm} coche} \) y \( \pi_{mujer \hspace{.1cm} no \hspace{.1cm} coche} \) representan la proporciones de hombres y mujeres que no tienen coche, respectivamente.
Para realizar un contraste de hipótesis para la diferencia de dos proporciones
Estadísticos/ Proporciones/ Test de proporciones para dos muestras
Figura 23: Estadísticos/ Proporciones/ Test de proporciones para dos muestras
Figura 24: Submenú Datos
En la primera pestaña del cuadro de diálogo, submenú Datos, aparecen dos listas con las variables cualitativas que incluye el conjunto de datos. De la primera lista seleccionamos la variable de agrupación, Sexo, y de la segunda, la variable de interés, Coche.
Figura 25: Submenú Opciones
En la segunda pestaña, Submenú Opciones, indicamos la forma de la hipótesis alternativa y el nivel de confianza. En la sección Tipo de prueba dejamos la opción por defecto, Aproximación normal.
Se pulsa Aceptar y se muestra la siguiente salida
Percentage table:
Coche
Sexo No Sí Total Count
Hombre 47.1 52.9 100 87
Mujer 50.0 50.0 100 12
2-sample test for equality of proportions without continuity correction
data: .Table
X-squared = 0.03492, df = 1, p-value = 0.8518
alternative hypothesis: two.sided
85 percent confidence interval:
-0.2503366 0.1928653
sample estimates:
prop 1 prop 2
0.4712644 0.5000000
La salida comienza con una tabla de doble entrada que recoge la información de los porcentajes de cada categoría en cada uno de los dos grupos.
A continuación, encontramos el valor del estadístico de contraste, junto con los grados de libertad correspondientes. También aparece el p-valor, que para este ejemplo es 0.8518. Dado que este p-valor no es inferior al nivel de significación, esto es 0.8518 > 0.15, no podemos rechazar la hipótesis nula del contraste. Por tanto, concluiremos que la proporción de hombres y mujeres que no tienen coche es la misma.
Contrastes de hipótesis no paramétricos
En la sesión anterior hemos estudiado contrastes de hipótesis acerca de parámetros poblacionales, tales como la media y la varianza, de ahí el nombre de contrastes paramétricos. En estadística paramétrica se trabaja bajo el supuesto de que las poblaciones poseen distribuciones conocidas, donde cada función de distribución teórica depende de uno o más parámetros poblacionales. Sin embargo, en muchas situaciones, es imposible especificar la forma de la distribución poblacional. El proceso de obtener conclusiones directamente de las observaciones muestrales, sin formar los supuestos con respecto a la forma matemática de la distribución poblacional se llama teoría no paramétrica.
En esta sesión vamos a realizar procedimientos que no exigen ningún supuesto, o muy pocos acerca de la familia de distribuciones a la que pertenece la población, y cuyas observaciones pueden ser cualitativas o bien se refieren a alguna característica ordenable. En estos casos, cuando no se dispone de información acerca de qué distribución de probabilidad sigue la variable a nivel poblacional, se pueden utilizar técnicas estadísticas no paramétricas para el planteamiento y resolución de contrastes de hipótesis no paramétricos. .Estas técnicas se basan exclusivamente en la información que se recoge en la muestra para resolver los contrastes.
Así, uno de los objetivos de esta sesión es el estudio de contrates de hipótesis para determinar si una población tiene una distribución teórica específica. La técnica que nos introduce a estudiar esas cuestiones se llama Contraste de la Chi-cuadrado para la Bondad de Ajuste. Una variación de este contraste se emplea para resolver los Contrastes de Independencia. Tales contrastes pueden utilizarse para determinar si dos características (por ejemplo preferencia política e ingresos) están relacionadas o son independientes. Y, por último estudiaremos otra variación del contraste de la bondad de ajuste llamado Contraste de Homogeneidad. Tal contraste se utiliza para estudiar si diferentes poblaciones, son similares (u homogéneas) con respecto a alguna característica. Por ejemplo, queremos saber si las proporciones de votantes que favorecen al candidato A, al candidato B o los que se abstuvieron son las mismas en dos ciudades.
El procedimiento Prueba de la Chi-cuadrado
Hemos agrupado los procedimientos en los que el denominador común a todos ellos es que su tratamiento estadístico se aborda mediante la distribución Chi-cuadrado. El procedimiento Prueba de Chi-cuadrado tabula una variable en categorías y calcula un estadístico de Chi-cuadrado. Esta prueba compara las frecuencias observadas y esperadas en cada categoría para contrastar si todas las categorías contienen la misma proporción de valores o si cada categoría contiene una proporción de valores especificada por el usuario.
Contraste de hipótesis no paramétrico para la independencia de los valores de una variable cualitativa
Supongamos que se dispone de información sobre una variable cualitativa, \( X \), y se quiere comprobar si todas las categorías de la variable aparecen por igual. Es decir, se pretende comprobar si las categorías de la variable son independientes o no. El contraste de hipótesis que se debe resolver es el siguiente:
\( H_0 \equiv \) Las categorías de la variable \( X \) aparecen igual
\( H_1 \equiv \) Las categorías de la variable \( X \) no aparecen igual
Para resolver este contraste en R-Commander se utiliza la opción Test Chi-Cuadrado de bondad de ajunte (solo para una variable), que encontramos en Estadísticos /Resúmenes/Distribución de frecuencias.
Supuesto Práctico 7
La directora de un hospital quiere comprobar si los ingresos en el hospital se producen en la misma proporción durante todos los días de la semana. Para ello, se anota el número de ingresos durante una semana cualquiera. Los datos se recogen en la siguiente tabla:
\( \begin{array}{||c|c||} \hline Día \hspace{.1cm} de \hspace{.1cm} la \hspace{.1cm} semana & Número \hspace{.1cm} de \hspace{.1cm} ingresos \\ \hline Lunes & 78 \\ \hline Martes & 90 \\ \hline Miércoles & 94 \\ \hline Jueves & 89 \\ \hline Viernes & 110 \\ \hline Sábado & 84 \\ \hline Domingo & 44 \\ \hline \end{array} \)
Tabla 2: Datos del Supuesto Práctico 7
Contrastar, a un nivel de significación del 5%, si la hipótesis de la directora del hospital puede suponerse cierta. ¿Puede asumirse que las proporciones de ingresos de lunes a domingo son (0.15, 0.15, 0.15, 0.15, 0.20, 0.15, 0.05)?
Solución
En primer lugar, que tenemos que abrir R-Commander, para ello, nos situamos en R y escribimos la siguiente instrucción:
> library(Rcmdr)
Una vez situados en R-Commander, introducimos los datos. Para ello, creamos un fichero de texto como se muestra en la Imagen

Tabla 3: Datos del Supuesto Práctico 7 (.txt)
Como puede verse, en la primera fila introducimos el nombre de las variables entre comillas y separados por un espacio. A continuación, en las siguientes filas se van introduciendo los datos que aparecen en la tabla. Hay que tener en cuenta que las modalidades de las variables cualitativas hay que escribirlas entre comillas.
A continuación, cargamos el fichero seleccionando:
Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra la siguiente ventana
en la cual vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Ingresos. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Pulsamos Aceptar y se muestra una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

Si pulsamos Visualizar conjunto de datos se muestra la siguiente pantalla
Para transformar la tabla de frecuencias en un conjunto de datos (data.frame) con el que R-Commander pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script
P<-rep(Ejemplo_Ingresos$Dias,Ejemplo_Ingresos$frecuencias)
Dias<-data.frame(P)
Seleccionamos ambas instrucciones y pulsamos Ejecutar
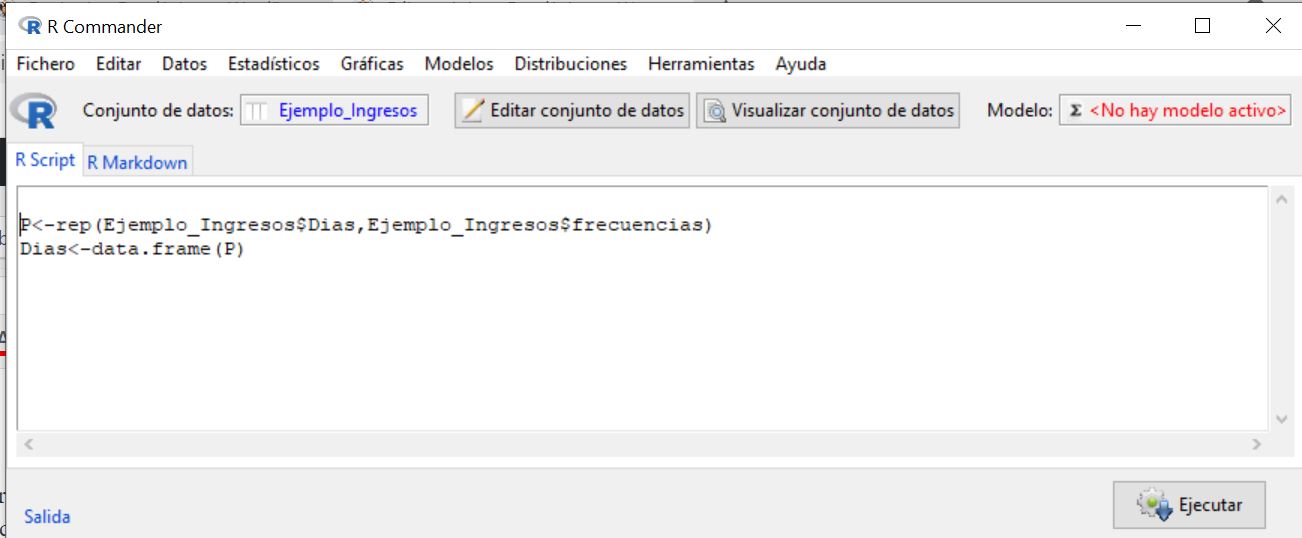
Para visualizar el conjunto de datos en forma de lista deberemos pulsar en el botón Conjunto de datos y seleccionar el nuevo conjunto de datos creado en forma de lista, al que hemos llamado Dias y pulsamos Aceptar.
 Una vez seleccionado, si pulsamos en el botón Visualizar conjunto de datos podemos comprobar que la tabla de frecuencias se ha transformado en un listado de datos:
Una vez seleccionado, si pulsamos en el botón Visualizar conjunto de datos podemos comprobar que la tabla de frecuencias se ha transformado en un listado de datos:
El contraste que se debe resolver es:
\( H_0 \equiv \) Los ingresos en el hospital se producen en la misma proporción todos los días de la semana
\( H_1 \equiv \) Los ingresos en el hospital no se producen en la misma proporción todos los días de la semana
Para resolver este contraste seleccionamos en el menú: Estadísticos/ Resúmenes/Distribución de frecuencias
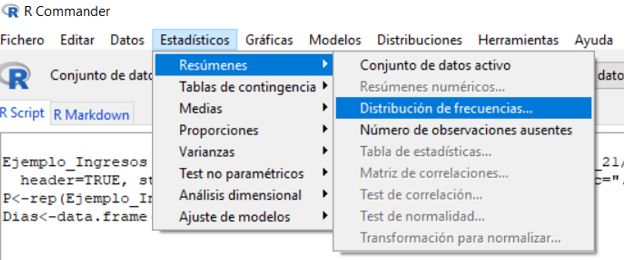
Se muestra la siguiente ventana
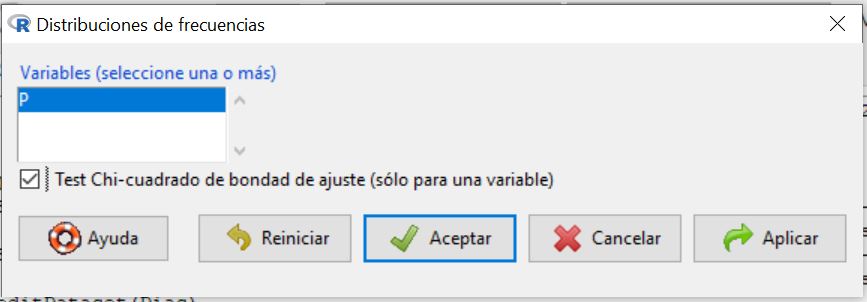
en la que tenemos que seleccionar la variable en estudio, clickar en Test Chi-Cuadrado de bondad de ajuste y pulsar Aceptar.
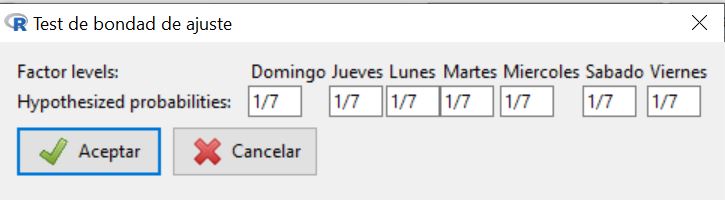
El siguiente paso es introducir las proporciones que queremos contrastar. Por defecto, aparece la misma proporción para todos los días de la semana y, como en este caso es lo que queremos comprobar (ver \( H_0 \)), pulsamos Aceptar sin modificar nada.
En la ventana de resultados nos aparece la siguiente información:
- En primer lugar, las frecuencias absolutas de los ingresos para cada día de la semana.
- A continuación, se no proporcionan los porcentajes de ingresos por día.
- Para finalizar se muestra el estadístico de contraste del Test Chi-Cuadrado (X-squared), los grados de libertad de la distribución Chi-Cuadrado para este ejemplo (df) y, por último, el p-valor asociado al contraste (p-value).
counts:
P
Domingo Jueves Lunes Martes Miercoles Sabado Viernes
44 89 78 90 94 84 110
percentages:
P
Domingo Jueves Lunes Martes Miercoles Sabado Viernes
7.47 15.11 13.24 15.28 15.96 14.26 18.68
Chi-squared test for given probabilities
data: .Table
X-squared = 29.389, df = 6, p-value = 0.00005135
El estadístico de contraste, que sigue una distribución chi-cuadrado, toma el valor 29.389. Los grados de libertad de la distribución chi-cuadrado para este ejemplo son 6. El p-valor asociado al contraste es menor que 0.05 por lo que, considerando un nivel de significación del 5%, se rechaza la hipótesis nula. Es decir, se concluye que los ingresos hospitalarios no se producen en la misma proporción todos los días de la semana.
Para comprobar si podemos asumir que las proporciones de ingresos correspondientes a cada día de la semana (de Lunes a Domingo) son (0.15, 0.15, 0.15, 0.15, 0.20, 0.15, 0.05), seguimos los mismos pasos, pero teniendo en cuenta que, ahora, tenemos que introducir los valores de las nuevas proporciones consideradas y que R-Commander ordena los días de la semana alfabéticamente y no en el orden en el que nos los da el enunciado del problema.

En la ventana de salida aparecen los nuevos resultados:
counts:
P
Domingo Jueves Lunes Martes Miercoles Sabado Viernes
44 89 78 90 94 84 110
percentages:
P
Domingo Jueves Lunes Martes Miercoles Sabado Viernes
7.47 15.11 13.24 15.28 15.96 14.26 18.68
Chi-squared test for given probabilities
data: .Table
X-squared = 9.5286, df = 6, p-value = 0.146
En este caso, el valor del estadístico de contraste es 9.5286. El p-valor asociado es 0.146 que, al ser superior a 0.05, nos indica que no se puede rechazar la hipótesis nula. Esto equivale a decir que, a un nivel de significación del 5%, puede suponerse que los ingresos hospitalarios se producen según los valores de las proporciones consideradas.
Supuesto Práctico 8
Lanzamos un dado 720 veces y obtenemos los resultados que se muestran en la tabla.
\( \begin{array}{||c|c|c|c|c|c|c||} \hline x_i & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline n_i & 116 & 120 & 115 & 120 & 125 & 124 \\ \hline \end{array} \)
Tabla 4: Datos del Supuesto Práctico 8
Contrastar la hipótesis de que el dado está bien construido.
Solución
En primer lugar vamos a introducir los datos en R-Commander. Para ello, creamos un fichero de texto como el que aparece en la Imagen

Tabla 5: Datos del Supuesto Práctico 8 (.txt)
Como puede verse, en la primera fila introducimos el nombre de las variables entre comillas y separados por un espacio. A continuación, en las siguientes filas se van introduciendo los datos que aparecen en la tabla. Hay que tener en cuenta que las modalidades de las variables cualitativas hay que escribirlas entre comillas. No obstante, al introducir valores numéricos R-Commander toma la variable “Resultado” como cuantitativa. Para solucionar esto, tendremos que convertir esta variable en factor.
En primer lugar, cargamos el fichero creado:
Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Nos muestra la siguiente ventana, en la cual vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Dado. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Pulsamos Aceptar y se muestra una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos comprobar que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

A continuación, convertimos la variable “Resultado” en cualitativa mediante la opción
Datos/Modificar variables del conjunto de datos activo/Convertir variable numérica en factor
Se muestra la siguiente ventana
 en la que seleccionamos la variable que queremos convertir (Resultado) y nos da la opción de asignarle nombres a los distintos valores de la variable. En nuestro caso, vamos a utilizar los números, por tanto seleccionamos esta opción y pulsamos Aceptar.
en la que seleccionamos la variable que queremos convertir (Resultado) y nos da la opción de asignarle nombres a los distintos valores de la variable. En nuestro caso, vamos a utilizar los números, por tanto seleccionamos esta opción y pulsamos Aceptar.
Cuando aceptamos, se muestra la siguiente ventana
R-Commander nos dice que la variable “Resultado” ya existe y nos pregunta si queremos sobrescribirla. Le decimos que Si.
Para transformar la tabla de frecuencias en un conjunto de datos (data.frame) con el que R-Commander pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script, seleccionar ambas a la vez y pulsamos Ejecutar
P<-rep(Ejemplo_Dado$Resultado,Ejemplo_Dado$Frecuencia)
Resultados<-data.frame(P)
El nuevo conjunto de datos creado en forma de lista lo hemos llamado Resultados, y es el que tenemos que seleccionar en la pestaña de Conjunto de datos.
Y se muestra en el Conjunto de datos

Que el dado esté bien construido equivale a decir que todos sus valores aparecen en la misma proporción. Por tanto, el contraste de hipótesis que se debe resolver es el siguiente:
\( H_0 \equiv \) Los valores del dado aparecen en la misma proporción
\( H_1 \equiv \) Los valores del dado no aparecen en la misma proporción
Para ello, en el menú seleccionamos: Estadísticos/ Resúmenes/Distribución de frecuencias y se muestra la siguiente ventana en la que tenemos que seleccionar la variable en estudio (P), clickar en Test Chi-Cuadrado de bondad de ajuste.. y pulsar Aceptar.
El siguiente paso es introducir las proporciones que queremos contrastar. Por defecto, aparece la misma proporción para todos los posibles resultados del dado y, como en este caso, es lo que queremos comprobar (ver \( H_0 \)), pulsamos Aceptar sin modificar nada.
counts:
P
1 2 3 4 5 6
116 120 115 120 125 124
percentages:
P
1 2 3 4 5 6
16.11 16.67 15.97 16.67 17.36 17.22
Chi-squared test for given probabilities
data: .Table
X-squared = 0.68333, df = 5, p-value = 0.9839
La ventana de resultados muestra que el estadístico de contraste, que sigue una distribución Chi-cuadrado, toma el valor 0.68333. Los grados de libertad de la distribución Chi-cuadrado para este ejemplo son 5. El p-valor asociado al contraste es igual a 0.9839, mayor que 0.05 por lo que, considerando un nivel de significación del 5%, no podemos rechazar la hipótesis nula. Es decir, todos los valores del dado aparecen en la misma proporción. Dicho de otra forma, el dado está bien construido.
Contraste de hipótesis no paramétricos para la independencia de dos variables cualitativas
Supongamos que se dispone de datos de dos variables cualitativas, X e Y, y se quiere comprobar si los valores que toma una de ellas dependen en cierta medida de los valores que toma la otra. En tal caso, se dice que las variables X e Y son dependientes. Para comprobar la dependencia (o, equivalentemente, la independencia) de X e Y se debe resolver el siguiente contraste de hipótesis
\( H_0 \equiv \) X e Y son variables independientes
\( H_1 \equiv \) X e Y no son variables independientes (son dependientes)
Para resolver este contraste en R-Commander se utiliza la opción Test de independencia Chi-Cuadrado, que encontramos en Estadísticos/Tablas de contingencia/Tabla de doble entrada.
Supuesto Práctico 9
La siguiente tabla muestra información sobre el número de ejemplares de 7 especies de peces avistados aguas arriba y aguas abajo en un río.
\( \begin{array}{||c|cc||} \hline & \hspace{3cm} Zona & \\ \hline & Aguas \hspace{.1cm} arriba & Aguas \hspace{.1cm} abajo \\ \hline EspecieA & 37 & 19 \\ \hline EspecieB & 12 & 10 \\ \hline Especie C & 10 & 7 \\ \hline EspecieD & 18 & 20 \\ \hline Especie E & 11 & 8 \\ \hline Especie F & 16 & 12 \\ \hline EspecieG & 59 & 24 \\ \hline \end{array} \)
Tabla 6: Datos del Supuesto Práctico 10
Contrastar, a un nivel de significación del 5%, si la especie de pez y la zona de avistamiento pueden considerarse variables independientes.
Solución
En primer lugar, introduzcamos en R-Commander los datos que proporciona el enunciado. Para ello, creamos un fichero de texto como el que aparece en la Imagen

Tabla 7: Datos del supuesto práctico 9
Como puede verse, en la primera fila introducimos el nombre de las variables entre comillas y separados por un espacio. A continuación, en las siguientes filas se van introduciendo los datos que aparecen en la tabla. Hay que tener en cuenta que las modalidades de las variables cualitativas hay que escribirlas entre comillas.
A continuación, cargamos el fichero seleccionando en el menú principal: Datos/Importar datos/desde archivo de texto, portapapeles o URL… y se muestra la siguiente salida
En esta ventana introducimos el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Peces. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas. Pulsamos Aceptar y se muestra una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

Para transformar la tabla de contingencia en un conjunto de datos (data.frame) con el que R-Commander pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script, seleccionar las tres instrucciones a la vez y darle a Ejecutar:
P<-rep(Ejemplo_Peces$Especie,Ejemplo_Peces$Frecuencia)
Q<-rep(Ejemplo_Peces$Zona,Ejemplo_Peces$Frecuencia)
Especie_Zona<-data.frame(P,Q)
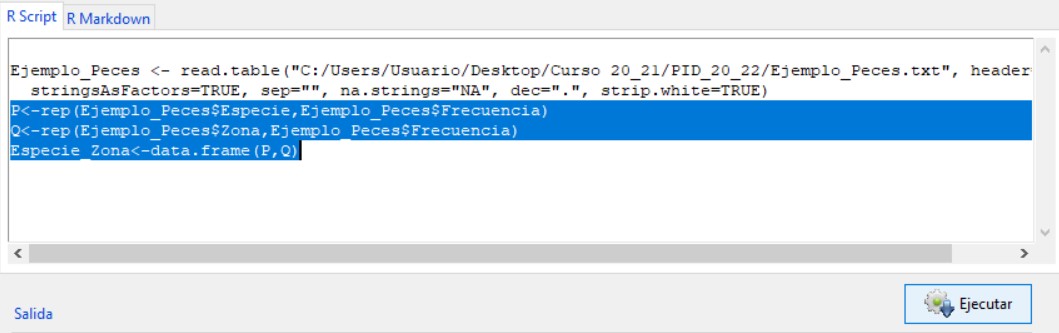
Para visualizar el conjunto de datos en forma de lista deberemos pulsar en el botón Conjunto de datos y seleccionar el nuevo conjunto de datos creado, al que hemos llamado Especie_Zona (observar la tercera instrucción).
Pulsamos Aceptar y se muestra

Pulsando el botón Visualizar conjunto de datos podemos comprobar que la tabla de frecuencias se ha transformado en un listado de datos:
El contraste de hipótesis que se debe resolver es:
\( H_0 \equiv \) La especie y la zona de avistamiento son independientes
\( H_1 \equiv \) La especie y la zona de avistamiento no son independientes
Para ello, en el menú seleccionamos las opciones: Estadísticos/Tablas de contingencia/Tabla de doble entrada
Se muestra la siguiente ventana

En esta ventana, si nos fijamos en la esquina superior izquierda, tenemos dos pestañas. En la pestaña Datos tenemos que seleccionar las variables que queremos que aparezcan tanto por filas (en nuestro caso, la variable P a la que hemos asignado el tipo de Especie) como por columnas (seleccionamos la variable Q a la que hemos asignado la Zona).

En la pestaña Estadísticos tenemos la opción de incluir algún porcentaje en la tabla de doble entrada, aunque por defecto aparece sin porcentajes. En principio, lo vamos a dejar así. También aparece seleccionado el Test de independencia Chi-cuadrado, que es el que nos interesa. Por tanto, no modificamos ninguna de las opciones y pulsamos Aceptar.
La ventana de salida muestra los siguientes resultados:
- En primer lugar, la tabla de doble entrada en la que se incluyen únicamente las frecuencias absolutas.
- A continuación se muestra el estadístico de contraste del test (X-squared), los grados de libertad asociados al test (df) y el p-valor (p-value).Frequency table:
Q
P Agua abajo Agua arriba
A 19 37
B 10 12
C 7 10
D 20 18
E 8 11
F 12 16
G 24 59Pearson’s Chi-squared testdata: .Table
X-squared = 7.7604, df = 6, p-value = 0.2562
Como podemos ver, el estadístico de contraste, que sigue una distribución Chi-Cuadrado con 6 grados de libertad, toma el valor 7.7604. El p-valor asociado al contraste es 0.2562. Como este p-valor es mayor que 0.05, no podemos rechazar la hipótesis nula, por lo que concluimos que la especie y la zona de avistamiento son variables independientes. Esto es, para cada especie, se observan el mismo número de peces aguas arriba y aguas abajo en el río.
Supuesto Práctico 10
Se realiza una investigación para determinar si hay alguna asociación entre el peso de un estudiante y un éxito precoz en la escuela. Se selecciona una muestra de 50 estudiantes y se clasifica a cada uno según dos criterios, el peso y el éxito en la escuela. Los datos se muestran en la tabla adjunta
\( \begin{array}{||c|c|c||} \hline Éxito/Sobrepeso & SI & NO \\ \hline SI & 162 & 263 \\ \hline NO & 38 & 37 \\ \hline \end{array} \)
Tabla 8: Datos del Supuesto Práctico 10
Contrastar, a un nivel de significación del 5%, si las dos variables estudiadas están relacionadas o si, por el contrario, son independientes.
Solución
En primer lugar vamos a introducir los datos en R-Commander. Para ello, creamos un fichero de texto como el que aparece en la Imagen

Tabla 9: Datos del Supuesto Práctico 10
A continuación, cargamos el fichero seleccionando: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra la siguiente ventana, en la cual vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Sobrepeso. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Pulsamos Aceptar y se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

Para transformar la tabla de frecuencias en un conjunto de datos (data.frame) con el que R-Commander pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script, seleccionar las tres a la vez y pulsar Ejecutar
P<-rep(Ejemplo_Sobrepeso$Exito,Ejemplo_Sobrepeso$Frecuencia)
Q<-rep(Ejemplo_Sobrepeso$Sobrepeso,Ejemplo_Sobrepeso$Frecuencia)
Exito_Sobrepeso<-data.frame(P,Q)
El nuevo conjunto de datos creado en forma de lista lo hemos llamado Éxito_Sobrepeso, y es el que tenemos que seleccionar en la pestaña de Conjunto de datos.

Pulsamos Aceptar y se muestra la siguiente pantalla

El contraste de hipótesis que se debe resolver es:
\( H_0 \equiv \) El exito en la escuela y el sobrepeso son independientes
\( H_1 \equiv \) El exito en la escuela y el sobrepeso no son independientes
Para ello, en el menú seleccionamos: Estadísticos/ Tablas de Contingencia/Tabla de doble entrada…
En la pestaña Datos tenemos que seleccionar las variables que queremos que aparezcan tanto por filas (en nuestro caso, la variable P a la que hemos asignado el Éxito) como por columnas (seleccionamos la variable Q a la que hemos asignado Sobrepeso).
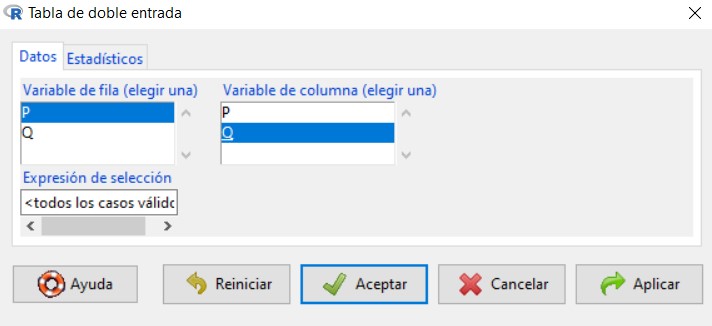
En la pestaña Estadísticos ya aparece seleccionado el Test de independencia Chi-cuadrado, que es el que nos interesa. Por tanto, no modificamos ninguna de las opciones y le damos a Aceptar.
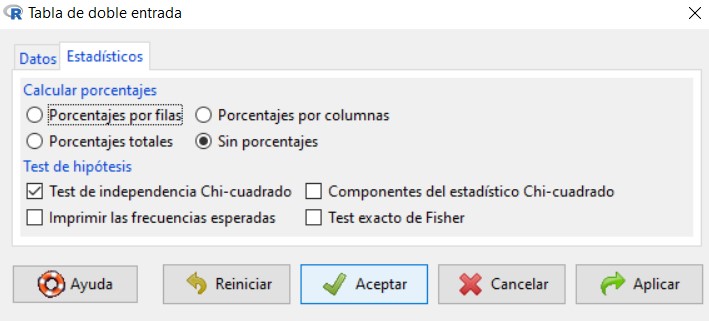
Frequency table:
Q
P No Si
No 37 38
Si 263 162
Pearson’s Chi-squared test
data: .Table
X-squared = 4.183, df = 1, p-value = 0.04083
El p-valor asociado a este contraste es 0.04083. Como este p-valor es menor que 0.05, se rechaza la hipótesis nula del contraste, por lo que concluimos que el éxito escolar y el sobrepeso son variables dependientes. Esto es, los valores de una dependen de los valores de la otra.
Otros contrastes no paramétricos
El procedimiento Prueba binomial
El procedimiento Prueba binomial compara las frecuencias observadas de las dos categorías de una variable dicotómica con las frecuencias esperadas en una distribución binomial con un parámetro de probabilidad especificado. Por defecto, el parámetro de probabilidad para ambos grupos es 0.5. Se puede cambiar el parámetro de probabilidad en el primer grupo. Siendo la probabilidad en el segundo grupo igual a uno menos la probabilidad del primer grupo.
En este procedimiento, partimos de una variable dicotómica, X. Se pretende comprobar si uno de los valores de la variable aparece en una determinada proporción, \( p_0 \). Para ello, se comparan las frecuencias observadas de dicho valor con las frecuencias esperadas de una distribución binomial donde la probabilidad de éxito viene dada por \( p_0 \). Este contraste de hipótesis, tambén llamado Contrastes de hipótesis para el parámetro p de una distribución Binomial, ya lo hemos estudiado en el apartado 6.
Recordemos que se plantean los siguientes contrastes de hipótesis:
\( \left \{ \begin{array}{c} H_0 \equiv p = p_0 \\ H_1 \equiv p \neq p_0 \end{array}\right. \)
Expresión 29: Contrates de hipótesis bilateral para el parámetro p de una Binomial
\( \left \{ \begin{array}{c} H_0 \equiv p \leq p_0 \\ H_1 \equiv p > p_0 \end{array}\right. \) \( \hspace{2cm} \left \{ \begin{array}{c} H_0 \equiv p \geq p_0 \\ H_1 \equiv p < p_0 \end{array}\right. \)
Expresión 30: Contrates de hipótesis unilateral para el parámetro p de una Binomial
Si las variables no son dicotómicas se debe especificar un punto de corte. Mediante el punto de corte se divide la variable en dos grupos, el formado por los casos mayores o iguales que el punto de corte y el formado por los casos menores que el punto de corte.
Para resolver este contraste en R-Commander se utiliza la opción Test de proporciones para una muestra, que encontramos en Estadísticos/ Proporciones/Test de proporciones para una muestra
Supuesto Práctico 11
Se quiere comprobar si la proporción de hombres y mujeres en un municipio andaluz es la misma o no. Para ello, se selecciona una muestra aleatoria de habitantes del municipio, de los cuales 258 son hombres y 216 son mujeres. A un nivel de significación del 5%, ¿puede asumirse cierta la igualdad en el número de hombres y mujeres?
Solución
Comencemos planteando las hipótesis del contraste. En este caso, se quiere probar la igualdad de hombres y de mujeres en el municipio. Para ello, es posible plantear el contraste de hipótesis de dos formas distintas. Por un lado, se puede contrastar si la proporción de hombres es de 0.5 (en cuyo caso la proporción de mujeres será también 0.5 y habrá equidad entre ambos géneros) frente a que esta proporción es distinta de 0.5. Pero, alternativamente, se puede contrastar si la proporción de mujeres es de 0.5 (lo que implica que la proporción de hombre será, igualmente, de 0.5 y habrá equidad entre géneros) frente a que esta proporción es distinta de 0.5.
En cualquier caso, el contraste a resolver es
\( \left \{ \begin{array}{c} H_0 \equiv p = 0.5 \\ H_1 \equiv p \neq 0.5 \end{array}\right. \)
Expresión 31: Contraste de hipótesis para el Supuesto práctico 11
donde p representa la proporción de hombres (o de mujeres, dependiendo de la forma de resolver el contraste que se siga) en la población.
En primer lugar, vamos a introducir los datos en R-Commander. Para ello, creamos un fichero de texto como el que aparece en la Imagen
Tabla 10: Datos del Supuesto Práctico 11
Como puede verse, en la primera fila introducimos el nombre de las variables entre comillas y separados por un espacio. A continuación, en las siguientes filas se van introduciendo los datos que aparecen en la tabla. Hay que tener en cuenta que las modalidades de las variables cualitativas hay que escribirlas entre comillas.
A continuación, cargamos el fichero seleccionando: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra la siguiente ventana en la cual vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Municipio. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Pulsamos Aceptar y se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

Para transformar la tabla de frecuencias en un conjunto de datos (data.frame) con el que R-Commander pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script, seleccionar ambas a la vez y darle a Ejecutar
P<-rep(Ejemplo_Municipio$Sexo,Ejemplo_Municipio$Frecuencia)
Sexo_Habitantes<-data.frame(P)
Para visualizar el conjunto de datos en forma de lista deberemos pulsar en el botón Conjunto de datos y seleccionar el nuevo conjunto de datos creado en forma de lista, al que hemos llamado Sexo_Habitantes.
Pulsamos Aceptar y se muestra en la pantalla principal
![]()
En esta pantalla, pulsamos en el botón Visualizar conjunto de datos podemos comprobar que la tabla de frecuencias se ha transformado en un listado de datos:

Para resolver el contraste planteado, seleccionamos en el menú: Estadísticos/ Proporciones/Test de proporciones para una muestra
Se muestra la siguiente ventana en la que tenemos dos pestañas:
- En Datos seleccionamos la variable con la que vamos a trabajar (P)
- En Opciones, tenemos que seleccionar el tipo de test que queremos realizar (bilateral o unilateral), podemos modificar el valor que vamos a darle a la proporción considerada en la hipótesis nula e incluso el nivel de confianza. Además, se proporcionan tres tipos de análisis, de los cuales vamos a seleccionar Binomial exacto que es el que nos interesa.
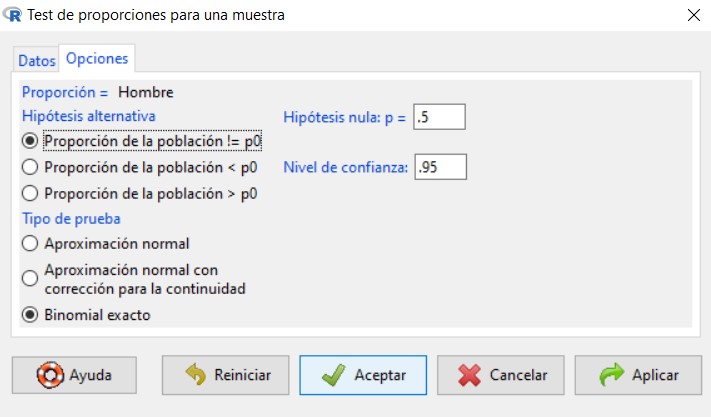
Una vez seleccionadas todas las opciones necesarias pulsamos Aceptar, y en la ventana de resultados se muestra la siguiente información:
Frequency counts (test is for first level):
P
Hombre Mujer
258 216
Exact binomial test
data: rbind(.Table)
number of successes = 258, number of trials = 474, p-value = 0.05956
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.4982562 0.5897954
sample estimates:
probability of success
0.5443038
En primer lugar, se muestra la tabla de frecuencias. A continuación, se muestran los datos de entrada que se han usado para resolver el contraste (258 hombres de 474 habitantes muestreados) así como el tipo de hipótesis alternativa (distinto de) y la proporción que se ha usado como referente para el contraste (0.5).
También aparece un p-valor, que es el que nos ayuda a resolver el contraste. En este caso, el p-valor es 0.05956. Como es mayor que 0.05, no podemos rechazar la hipótesis nula, por lo que podemos asumir que la proporción de hombres en la población es de 0.5. Consecuentemente, la proporción de mujeres también puede considerarse igual a 0.5 y puede concluirse que el número de hombres y mujeres en el municipio es el mismo.
Por último, en la salida se incluye un intervalo de confianza al nivel de confianza indicado en la llamada a binom.test (95% en nuestro caso), para la proporción de hombres en el municipio. Este intervalo es (0.4982, 0.5897). Como era de esperar, la proporción de referencia pertenece al intervalo calculado.
Como vemos, el programa considera de forma automática p como la proporción de hombres en el municipio y no nos deja modificarlo. Recordar que el resultado sería el mismo si consideráramos p como la proporción de mujeres en el municipio.
Supuesto Práctico 12
Entre los pacientes con cáncer de pulmón, el 90% o más muere generalmente en el espacio de tres años. Como resultado de nuevas formas de tratamiento, se cree que esta tasa se ha reducido. En un reciente estudio sobre 150 paciente diagnosticados de cáncer de pulmón, 128 murieron en el espacio de tres años. ¿Se puede afirmar que realmente ha disminuido la tasa de mortalidad?
Solución
En primer lugar, vamos a plantear las hipótesis del contraste.
\( \left \{ \begin{array}{l} H_0 \equiv p \geq 0.9 \hspace{.2cm} el \hspace{.2cm} tratamiento \hspace{.2cm} no \hspace{.2cm} es \hspace{.2cm} efectivo \\ H_1 \equiv p < 0.9 \hspace{.2cm} el \hspace{.2cm} tratamiento \hspace{.2cm} es \hspace{.2cm} efectivo \end{array}\right. \)
Expresión 32: Contraste de hipótesis para el Supuesto práctico 12
A continuación, utilizaremos la opción: Estadísticos/ Proporciones/Test de proporciones para una muestra
Para resolver el contraste. La información a tener en cuenta es el número de pacientes de la muestra que fallecieron (128), el número de pacientes totales en la muestra (150), la proporción que se quiere contrastar (0.9) y la forma de la hipótesis alternativa (“menor que”).
En primer lugar, vamos a introducir los datos en R-Commander. Para ello, creamos un fichero de texto como el que aparece en la Imagen

Tabla 11: Datos del Supuesto Práctico 12
Como puede verse, en la primera fila introducimos el nombre de las variables entre comillas y separados por un espacio. A continuación, en las siguientes filas se van introduciendo los datos que nos da el enunciado del problema.
Recordar, que mediante la instrucción
> library(Rcmdr)
Abrimos R_Commander. A continuación, cargamos el fichero seleccionando: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
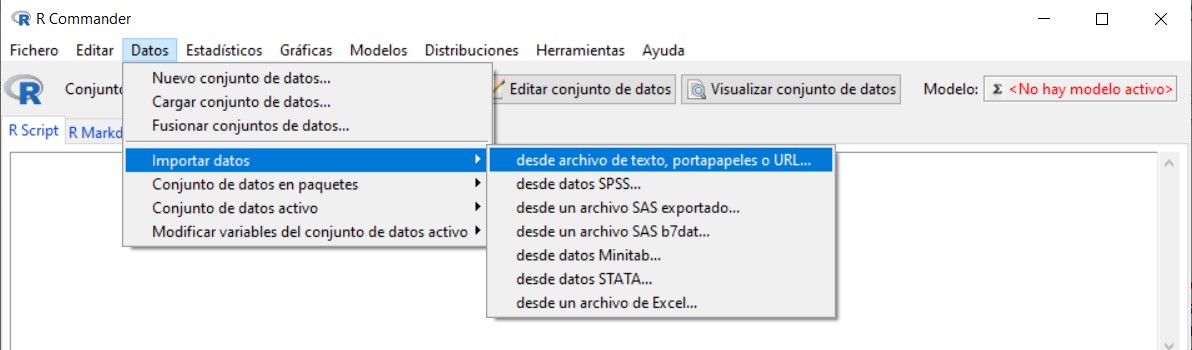
Se muestra la siguiente ventana en la cual vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Tasa_Mortalidad. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
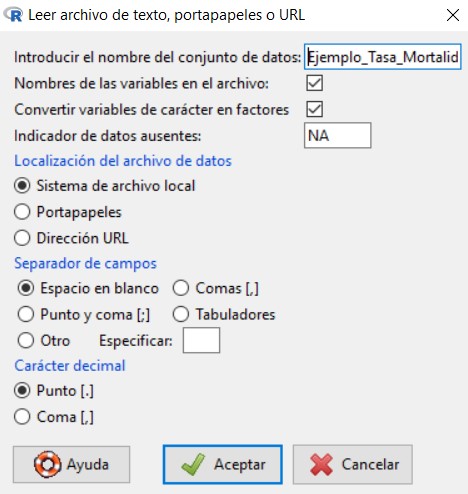
Pulsamos Aceptar y se muestra una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

Para transformar la tabla de frecuencias en un conjunto de datos (data.frame) con el que R-Commander pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script, seleccionar ambas a la vez y darle a Ejecutar:
P<-rep(Ejemplo_Tasa_Mortalidad$Tiempo,Ejemplo_Tasa_Mortalidad$Frecuencia)
Mortalidad<-data.frame(P)
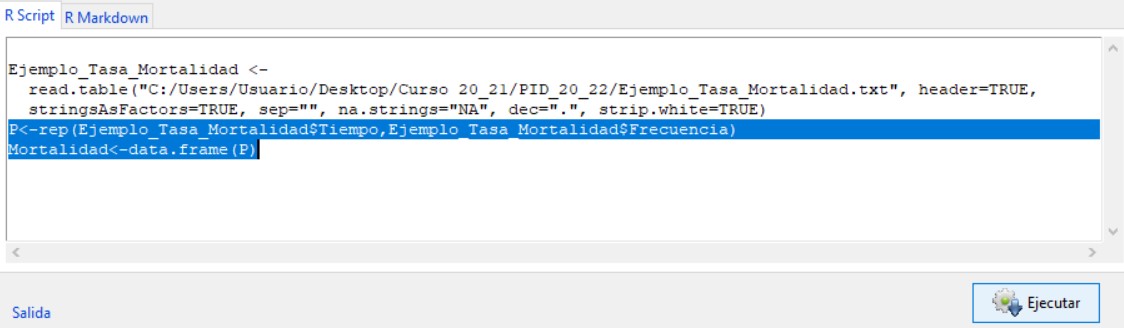
Para visualizar el conjunto de datos en forma de lista deberemos pulsar en el botón Conjunto de datos y seleccionar el nuevo conjunto de datos creado en forma de lista, al que hemos llamado Mortalidad (observar la segunda instrucción).

Para resolver el contraste planteado, seleccionamos en el menú: Estadísticos/ Proporciones/Test de proporciones para una muestra
Nos aparece la siguiente ventana en la que tenemos dos pestañas:
- En Datos seleccionamos la variable con la que vamos a trabajar (P)

- En Opciones, tenemos que seleccionar el tipo de test que queremos realizar (unilateral), podemos modificar el valor que vamos a darle a la proporción considerada en la hipótesis nula (en nuestro ejemplo 0.9) e incluso el nivel de confianza. Además, se proporcionan tres tipos de análisis, de los cuales vamos a seleccionar Binomial exacto que es el que nos interesa.
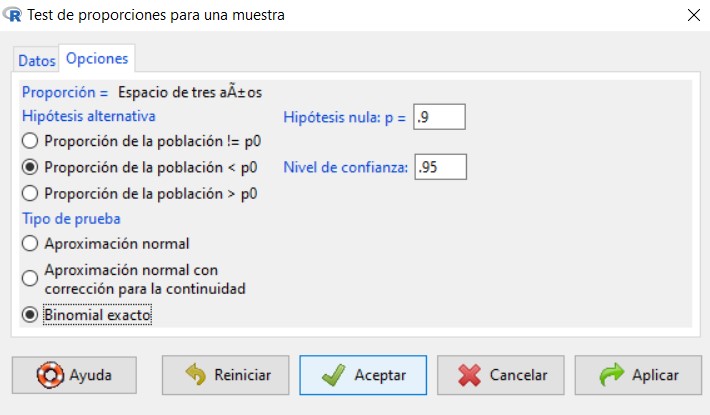
Una vez seleccionadas todas las opciones necesarias pulsamos Aceptar, y la ventana de resultados muestra la siguiente información:
Frequency counts (test is for first level):
P
Espacio de tres años Espacio superior a tres años
128 22
Exact binomial test
data: rbind(.Table)
number of successes = 128, number of trials = 150, p-value = 0.04396
alternative hypothesis: true probability of success is less than 0.9
95 percent confidence interval:
0.0000000 0.8985727
sample estimates:
probability of success
0.8533333
En la ventana de resultados se muestran la tabla de frecuencias, los datos de entrada que se han usado para resolver el contraste (128 fallecimientos en un espacio de tres años, 150 pacientes muestreados) así como el tipo de hipótesis alternativa (menor que) y la proporción que se ha usado como referente para el contraste (0.9).
También se muestra un p-valor, que es el que nos ayuda a resolver el contraste. En este caso, el p-valor es 0.04396. De manera que, considerando un nivel de significación del 5%, rechazamos la hipótesis nula, por lo que se puede concluir que la proporción de pacientes que fallecieron en el espacio de tres años es inferior a 0.9 y, consecuentemente, que el tratamiento es efectivo.
Contraste de aleatoriedad. Test de Rachas
El procedimiento Prueba de Rachas contrasta la aleatoriedad de un conjunto de observaciones de una variable continua. Para ello, el test de rachas cuenta las cadenas de valores consecutivos que presenta la variable por encima y por debajo de un determinado punto de corte. Cada uno de estas cadenas recibe el nombre de racha (de ahí el nombre del contraste). Un número muy elevado o muy reducido de rachas apuntarán hacia la no aleatoriedad de los datos que componen la muestra.
Una racha es una secuencia de observaciones similares, una sucesión de símbolos idénticos consecutivos. Ejemplo: + + – – – + – – + + + + – – – (6 rachas). Una muestra con un número excesivamente grande o excesivamente pequeño de rachas sugiere que la muestra no es aleatoria.
Las hipótesis del contraste son las siguientes:
\( H_0 \equiv \) Los datos de la muestra son aleatorios
\( H_1 \equiv \) Los datos de la muestra no son aleatorios
Para resolver este contraste con R-Commander debemos instalar y cargar el paquete randtests. Para ello, nos vamos a la ventana RGui y seleccionamos en el menú: Paquetes/Instalar paquetes(s)…
A continuación se muestra la ventana Secure CRAN mirros dónde seleccionamos Spain (Madrid).
Pulsamos OK . En la ventana Packages seleccionamos randtests y pulsamos OK.
Ya tenemos instalado el paquete. A continuación hay que cargar el paquete para poder trabajar con él. En el menú seleccionamos: Paquetes/Cargar paquete…
En la ventana Select one que se abre, seleccionamos el paquete randtests que acabamos de instalar y pulsamos Ok.
Para poder trabajar desde R-Commander con el paquete, en la ventana RScript escribimos la instrucción
library(randtests)
La seleccionamos y pulsamos Ejecutar.
A continuación, ya podemos realizar la llamada a la función runs.test. Sus argumentos son los siguientes:
runs.test (x, alternative = “two.sided”, threshold, plot)
donde
- x es un vector numérico que contiene las observaciones de la variable continua
- alternative indica el tipo de la hipótesis alternativa. Puede tomar los valores “two.sided” (hipótesis alternativa bilateral, del tipo ≠ ), que es el valor por defecto; “left.sided” (hipótesis alternativa unilateral, del tipo <) o “right.sided” (hipótesis alternativa unilateral, del tipo >).
- threshold es un valor numérico que indica el punto de corte a partir del cual se transformarán los valores del vector numérico en valores dicotómicos.
- plot es un valor lógico que indica si se incluye un gráfico en la salida o no.
Supuesto Práctico 13
Se realiza un estudio sobre el tiempo en horas de un tipo determinado de escáner antes de la primera avería. Se ha observado una muestra de 10 escáner y se ha anotado el tiempo de funcionamiento en horas: 18.21; 2.36; 17.3; 16.6; 4.70; 3.63; 15.56; 7.35; 9.78; 14.69. A un nivel de significación del 5%, ¿se puede considerar aleatoriedad en la muestra?
Solución
Formulamos el contraste que debemos resolver.
\( H_0 \equiv \) Los datos de la muestra son aleatorios
\( H_1 \equiv \) Los datos de la muestra no son aleatorios
Lo primero que vamos a hacer es crear un fichero de texto con los datos del problema con la siguiente estructura:
Tabla 12: Datos del Supuesto Práctico 13
La variable a estudiar debe aparecer en la primera fila entre comillas, y a continuación se introducen los valores numéricos que nos da el enunciado en columna y sin entrecomillar, ya que estamos trabajando con una variable cuantitativa.
A continuación, instalamos y cargamos el paquete randtests. Una vez hecho esto, cargamos el fichero de datos creado: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
En la ventana que se muestra, introducimos el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Escaner. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
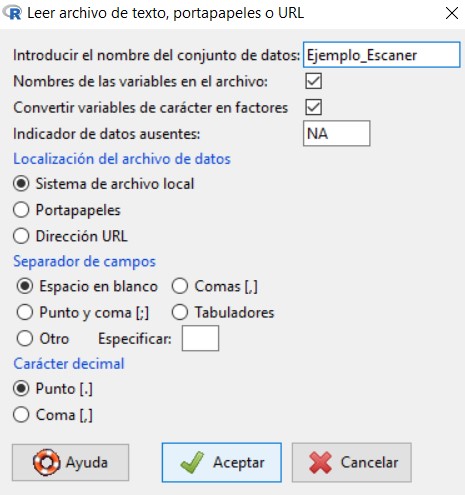
Pulsamos Aceptar y se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

A continuación, escribimos en R Script la siguiente orden para llamar a la función runs.test.
runs.test(Ejemplo_Escaner$Tiempo, alternative=”two.sided”,threshold=median(Ejemplo_Escaner$Tiempo),plot=TRUE)
Nota: Cuidado con las comillas al copiar la instrucción en R-Commander
Cuando llamamos a esta función, debemos tener en cuenta que la hipótesis alternativa es del tipo “distinto de”. Por otra parte, como el enunciado no especifica ningún punto de corte para transformar los valores del vector numérico en valores dicotómicos, este punto de corte vendrá dado por la mediana de los datos (función median en R).
Runs Test
data: Ejemplo_Escaner$Tiempo
statistic = 0.67082, runs = 7, n1 = 5, n2 = 5, n = 10, p-value = 0.5023
alternative hypothesis: nonrandomness
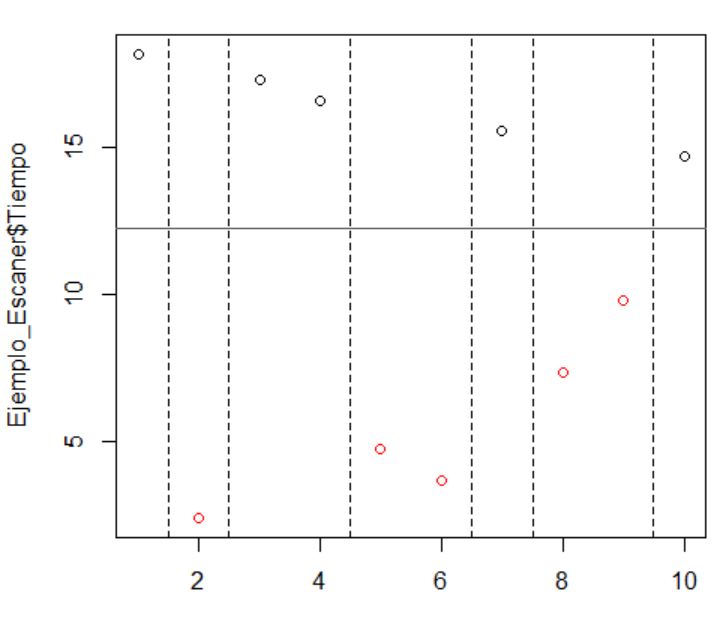
Figura 26: Representación del resultado aplicando el test de Rachas
Según los resultados del test de rachas, se han encontrado 7 rachas (runs), que vienen separadas por líneas discontinuas verticales. Hay 5 valores por encima de la mediana (\( n_1 \)), marcados en negro, y otros 5 valores por debajo de la mediana (\( n_2 \)), marcados en rojo.
El p-valor asociado al contraste es 0.5023 superior a 0.05, por lo que no es posible rechazar la hipótesis nula. Por tanto, podemos concluir que los datos de la muestra son aleatorios.
Contraste sobre bondad de ajuste: Procedimiento Prueba de Kolmogorov-Smirnov
Mediante el contraste de bondad de ajuste de Kolmogorv-Smirnov se prueba si los datos de una muestra proceden, o no, de una determinada distribución de probabilidad. Lo que se hace es comparar la función de distribución acumulada que se calcula a partir de los datos de la muestra con la función de distribución acumulada teórica de la distribución con la que se compara.
El contraste de hipótesis que se plantea es el siguiente:
\( H_0 \equiv \) Los datos de la muestra proceden de la distribución de probabilidad
\( H_1 \equiv \) Los datos de la muestra no proceden de la distribución de probabilidad
Para resolver este contraste en R-Commander se utiliza la función ks.test, que tiene los siguientes argumentos:
ks.test(x, y, …, alternative = c(“two.sided”, “less”, “greater”))
donde
- x es un vector numérico que contiene las observaciones de la variable.
- y indica la distribución de probabilidad (que ha de ser continua) que se utilizará para la comparación. Los posibles valores de este argumento son: pnorm (distribución normal), punif (distribución uniforme continua), pt (distribución t), pchisq (distribución chi-cuadrado), pf (distribución F), pexp (distribución exponencial), pgamma (distribución gamma), pweibull (distribución de Weibull) o pwilcox (distribución W de Wilcoxon).
- … Estos puntos suspensivos hacen referencia a los parámetros de la distribución, que varían de una a otra. Por ejemplo, si se elige como distribución de comparación la normal (es decir, si se asigna el valor prnom al argumento y), habrá que indicar la media y la desviación típica de dicha distribución.
- alternative indica el tipo de la hipótesis alternativa. Puede tomar los valores “two.sided” (hipótesis alternativa bilateral, del tipo ≠), que es el valor por defecto; “left.sided” (hipótesis alternativa unilateral, del tipo <) o “right.sided” (hipótesis alternativa unilateral, del tipo >).
Supuesto Práctico 14
Las puntuaciones de 10 individuos en una prueba de una oposición han sido las siguientes: 41.81, 40.30, 40.20, 37.14, 39.29, 38.79, 40.73, 39.26, 35.74, 41.65. ¿Puede suponerse, a un nivel de significación del 5% que dichas puntuaciones se ajustan a una distribución normal de media 40 y desviación típica 3?
Solución
El contraste de hipótesis que se plantea es el siguiente:
\( H_0 \equiv \) Los datos de la muestra proceden de una distribución N(40,3)
\( H_1 \equiv \) Los datos de la muestra no proceden de de una distribución N(40,3)
Lo primero que vamos a hacer es crear un fichero de texto con los datos del problema con la siguiente estructura:
Tabla 13: Datos del Supuesto Práctico 14
La variable a estudiar debe aparecer en la primera fila entre comillas, y a continuación se introducen los valores numéricos que nos da el enunciado en columna y sin entrecomillar, ya que estamos trabajando con una variable cuantitativa.
A continuación, instalamos y cargamos el paquete randtests. Una vez hecho esto, cargamos el fichero de datos creado:
Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra una ventana en la cual vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Oposicion. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
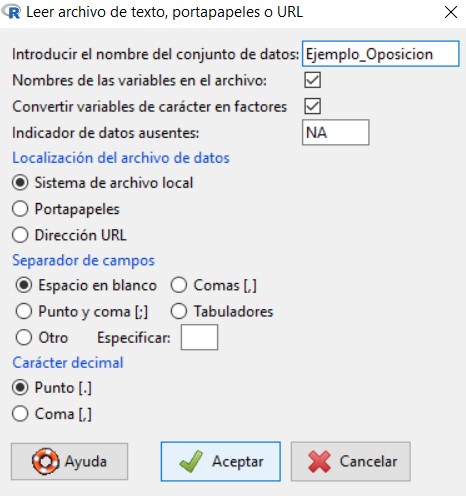
Pulsamos a Aceptar y se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.
A continuación, escribimos en R Script la siguiente orden para llamar a la función ks.test. Debemos tener en cuenta que la distribución de comparación es la distribución normal (por tanto, el argumento y tomará el valor pnorm) de media igual a 40 y desviación típica igual a 3.
A continuación, se resuelve el contraste mediante una llamada a la función ks.test. Debemos tener en cuenta que la distribución de comparación es la distribución normal (por tanto, el argumento y tomará el valor pnorm) de media igual a 40 y desviación típica igual a 3.
ks.test(Ejemplo_Oposicion$Puntuaciones,y=pnorm,40,3,alternative=”two.sided”)
En la ventana de resultados nos aparece la solución:
One-sample Kolmogorov-Smirnov test
data: Ejemplo_Oposicion$Puntuaciones
D = 0.27314, p-value = 0.3752
alternative hypothesis: two-sided
En este caso, el valor del estadístico de contraste es 0.27314 y el p-valor asociado al contraste es 0.3752. Como el p-valor es superior a 0.05 no podemos rechazar la hipótesis nula, por lo que concluimos que los datos de la muestra proceden de una distribución normal de media 40 y de desviación típica 3.
Pruebas para dos muestras independientes
El procedimiento Pruebas para dos muestras independientes compara dos grupos de casos existentes en una variable y comprueba si provienen de la misma población (homogeneidad). Estos contrastes, son la alternativa no paramétrica de los tests basados en el t de Student, Al igual que con el test de Student, se tienen dos grupos de observaciones independientes y se compara si proceden de la misma población.
El contraste que se debe resolver será alguno de los siguientes:
\( \left \{ \begin{array}{c} H_0 \equiv Me_1 – Me_2 = 0 \\ H_1 \equiv Me_1 – Me_2 \neq 0 \end{array}\right. \) \( \hspace{2cm} \left \{ \begin{array}{c} H_0 \equiv Me_1 – Me_2 = 0 \\ H_1 \equiv Me_1 – Me_2 < 0 \end{array}\right. \) \( \hspace{2cm} \left \{ \begin{array}{c} H_0 \equiv Me_1 – Me_2 = 0 \\ H_1 \equiv Me_1 – Me_2 > 0 \end{array}\right. \)
Expresión 33: Contraste de hipótesis para dos muestras independientes
O, equivalentemente,
\( \left \{ \begin{array}{c} H_0 \equiv Me_1 = Me_2 \\ H_1 \equiv Me_1 \neq Me_2 \end{array}\right. \) \( \hspace{2cm} \left \{ \begin{array}{c} H_0 \equiv Me_1 = Me_2 \\ H_1 \equiv Me_1 < Me_2 \end{array}\right. \) \( \hspace{2cm} \left \{ \begin{array}{c} H_0 \equiv Me_1 = Me_2 \\ H_1 \equiv Me_1 > Me_2 \end{array}\right. \)
Expresión 34: Contraste de hipótesis para dos muestras independientes
siendo \( Me_1 \) y \( Me_2 \) as medianas de la variable en la primera y en la segunda población, respectivamente.
La opción que resuelve estos contrastes en R-Commander es: Estadísticos/Test no paramétricos/Test de Wilcoxon para dos muestras…
Supuesto Práctico 15
En unos grandes almacenes se realiza un estudio sobre el rendimiento de ventas de los vendedores. Para ello, se observa durante 10 días el número de ventas de dos vendedores:
Vendedor A: 10 40 60 15 70 90 30 32 22 13
Vendedor B: 45 60 35 30 30 15 50 20 32 9
Contrastar, considerando un nivel de significación del 5%, si los rendimientos medianos de ambos vendedores pueden asumirse iguales.
Solución
Comenzamos creando el archivo de datos de ventas de los dos vendedores:

Tabla 14: Datos Supuesto Práctico 15
A continuación, vamos a plantear el contraste que se debe resolver
\( \left \{ \begin{array}{c} H_0 \equiv Me_A – Me_B = 0 \\ H_1 \equiv Me_A – Me_B \neq 0 \end{array}\right. \)
Expresión 35: Contraste de hipótesis para diferencia de medianas
O, equivalentemente,
\( \left \{ \begin{array}{c} H_0 \equiv Me_A = Me_B \\ H_1 \equiv Me_A \neq Me_B \end{array}\right. \)
Expresión 36: Contraste de hipótesis para diferencia de medianas
Para resolver este contraste debemos tener en cuenta que los datos proceden de muestras independientes, que el valor de la diferencia entre las medianas que se pretende comprobar es 0 y que la hipótesis alternativa del contraste es del tipo “distinto de”.
En primer lugar, cargamos el fichero seleccionando: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra una ventana en la que introducimos el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Ventas. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas y pulsamos Aceptar
Para resolver el contraste planteado, seleccionamos en el menú: Estadísticos/Test no paramétricos/Test de Wilcoxon para dos muestras…
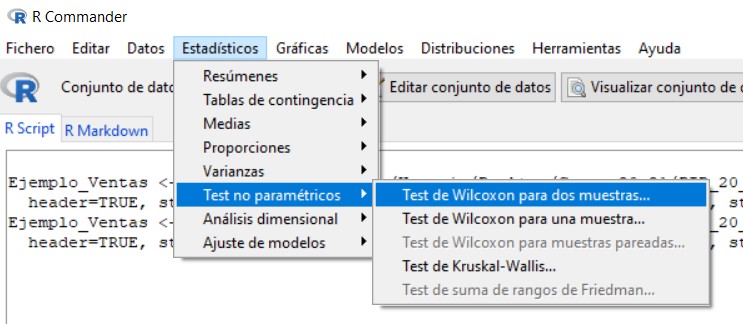
Se muestra la siguiente ventana en la que tenemos dos pestañas:
- En Datos tenemos que realizar dos selecciones: por un lado, elegir la variable “Vendedor” en la ventana de Grupos para que las comparaciones las haga entre los dos vendedores, y en la ventana Variable explicada seleccionamos la variable “Frecuencia” dónde aparecían las ventas de cada vendedor por cada uno de los 10 días.
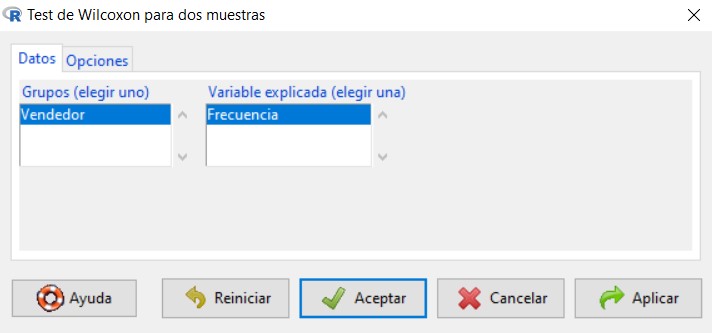
- En la pestaña Opciones, las opciones que vienen seleccionadas por defecto son las que necesitamos para resolver nuestro problema, excepto el Tipo de prueba. Si dejamos la opción “Por defecto” nos aplica el corrector por continuidad que, en nuestro caso, no vamos a aplicar. Por lo tanto, seleccionamos la opción “Exacto” y pulsamos Aceptar.
Wilcoxon rank sum test
data: Frecuencia by Vendedor
W = 52.5, p-value = 0.8497
alternative hypothesis: true location shift is not equal to 0
En este caso, el p-valor asociado al contraste es, aproximadamente, 0.8497. Como este p-valor es mayor que 0.05 no se puede rechazar la hipótesis nula, considerando un nivel de significación del 5%. Por tanto, concluimos que las medianas de las ventas de ambos vendedores pueden asumirse iguales.
Pruebas para dos muestras relacionadas
Esta prueba es similar a la anterior, con la salvedad de que ahora se supone que los datos de las muestras están relacionados, es decir, no son independientes.
Las hipótesis a contrastar son las mismas que en el caso anterior:
\( \left \{ \begin{array}{c} H_0 \equiv Me_1 – Me_2 = 0 \\ H_1 \equiv Me_1 – Me_2 \neq 0 \end{array}\right. \) \( \hspace{2cm} \left \{ \begin{array}{c} H_0 \equiv Me_1 – Me_2 = 0 \\ H_1 \equiv Me_1 – Me_2 < 0 \end{array}\right. \) \( \hspace{2cm} \left \{ \begin{array}{c} H_0 \equiv Me_1 – Me_2 = 0 \\ H_1 \equiv Me_1 – Me_2 > 0 \end{array}\right. \)
Expresión 37: Contraste de hipótesis para dos muestras relacionadas
O, equivalentemente,
\( \left \{ \begin{array}{c} H_0 \equiv Me_1 = Me_2 \\ H_1 \equiv Me_1 \neq Me_2 \end{array}\right. \) \( \hspace{2cm} \left \{ \begin{array}{c} H_0 \equiv Me_1 = Me_2 \\ H_1 \equiv Me_1 < Me_2 \end{array}\right. \) \( \hspace{2cm} \left \{ \begin{array}{c} H_0 \equiv Me_1 = Me_2 \\ H_1 \equiv Me_1 > Me_2 \end{array}\right. \)
Expresión 38: Contraste de hipótesis para dos muestras relacionadas
La opción que resuelve estos contrastes en R-Commander es: Estadísticos/Test no paramétricos/Test de Wilcoxon para muestras pareadas…
Supuesto Práctico 16
En un encinar de Navarra se pretende comprobar si un tratamiento ayuda a disminuir el nivel de húmedas de las hojas de las encinas. Para ello, se realiza un estudio a 10 encinas, en las que se seleccionan aleatoriamente 10 hojas y se registra el nivel de humedad de las hojas antes y después del tratamiento. Los resultados son los siguientes:
\( \begin{array}{||c|c|c|c|c|c|c|c|c|c|c||} \hline Antes & 10.5 & 9.7 & 13.3 & 7.5 & 12.8 & 15.2 & 11.2 & 10.7 & 5.2 & 18.9 \\ \hline Después & 11.2 & 7.8 & 9.2 & 3.4 & 8.9 & 10.8 & 11.4 & 8.5 & 6.2 & 11.1 \\ \hline \end{array} \)
Tabla 15: Datos del Supuesto Práctico 16
Suponiendo un nivel de significación del 5%, ¿Puede suponerse efectivo el tratamiento?
Solución
Comenzamos creando el archivo de datos del nivel de humedad de las hojas de las encinas:

Tabla 16: Datos del Supuesto Práctico 16
El contraste que se debe resolver es el siguiente:
\( \left \{ \begin{array}{c} H_0 \equiv Me_{Antes} = Me_{Después} \\ H_1 \equiv Me_{Antes} > Me_{Después} \end{array}\right. \)
Expresión 39: Contraste de hipótesis para Supuesto Práctico 16
En primer lugar, cargamos el fichero seleccionando: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
En la ventana resultante introducimos el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Encinas. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Pulsamos Aceptar y se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.
Para resolver el contraste planteado, seleccionamos en el menú: Estadísticos/Test no paramétricos/Test de Wilcoxon para muestras pareadas…
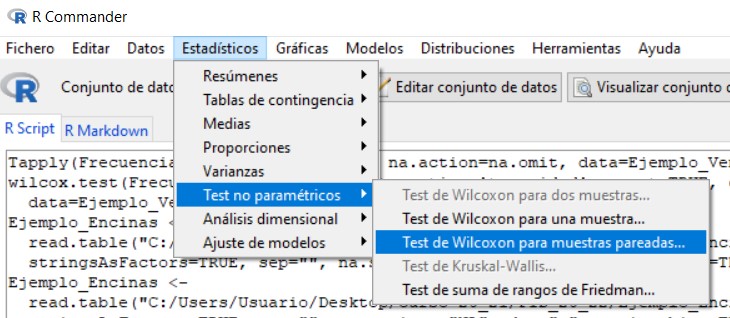
Se muestra la siguiente ventana en la que tenemos dos pestañas:
- En Datos tenemos que realizar dos selecciones: por un lado, elegir la variable que nos indica la humedad antes del tratamiento “Antes” en la ventana Primera variable, y la que nos indica la humedad después del tratamiento “Después” en la ventana Segunda variable.

- En la pestaña Opciones, necesitamos seleccionar la Hipótesis alternativa mayor que (>), enTipo de prueba seleccionamos la opción “Exacto” para que no nos aplique el corrector por continuidad y pulsamos Aceptar.
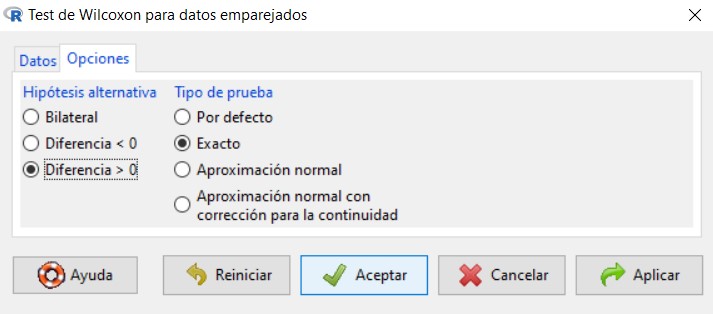
Pulsamos Aceptar y en la ventana de resultados nos aparece la siguiente información:
Wilcoxon signed rank exact test
data: Antes and Despues
V = 49, p-value = 0.01367
alternative hypothesis: true location shift is greater than 0
En este ejemplo, el p-valor asociado al contraste es 0.01367, inferior a 0.05, por lo que se rechaza la hipótesis nula considerando un nivel de significación del 5%. Esto quiere decir que el tratamiento utilizado es efectivo para reducir el nivel de humedad de las hojas de las encinas.
Ejercicios
Ejercicios Guiados
Ejercicio Guiado1
En la base de datos universidad.txt tenemos algunas variables de interés medidas para dos grupos de alumnos, dependiendo del turno de clase en el que se encuentren. El turno de mañana se define como A y el de tarde como B. Los datos se muestran en la siguiente tabla:
\( \begin{array}{||c|c|c|c||} \hline Sujeto & Grupo & CI & Estadistica \\ \hline 1 & A & 101 & Si \\ \hline 2 & B & 103 & Si \\ \hline 3 & A & 98 & No \\ \hline 4 & A & 105 & Si \\ \hline 5 & B & 99 & No \\ \hline \end{array} \)
Tabla 17: Datos del Ejercicio Guiado 1 (.txt)
Se pide:
a) Contrastar al 99% si el cociente intelectual medio es 100, sabiendo que la varianza poblacional es igual a 3
b) Contrastar al 95% de confianza si el cociente intelectual medio puede considerarse 120
c) Realizar un contraste de hipótesis a un nivel de confianza del 98% para la diferencia de medias del cociente intelectual entre el grupo A y B. ¿Puede suponerse que el cociente intelectual medio entre ambos grupos es igual?
d) Contrasta al 90% de confianza si la proporción de alumnos del grupo A es 0.5.
e) Contrasta al 90% de confianza si la proporción de alumnos del grupo B es 0.5.
f) Obtener un contraste de hipótesis a un nivel de confianza del 93% para la diferencia entre la proporción de alumnos en el grupo A y B que tienen clase de estadística.
Ejercicio Guiado 2
En un hospital se elige una muestra de pacientes y se les mide la tasa cardíaca por la mañana y a última hora de la tarde. Estudiar mediante un contraste de hipótesis al 99% si, por término medio, la tasa cardíaca es igual por la mañana y a última hora de la tarde. Los datos se muestran en la siguiente tabla
\( \begin{array}{||c|c|c||} \hline Sujeto & TCM & TCT \\ \hline 1 &58 & 65 \\ \hline 2 & 72 & 72 \\ \hline 3 & 64 & 73 \\ \hline 4 & 68 & 80 \\ \hline 5 & 67 & 63 \\ \hline \end{array} \)
Tabla 18: Datos del Ejercicio Guiado 2 (.txt)
Ejercicio Guiado 3
El ayuntamiento quiere comprobar si la ocupación del metro se produce en la misma proporción durante todos los días de la semana. Para ello, se registra el número de usuarios durante una semana cualquiera. Los datos (en miles) se recogen en la siguiente tabla:
\( \begin{array}{||c|c||} \hline Día \hspace{.2cm} de \hspace{.2cm} la & Usuarios \\ semana & \\ \hline Lunes & 32 \\ \hline Martes & 29 \\ \hline Miércoles & 35 \\ \hline Jueves & 33 \\ \hline Viernes & 29 \\ \hline Sábado & 26 \\ \hline Domingo & 10 \\ \hline \end{array} \)
Tabla 19: Datos del Ejercicio Guiado 3 (.docx)
Contrastar, a un nivel de significación del 5%, si la hipótesis de la directora del hospital puede suponerse cierta. ¿Puede asumirse que las proporciones usuarios que utilizan el metro de lunes a domingo son (0.17, 0.17, 0.17, 0.17, 0.17, 0.10, 0.05)?
Ejercicio Guiado 4
El resultado de un estudio de relación entre el dominio de la vista y el predominio de la mano viene dado en la siguiente tabla:
\( \begin{array} {|c|ccc|c|} \hline & Levocular & Ambiocular & Dextrocular & \\ \hline Zurdo & 34 & 62 & 28 &124 \\ Ambidextro & 27 & 28 & 20 & 75 \\ Dextro & 57 & 105 & 52 & 214 \\ \hline & 118 & 195 & 100 & 413 \\ \hline \end{array} \)
Tabla 20: Datos del Ejercicio Guiado 4
Contrastar, a un nivel de significación del 5%, si el dominio de la vista influye en el predominio de la mano.
Ejercicio Guiado 5
Se quiere comprobar si la proporción de hombres y mujeres en la Faculta de Educación de la Universidad de Granada es la misma o no. Para ello, se selecciona una muestra aleatoria de estudiantes de la facultad, de los cuales 1218 son hombres y 3733 son mujeres. A un nivel de significación del 5%, ¿puede asumirse cierta la igualdad en el número de hombres y mujeres estudiantes?
Ejercicio Guiado 6
Se realiza un estudio sobre el tiempo de vida en meses de la batería de un dispositivo electrónico. Se ha observado una muestra de 10 dispositivos y se ha anotado el tiempo de vida en meses: 18; 24; 17; 16; 14; 13; 15; 27; 9; 14. A un nivel de significación del 5%, ¿se puede considerar aleatoriedad en la muestra?
Ejercicio Guiado 7
Las puntuaciones de selectividad de 10 estudiantes han sido las siguientes: 10.81, 13.30, 4.20, 7.14, 9.29, 8.79, 4.73, 9.26, 5.74, 4.65. ¿Puede suponerse, a un nivel de significación del 5%, que dichas calificaciones se ajustan a una distribución normal de media 7 y desviación típica 2.5?
Ejercicio Guiado 8
En unos grandes almacenes se realiza un estudio sobre el tiempo de cobro de las cajeras por cada cliente. Para ello, se observa el número de minutos que tardan en completar el cobro de los productos de dos cajeras a diez clientes cada uno:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Cajera \hspace{.2cm} A & 10 & 4 & 6 &5 & 7& 9 & 3 & 3 & 2 & 3 \\ \hline Cajera \hspace{.2cm} B & 4 & 6 & 5 & 3 & 3 & 1 & 5 & 2 & 3 & 9 \\ \hline \end{array} \)
Tabla 21: Datos del Ejercicio Guiado 8 (.docx)
Contrastar, considerando un nivel de significación del 5%, si los tiempos medianos de ambas cajeras pueden asumirse iguales.
Ejercicio Guiado 9
En una clínica se pretende comprobar la eficacia de un tratamiento de pérdida de peso. Para ello, se realiza un estudio a 10 voluntarios, y se registra el peso antes y después del tratamiento. Los resultados son los siguientes:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Antes & 65 & 60.5 & 89.2 & 74.5 & 68.9 & 77.3 & 59.8 & 65 & 98.4 & 106 \\ \hline Despues & 64.5 & 55 & 83.6 & 73 & 64.8 & 75.1 & 56 & 60.3 & 90.7 & 94 \\ \hline \end{array} \)
Tabla 22: Datos del Ejercicio Guiado 9 (.docx)
Suponiendo un nivel de significación del 5%, ¿Puede suponerse efectivo el tratamiento?
Ejercicio Guiado 1 (Resuelto)
En la base de datos universidad.txt tenemos algunas variables de interés medidas para dos grupos de alumnos, dependiendo del turno de clase en el que se encuentren. El turno de mañana se define como A y el de tarde como B. Los datos se muestran en la siguiente tabla:
\( \begin{array}{||c|c|c|c||} \hline Sujeto & Grupo & CI & Estadistica \\ \hline 1 & A & 101 & Si \\ \hline 2 & B & 103 & Si \\ \hline 3 & A & 98 & No \\ \hline 4 & A & 105 & Si \\ \hline 5 & B & 99 & No \\ \hline \end{array} \)
Tabla 17: Datos del Ejercicio Guiado 1 (.txt)
Se pide:
a) Contrastar al 99% si el cociente intelectual medio es 100, sabiendo que la varianza poblacional es igual a 3
b) Contrastar al 95% de confianza si el cociente intelectual medio puede considerarse 120
c) Realizar un contraste de hipótesis a un nivel de confianza del 98% para la diferencia de medias del cociente intelectual entre el grupo A y B. ¿Puede suponerse que el cociente intelectual medio entre ambos grupos es igual?
d) Contrasta al 90% de confianza si la proporción de alumnos del grupo A es 0.5.
e) Contrasta al 90% de confianza si la proporción de alumnos del grupo B es 0.5.
f) Obtener un contraste de hipótesis a un nivel de confianza del 93% para la diferencia entre la proporción de alumnos en el grupo A y B que tienen clase de estadística.
Solución:
En primer lugar para trabajar con R_Commander escribimos la siguiente sentencia en R
> library(Rcmdr)
A continuación importamos los datos
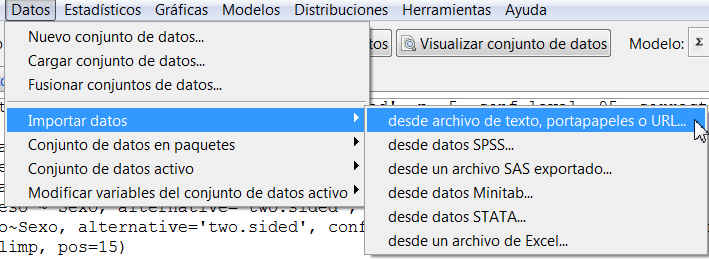
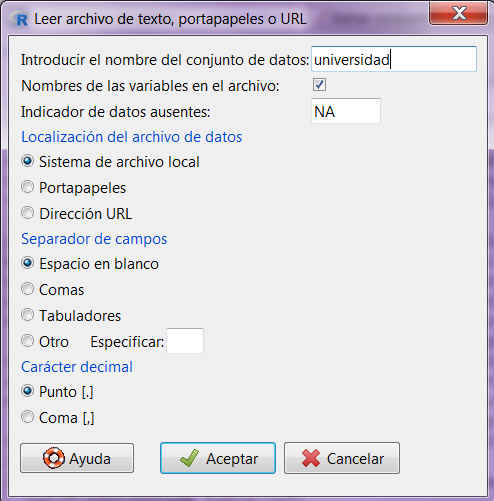
Y los visualizamos para ver que son correctos
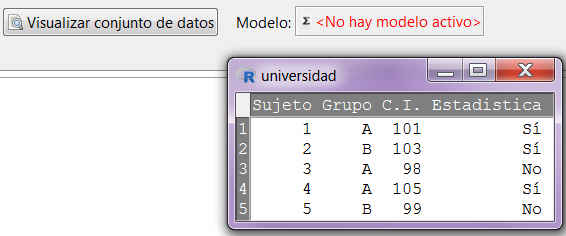
a) Contrastar al 99% si el cociente intelectual medio es 100, sabiendo que la varianza poblacional es igual a 3
En este caso nos encontramos ante un contraste de hipótesis sobre la media de una población normal con varianza conocida, por lo que hay que calcularlo mediante código
En primer lugar, planteamos el contraste de hipótesis:
\( \left \{ \begin{array}{c} H_0 \equiv \mu = 100 \\ H_1 \equiv \mu \neq 100 \end{array}\right. \)
Introducimos en R los datos relativos al nivel de significación y la varianza poblacional de la variable que proporciona el enunciado. Y calculamos el valor del estadístico y comprobamos si se cumple o no la condición de rechazo.
alpha<- 0.01
varianza <- 3
mu0 <- 100
n <- nrow(universidad)
media <- mean(universidad$C.I.)
z0 <- (media- mu0) / (sqrt(varianza) / sqrt(n))
z0
Seleccionamos todas las sentencias y pulsamos Ejecutar
[1] 1.549193
cuantil<- qnorm(1 – alpha/2)
cuantil
[1] 2.575829
Como \( |Z_{\alpha} | < Z_{1-\alpha/2} \) no tenemos evidencia muestral para rechazar la hipótesis nula, por lo que podemos considerar que el coeficiente intelectual es 100
b) Contrastar al 95% de confianza si el cociente intelectual medio puede considerarse 120
En este caso nos encontramos ante un contraste de hipótesis sobre la media de una población normal con varianza desconocida
En primer lugar, planteamos el contraste de hipótesis:
\( \left \{ \begin{array}{c} H_0 \equiv \mu = 120 \\ H_1 \equiv \mu \neq 120 \end{array}\right. \)
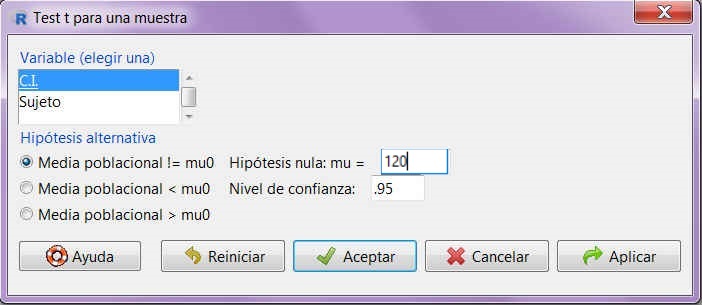
En la parte superior izquierda aparece una lista con todas las variables cuantitativas del archivo de datos que son susceptibles de ser contrastadas, de la cual debemos elegir exclusivamente una. Elegimos C.I.
En la hipótesis nula ponemos el valor a contrastar (120) y el resto de opciones las dejamos por defecto, ya que el enunciado nos pide hipótesis alternativa de distinto y nivel de confianza al 95%.
One Sample t-test
data: C.I.
t = -14.68, df = 4, p-value = 0.0001253
alternative hypothesis: true mean is not equal to 120
95 percent confidence interval:
97.64442 104.75558
sample estimates:
mean of x
101.2
La resolución del contraste se hará basándonos en el p-valor (p-value = 0.0001253)
El p-valor es una probabilidad (oscila, por lo tanto, entre 0 y 1).
-
Si el p-valor es mayor que el nivel de significación, no rechazamos la hipótesis nula.
-
Si el p-valor es menor que el nivel de significación, rechazamos la hipótesis nula en favor de la hipótesis alternativa.
En nuestro caso, el p-valor = 0.0001253 y el nivel de significación es α=0,05. Como p-valor= 0.0001253< 0,05=α, rechazamos la hipótesis nula, por lo que podemos considerar que el cociente intelectual es distinto de 120
c) Realizar un contraste de hipótesis a un nivel de confianza del 98% para la diferencia de medias del cociente intelectual entre el grupo A y B. ¿Puede suponerse que el cociente intelectual medio entre ambos grupos es igual?
En este caso nos encontramos ante contraste de hipótesis para la diferencia de medias en dos poblaciones normales independientes.
\( \left \{ \begin{array}{c} H_0 \equiv \mu_1 = \mu_2 \\ H_1 \equiv \mu_1 \neq \mu_2 \end{array}\right. \)
O equivalentemente
\( \left \{ \begin{array}{c} H_0 \equiv \mu_1 – \mu_2 = 0 \\ H_1 \equiv \mu_1 – \mu_2 \neq 0 \end{array}\right. \)
En primer lugar miramos si las varianzas de ambas distribuciones son iguales
\( \left \{ \begin{array}{c} H_0 \equiv \sigma_{1}^{2} = \sigma_{2}^{2} \\ H_1 \equiv \sigma_{1}^{2} \neq \sigma_{2}^{2} \end{array}\right. \)
O equivalentemente
\( \begin{array}{c} H_0 \equiv \displaystyle \frac{ \sigma_{1}^{2}} { \sigma_{2}^{2}} = 1 \\ H_1 \equiv \displaystyle \frac {\sigma_{1}^{2} } { \sigma_{2}^{2}} \neq 1 \end{array} \)
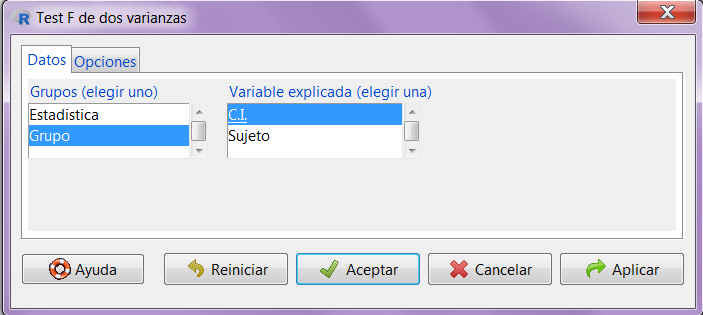
En la primera de las dos pestañas que aparecen (Datos) aparecen dos listas de variables. La lista de la izquierda (Grupos) incluye todas las variables cualitativas del fichero de datos. En esta lista tenemos que seleccionar cuál es la variable que nos va a dividir la muestra de observaciones en dos submuestras independientes. En nuestro caso, Grupo. En la lista de la derecha se incluyen las variables cuantitativas del fichero de datos. Aquí tenemos que señalar la variable principal sobre la cual se va a llevar a cabo el contraste (en nuestro caso, C.I.).

En la pestaña Opciones podemos personalizar el contraste. Dejamos la opción por defecto de bilateral y cambiamos el nivel de confianza al 98%. Pulsamos Aceptar
La salida que proporciona el programa para este test es la siguiente:
F test to compare two variances
data: C.I. by Grupo
F = 1.5417, num df = 2, denom df = 1, p-value = 0.9897
alternative hypothesis: true ratio of variances is not equal to 1
98 percent confidence interval:
0.0003083642 151.8580402010
sample estimates:
ratio of variances
1.541667
El contraste nos muestra un p valor de 0.9897 > =0.02, por lo que no tenemos evidencia muestral para rechazar, es decir, el cociente entre las dos varianzas puede tomar el valor 1 o, lo que es lo mismo, que las varianzas de los dos grupos son iguales.
Una vez se ha determinado la igualdad de las varianzas de ambas distribuciones, procedemos a calcular el contraste para la diferencia de las medias propiamente dicho.
El cuadro de diálogo que aparece muestra dos pestañas. En la primera de ellas (Datos) aparecen dos listas de variables. Como ya se ha comentado con anterioridad, en la lista de la izquierda (Grupos) tenemos que escoger la variable a partir de la cual se formarán los dos grupos de observaciones (Grupo). En la de la derecha (Variable explicada) seleccionamos la variable cuya diferencia de medias en las poblaciones queremos estudiar, (C.I.).
La segunda pestaña muestra todas las opciones del contraste que podemos modificar. Especificamos la hipótesis alternativa e indicamos si las varianzas de las dos poblaciones pueden suponerse iguales o no (dependiendo de lo obtenido en el contraste anterior). En nivel de confianza ponemos .98 y en ¿Suponer varianzas iguales seleccionamos Sí
Una vez que hemos seleccionado las variables adecuadas y hemos marcado las opciones que nos interesan, pulsamos en Aceptar, de manera que en la consola aparece una salida como esta:
Two Sample t-test
data: C.I. by Grupo
t = 0.11066, df = 3, p-value = 0.9189
alternative hypothesis: true difference in means between group A and group B is not equal to 0
98 percent confidence interval:
-13.34472 14.01139
sample estimates:
mean in group A mean in group B
101.3333 101.0000
Fijándonos en el p-valor vemos que 0.9189 > =0.02, por lo que no tenemos suficiente evidencia muestral para rechazar , es decir, podemos decir que el cociente intelectual medio del grupo A y B son iguales.
d) Contrasta al 90% de confianza si la proporción de alumnos del grupo A es 0.5.
En este caso nos encontramos ante un contraste de hipótesis para la proporción
\( \left \{ \begin{array}{c} H_0 \equiv p_A = 0.5 \\ H_1 \equiv p_A \neq 0.5 \end{array}\right. \)
Dado que la hipótesis que se ha planteado se ha hecho sobre el grupo A, no es necesario hacer ninguna recodificación de la variable.
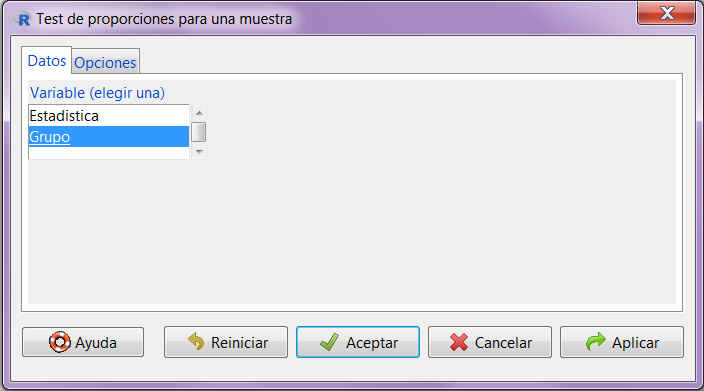
En la primera pestaña del cuadro de diálogo que aparece, encontramos una lista con todas las variables cualitativas que pueden utilizarse en este tipo de contrastes, de entre las cuales tenemos que elegir una. En este caso elegimos la variable Grupo.
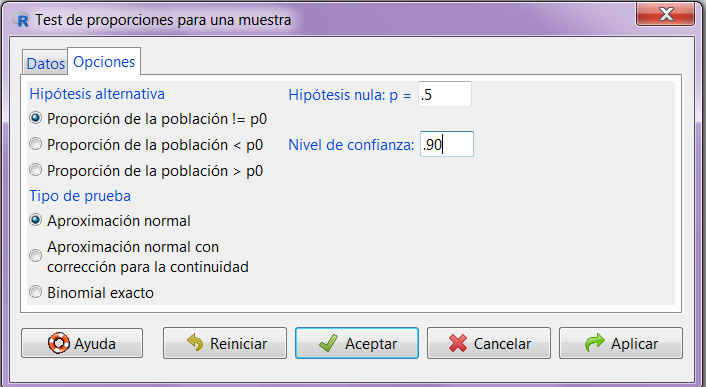
En la pestaña Opciones modificamos el valor del nivel de confianza a un 90%.
Cuando presionamos el botón Aceptar, obtenemos los resultados del análisis, que son los que se muestran a continuación:
Frequency counts (test is for first level):
Grupo
A B
3 2
1-sample proportions test without continuity correction
data: rbind(.Table), null probability 0.5
X-squared = 0.2, df = 1, p-value = 0.6547
alternative hypothesis: true p is not equal to 0.5
90 percent confidence interval:
0.2724832 0.8572935
sample estimates:
p
0.6
Por lo que si nos fijamos en el p-valor vemos que es 0.6547 > =0.1, por lo que no tenemos suficiente evidencia muestral para rechazar la hipótesis nula, es decir, la proporción de alumnos del grupo A puede considerarse igual a 0.5
e) Contrasta al 90% de confianza si la proporción de alumnos del grupo B es 0.5.
Dado que la hipótesis que se ha planteado se ha hecho sobre el grupo B es necesario hacer una recodificación de la variable.
\( \left \{ \begin{array}{c} H_0 \equiv p_B = 0.5 \\ H_1 \equiv p_B \neq 0.5 \end{array}\right. \)
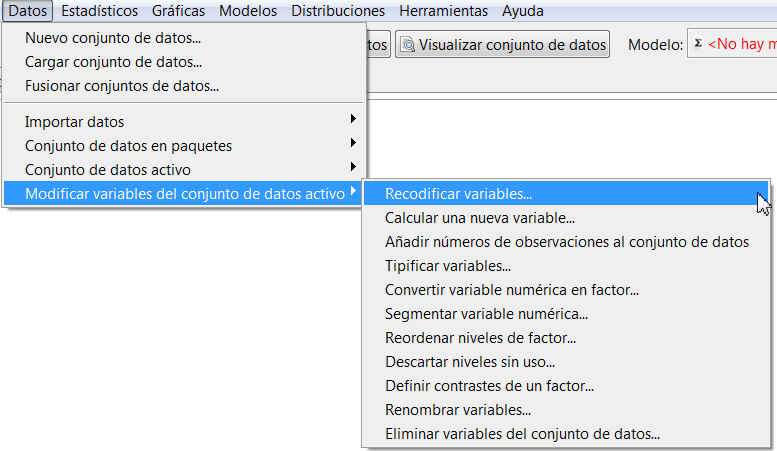
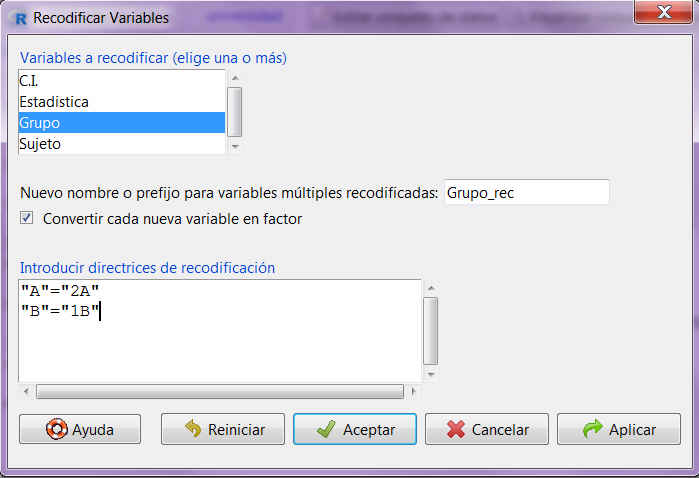
En el cuadro Variables a recodificar (elige una). Elegimos Grupo.
En el cuadro: Introducir directrices de recodificación. Una forma de recodificar la variable es ponerle un número delante del carácter. De este modo la primera categoría de la variable es aquella con el número más bajo, en este caso la B.
Pulsamos Aceptar
Tras la recodificación la base de datos quedará
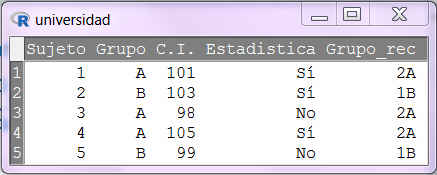
Una vez recodificada la variable, pasamos a calcular el contraste de hipótesis planteado.

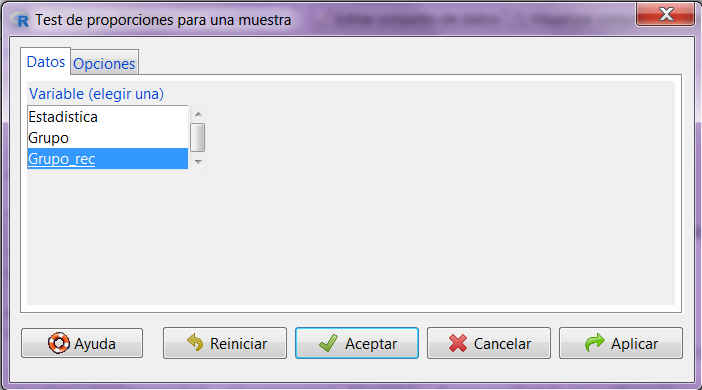
En la primera pestaña del cuadro de diálogo que aparece, encontramos una lista con todas las variables cualitativas que pueden utilizarse en este tipo de contrastes, de entre las cuales tenemos que elegir una. En este caso elegimos la variable Grupo_rec.

En la pestaña Opciones modificamos el valor del nivel de confianza a un 90%.
Cuando presionamos el botón Aceptar, obtenemos los resultados del análisis, que son los que se muestran a continuación:
Frequency counts (test is for first level):
Grupo_rec
1B 2A
2 3
1-sample proportions test without continuity correction
data: rbind(.Table), null probability 0.5
X-squared = 0.2, df = 1, p-value = 0.6547
alternative hypothesis: true p is not equal to 0.5
90 percent confidence interval:
0.1427065 0.7275168
sample estimates:
p
0.4
Observando el p-valor vemos que es 0.6547 > =0.1, por lo que no tenemos suficiente evidencia muestral para rechazar la hipótesis nula, es decir, la proporción de alumnos del grupo B puede considerarse igual a 0.5
f) Obtener un contraste de hipótesis a un nivel de confianza del 93% para la diferencia entre la proporción de alumnos en el grupo A y B que tienen clase de estadística.
En este caso nos encontramos ante un contraste de hipótesis para la diferencia de dos proporciones
\( \left \{ \begin{array}{c} H_0 \equiv p_{A_{est}} = p_{B_{est}} \\ H_1 \equiv p_{A_{est}} \neq p_{B_{est}} \end{array}\right. \)

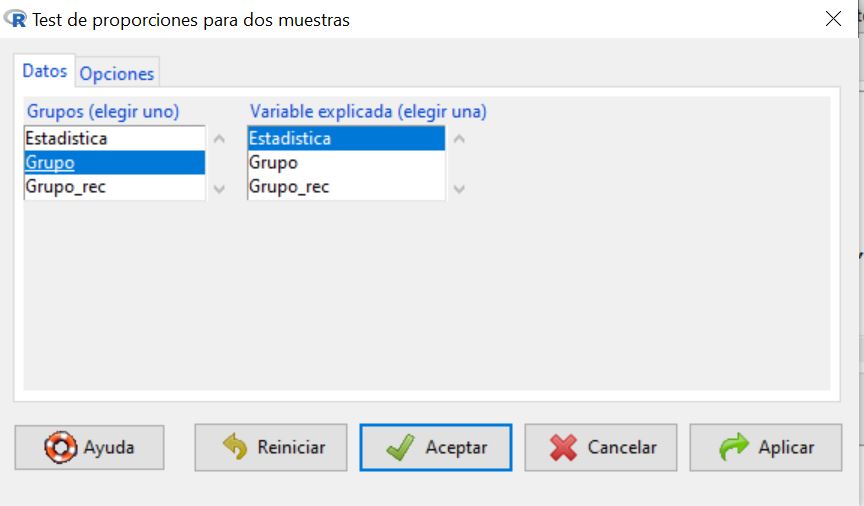
En la primera pestaña del cuadro de diálogo que muestra el programa (Datos) aparecen tres listas con las variables cualitativas que incluye el conjunto de datos. De la primera lista seleccionamos la variable de agrupación (en nuestro caso es el Grupo) y de la segunda, la variable de interés (que es, si tienen clase de estadística, Estadística).
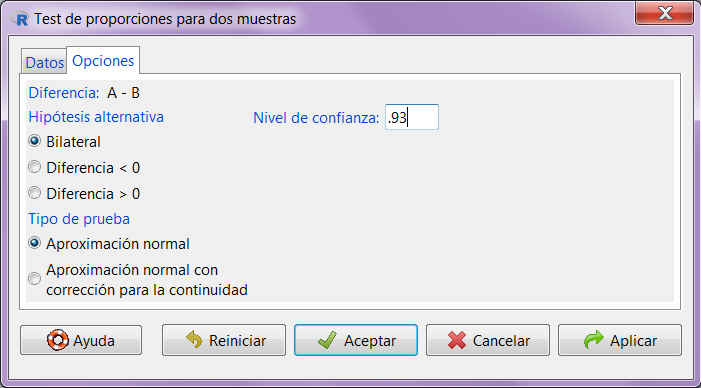
Ya en la segunda pestaña (Opciones) indicamos el nivel de confianza propuesto en el enunciado (.93).
Percentage table:
Estadistica
Grupo No Sí Total Count
A 33.3 66.7 100 3
B 50.0 50.0 100 2
2-sample test for equality of proportions without continuity correction
data: .Table
X-squared = 0.13889, df = 1, p-value = 0.7094
alternative hypothesis: two.sided
93 percent confidence interval:
-0.9750999 0.6417665
sample estimates:
prop 1 prop 2
0.3333333 0.5000000
Por último el programa devuelve la salida, y concretamente nos fijamos en el valor del p-valor=0.7094 > =0.07, por lo que no rechazamos la hipótesis nula y concluimos que las proporciones de alumnos en ambos grupos que tienen clase de estadística coinciden.
Ejercicio Guiado 2 (Resuelto)
En un hospital se elige una muestra de pacientes y se les mide la tasa cardíaca por la mañana y a última hora de la tarde. Estudiar mediante un contraste de hipótesis al 99% si, por término medio, la tasa cardíaca es igual por la mañana y a última hora de la tarde. Los datos se muestran en la siguiente tabla
\( \begin{array}{||c|c|c||} \hline Sujeto & TCM & TCT \\ \hline 1 &58 & 65 \\ \hline 2 & 72 & 72 \\ \hline 3 & 64 & 73 \\ \hline 4 & 68 & 80 \\ \hline 5 & 67 & 63 \\ \hline \end{array} \)
Tabla 18: Datos del Ejercicio Guiado 2 (.txt)
Solución:
En primer lugar para trabajar con R_Commander escribimos la siguiente sentencia en R
> library(Rcmdr)
A continuación introducimos los datos en R_Commander

Pulsamos Aceptar y se muestra la siguiente pantalla que rellenamos con los datos del ejercicio
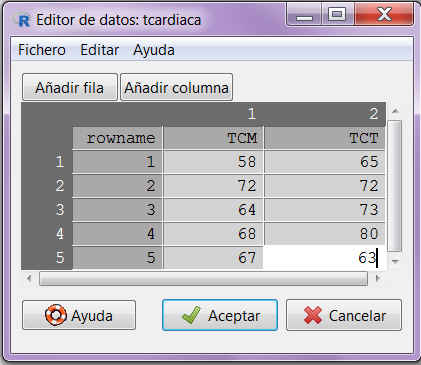
En este caso tenemos que resolver es un contraste de hipótesis para la diferencia medias en dos poblaciones normales relacionadas
\( \left \{ \begin{array}{c} H_0 \equiv \mu_{TCM} = \mu_{TCT} \\ H_1 \equiv \mu_{TCM} \neq \mu_{TCT} \end{array}\right. \)
Para ello, en el menú seleccionamos: Estadísticos/ Medias/Test para datos relacionados…..
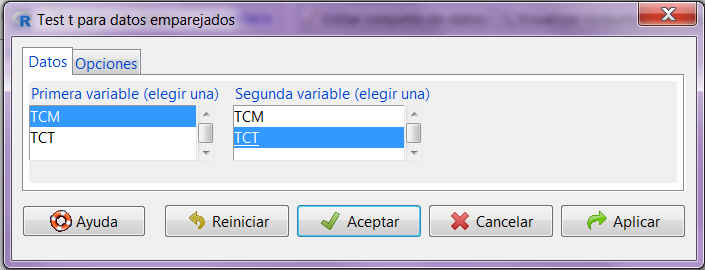
En la primera pestaña que aparece (Datos) encontramos dos listas de variables cada una de las cuales incluye todas las variables cuantitativas que son susceptibles de ser analizadas. Seleccionamos en cada lista la variable que nos convenga (TCM y TCT en nuestro caso).
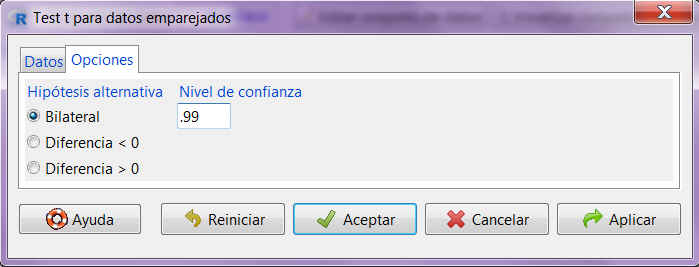
En la segunda pestaña (Opciones) podemos personalizar el contraste conforme al problema que estemos resolviendo. En este caso mantenemos la hipótesis nula en bilateral e introducimos el valor del nivel de confianza dado en el enunciado (.99). Si hacemos clic en Aceptar, el programa nos devuelve la siguiente salida:
Paired t-test
data: TCM and TCT
t = -1.6236, df = 4, p-value = 0.1798
alternative hypothesis: true difference in means is not equal to 0
99 percent confidence interval:
-18.411312 8.811312
sample estimates:
mean of the differences
-4.8
Observando el p-valor = 0.1798 > =0.01 podemos concluir que no tenemos suficiente evidencia muestral para rechazar la hipótesis nula, por lo que puede asumirse que la diferencia entre dichas medias es 0, o dicho de otro modo, que ambas tasas cardíacas son iguales.
Ejercicio Guiado 3 (Resuelto)
El ayuntamiento quiere comprobar si la ocupación del metro se produce en la misma proporción durante todos los días de la semana. Para ello, se registra el número de usuarios durante una semana cualquiera. Los datos (en miles) se recogen en la siguiente tabla:
\( \begin{array}{||c|c||} \hline Día \hspace{.2cm} de \hspace{.2cm} la & Usuarios \\ semana & \\ \hline Lunes & 32 \\ \hline Martes & 29 \\ \hline Miércoles & 35 \\ \hline Jueves & 33 \\ \hline Viernes & 29 \\ \hline Sábado & 26 \\ \hline Domingo & 10 \\ \hline \end{array} \)
Tabla 19: Datos del Ejercicio Guiado 3
Contrastar, a un nivel de significación del 5%, si la hipótesis de la directora del hospital puede suponerse cierta. ¿Puede asumirse que las proporciones usuarios que utilizan el metro de lunes a domingo son (0.17, 0.17, 0.17, 0.17, 0.17, 0.10, 0.05)?
Solución:
En primer lugar para trabajar con R_Commander escribimos la siguiente sentencia en R
> library(Rcmdr)
A continuación introducimos los datos en R-Commander. Para ello, tenemos que crear un fichero de texto como el que aparece en la Imagen.

Tabla 23: Datos del Ejercicio Guiado 3
Como puede verse, en la primera fila introducimos el nombre de las variables entre comillas y separados por un espacio. A continuación, en las siguientes filas se van introduciendo los datos que aparecen en la tabla. Hay que tener en cuenta que las modalidades de las variables cualitativas hay que escribirlas entre comillas.
A continuación, cargamos el fichero seleccionando: Datos/Importar datos/desde archivo de texto, portapapeles o URL…

Se muestra la siguiente ventana en la cual vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Metro. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
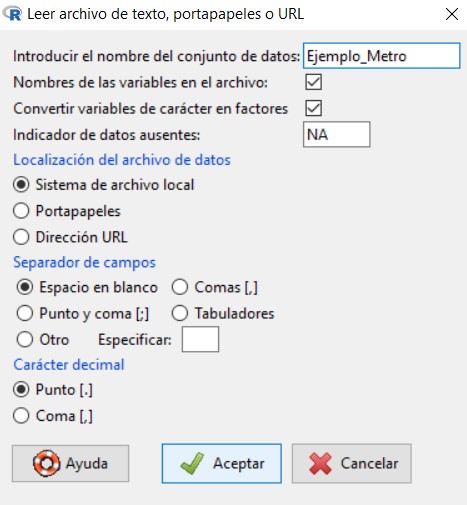
Pulsamos Aceptar y se muestra una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

Para transformar la tabla de frecuencias en un conjunto de datos (data.frame) con el que R-Commander pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script, seleccionar ambas a la vez y darle a Ejecutar:
P<-rep(Ejemplo_Metro$Dias,Ejemplo_Metro$Frecuencia)
Afluencia_diaria<-data.frame(P)
Con esto conseguimos que la variable P contenga los datos en forma de lista y que el nuevo archivo de datos con el que vamos a trabajar se llame Afluencia_diaria.
Para visualizar el nuevo conjunto de datos, pulsamos en el botón Conjunto de datos y seleccionamos Afluencia_diaria. Una vez seleccionado, si pulsamos en el botón Visualizar conjunto de datos podemos comprobar el nuevo formato de los datos.
El contraste de hipótesis que debemos resolver es
\( H_0 \equiv \) La ocupación del metro se produce en la misma proporción todos los días de la semana
\( H_1 \equiv \) La ocupación del metro no se producen en la misma proporción todos los días de la semana
Expresión 40: Contraste de hipótesis para el Ejercicio Guiado1
Para ello, en el menú seleccionamos: Estadísticos/ Resúmenes/Distribución de frecuencias

Se muestra la siguiente ventana en la que tenemos que seleccionar la variable en estudio (P), clickar en Test Chi-Cuadrado y pulsar Aceptar.
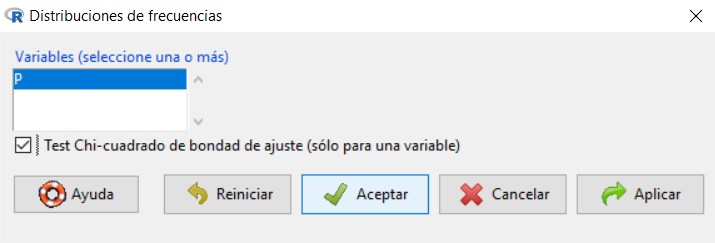
El siguiente paso es introducir las proporciones que queremos contrastar.
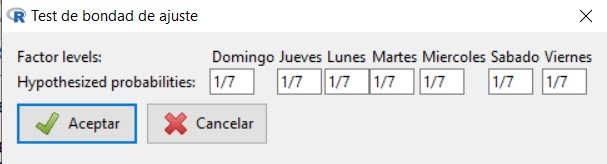
Por defecto, aparece la misma proporción para todos los días de la semana y, como en este caso, es lo que queremos comprobar (ver \( H_0 \equiv \) ), pulsamos Aceptar sin modificar nada.
Notar que R-Commander ordena las modalidades de las variables cualitativas por orden alfabético. Por este motivo, hay que tener cuidado cuando se introducen los datos.
En la ventana de resultados nos aparece la siguiente información:
- En primer lugar, las frecuencias absolutas de la ocupación (en miles) para cada día de la semana.
- A continuación, se no proporcionan los porcentajes de ocupación por día.
- Para finalizar aparece el estadístico de contraste del Test Chi-Cuadrado (X-squared), los grados de libertad de la distribución Chi-Cuadrado para este ejemplo (df) y, por último, el p-valor asociado al contraste (p-value).
counts:
P
Domingo Jueves Lunes Martes Miercoles Sabado Viernes
10 33 32 29 35 26 29
percentages:
P
Domingo Jueves Lunes Martes Miercoles Sabado Viernes
5.15 17.01 16.49 14.95 18.04 13.40 14.95
Chi-squared test for given probabilities
data: .Table
X-squared = 15.134, df = 6, p-value = 0.01924
El estadístico de contraste, que sigue una distribución Chi-cuadrado, toma el valor 15.134. Los grados de libertad de la distribución Chi-cuadrado para este ejemplo son 6. El p-valor asociado al contraste es menor que 0.05 por lo que, considerando un nivel de significación del 5%, se rechaza la hipótesis nula. Es decir, se concluye que la ocupación del metro no se produce en la misma proporción todos los días de la semana.
Para comprobar si podemos asumir que las proporciones de ocupación correspondientes a cada día de la semana (de Lunes a Domingo) son (0.17, 0.17, 0.17, 0.17, 0.17, 0.10, 0.05), seguimos los mismos pasos, pero teniendo en cuenta que, ahora, tenemos que introducir los valores de las nuevas proporciones consideradas.
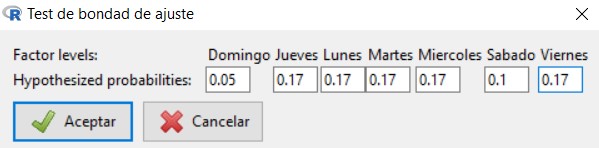
counts:
P
Domingo Jueves Lunes Martes Miercoles Sabado Viernes
10 33 32 29 35 26 29
percentages:
P
Domingo Jueves Lunes Martes Miercoles Sabado Viernes
5.15 17.01 16.49 14.95 18.04 13.40 14.95
Chi-squared test for given probabilities
data: .Table
X-squared = 3.3681, df = 6, p-value = 0.7614
En este caso, el valor del estadístico de contraste es 3.3681. El p-valor asociado es 0.7614 que, al ser superior a 0.05, nos indica que no se puede rechazar la hipótesis nula. Esto equivale a decir que, a un nivel de significación del 5%, puede suponerse que la ocupación del metro se produce según los valores de las proporciones consideradas.
Ejercicio Guiado 4 (Resuelto)
El resultado de un estudio de relación entre el dominio de la vista y el predominio de la mano viene dado en la siguiente tabla:
\( \begin{array} {|c|ccc|c|} \hline & Levocular & Ambiocular & Dextrocular & \\ \hline Zurdo & 34 & 62 & 28 &124 \\ Ambidextro & 27 & 28 & 20 & 75 \\ Dextro & 57 & 105 & 52 & 214 \\ \hline & 118 & 195 & 100 & 413 \\ \hline \end{array} \)
Tabla 20: Datos del Ejercicio Guiado 4(.docx)
Contrastar, a un nivel de significación del 5%, si el dominio de la vista influye en el predominio de la mano.
Solución:
En primer lugar para trabajar con R_Commander escribimos la siguiente sentencia en R
> library(Rcmdr)
A continuación introducimos los datos en R-Commander. Para ello, tenemos que crear un fichero de texto como el que aparece en la Imagen.

Tabla 24: Datos del Ejercicio Guiado 4 (.txt)
Como se puede observar, en la primera fila introducimos el nombre de las variables entre comillas y separados por un espacio. A continuación, en las siguientes filas se van introduciendo los datos que aparecen en la tabla. Hay que tener en cuenta que las modalidades de las variables cualitativas hay que escribirlas entre comillas.
A continuación, cargamos el fichero creado mediante las siguientes instrucciones: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra una ventana en la cual vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_VistaMano. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
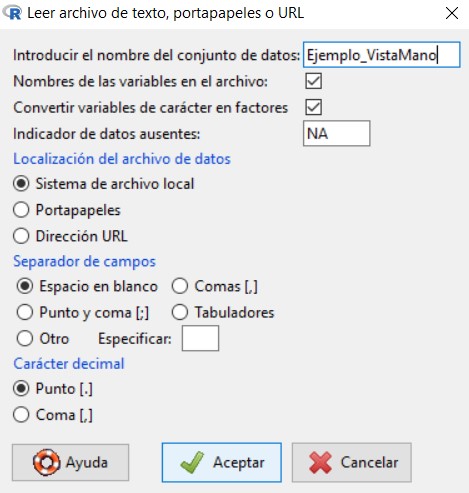
Pulsamos Aceptar y se muestra una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

Para transformar la tabla de contingencia en un conjunto de datos (data.frame) con el que R-Commander pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script, seleccionar las tres a la vez y darle a Ejecutar:
P<-rep(Ejemplo_VistaMano$Vista,Ejemplo_VistaMano$Frecuencia)
Q<-rep(Ejemplo_VistaMano$Mano,Ejemplo_VistaMano$Frecuencia)
Vista_Mano<-data.frame(P,Q)
Para visualizar el conjunto de datos en forma de lista deberemos pulsar en el botón Conjunto de datos y seleccionar el nuevo conjunto de datos creado, al que hemos llamado Vista_Mano (observar la tercera instrucción).

Una vez seleccionado, si pulsamos en el botón Visualizar conjunto de datos podemos comprobar que la tabla de frecuencias se ha transformado en un listado de datos.
El contraste de hipótesis que se debe resolver es:
\( H_0 \equiv \) El dominio de la vista y el predominio de la mano son independientes
\( H_1 \equiv \) El dominio de la vista y el predominio de la mano no son independientes
Expresión 41: Contraste de hipótesis para el Ejercicio Guiado2
Para ello, en el menú seleccionamos las opciones: Estadísticos/Tablas de contingencia/Tabla de doble entrada
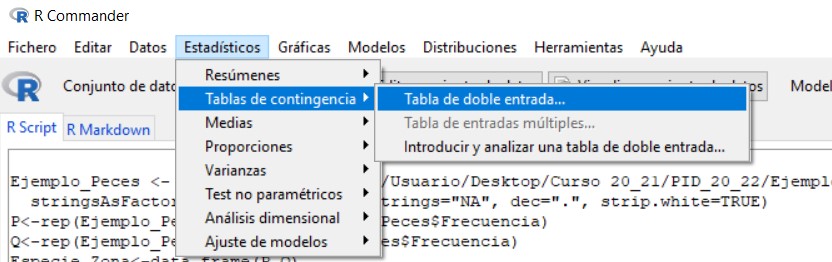
Se muestra la siguiente ventana que presenta dos pestañas. En la pestaña Datos tenemos que seleccionar las variables que queremos que aparezcan tanto por filas (en nuestro caso, la variable P a la que hemos asignado el dominio de la vista) como por columnas (seleccionamos la variable Q a la que hemos asignado el predominio de la mano).
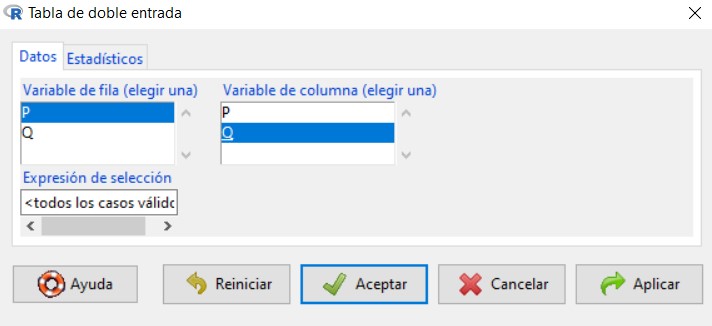
En la pestaña Estadísticos tenemos la opción de incluir algún porcentaje en la tabla de doble entrada, aunque por defecto aparece sin porcentajes. En principio, lo vamos a dejar así. También aparece seleccionado el Test de independencia Chi-cuadrado, que es el que nos interesa. Por tanto, no modificamos ninguna de las opciones y le damos a Aceptar.
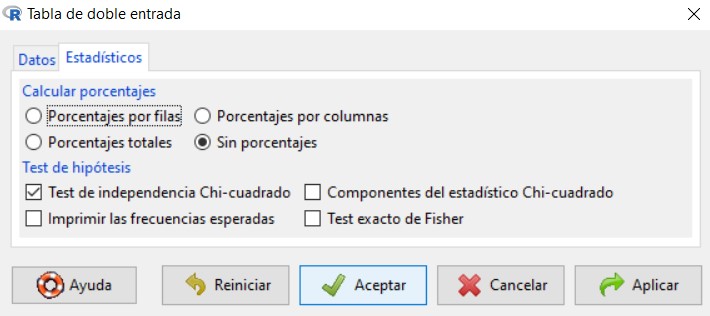
En la ventana de salida se muestran los siguientes resultados:
- La tabla de doble entrada en la que se incluyen únicamente las frecuencias absolutas.
- El estadístico de contraste del test (X-squared), los grados de libertad asociados al test (df) y el p-valor (p-value).
Frequency table:
Q
P Ambiocular Dextrocular Levolular
Ambidextro 28 20 27
Dextro 105 52 57
Zurdo 62 28 34
Pearson’s Chi-squared test
data: .Table
X-squared = 4.0205, df = 4, p-value = 0.4032
Como podemos ver, el estadístico de contraste, que sigue una distribución Chi-Cuadrado con 4 grados de libertad, toma el valor 4.0205. El p-valor asociado al contraste es 0.4032. Como este p-valor es mayor que 0.05, no podemos rechazar la hipótesis nula, por lo que concluimos que el dominio de la vista y el predominio de la mano son variables independientes.
Ejercicio Guiado 5 (Resuelto)
Se quiere comprobar si la proporción de hombres y mujeres en la Faculta de Educación de la Universidad de Granada es la misma o no. Para ello, se selecciona una muestra aleatoria de estudiantes de la facultad, de los cuales 1218 son hombres y 3733 son mujeres. A un nivel de significación del 5%, ¿puede asumirse cierta la igualdad en el número de hombres y mujeres estudiantes?
Solución:
Comencemos planteando las hipótesis del contraste. En este caso, se quiere probar la igualdad de hombres y de mujeres en la Faculta de Educación de la Universidad de Granada. Para ello, es posible plantear el contraste de hipótesis de dos formas distintas. Por un lado, se puede contrastar si la proporción de hombres es de 0.5 (en cuyo caso la proporción de mujeres será también 0.5 y habrá equidad entre ambos géneros) frente a que esta proporción es distinta de 0.5. Pero, alternativamente, se puede contrastar si la proporción de mujeres es de 0.5 (lo que implica que la proporción de hombre será, igualmente, de 0.5 y habrá equidad entre géneros) frente a que esta proporción es distinta de 0.5.
En cualquier caso, ambas situaciones son equivalente y el contraste a resolver es
\( \left \{ \begin{array}{c} H_0 \equiv p=0.5 \\ H_1 \equiv p \neq 0.5 \end{array}\right. \)
Expresión 42: Contraste de hipótesis para el Ejercicio Guiado 5
donde p representa la proporción de hombres (o de mujeres, dependiendo de la forma de resolver el contraste que se siga) en la población.
En primer lugar para trabajar con R_Commander escribimos la siguiente sentencia en R
> library(Rcmdr)
A continuación introducimos los datos en R-Commander. Para ello, creamos un fichero de texto como el que aparece en la Imagen.
 Tabla 25: Datos del Ejercicio Guiado 5
Tabla 25: Datos del Ejercicio Guiado 5
Como puede verse, en la primera fila introducimos el nombre de las variables entre comillas y separados por un espacio. A continuación, en las siguientes filas se van introduciendo los datos que aparecen en la tabla. Hay que tener en cuenta que las modalidades de las variables cualitativas hay que escribirlas entre comillas.
A continuación, cargamos el fichero seleccionando: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra la siguiente ventana en la cual vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Facultad. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
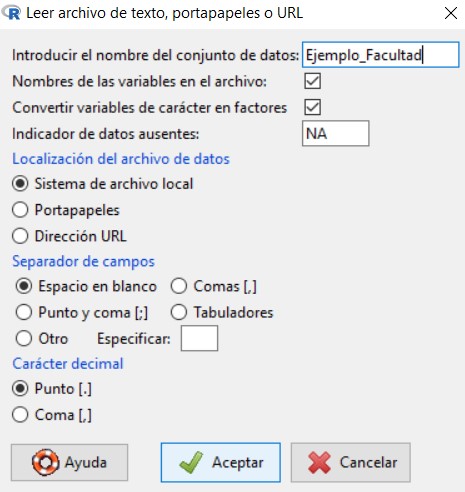
Pulsamos Aceptar se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

Para transformar la tabla de frecuencias en un conjunto de datos (data.frame) con el que R pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script, seleccionar ambas a la vez y darle a Ejecutar
P<-rep(Ejemplo_Facultad$Sexo,Ejemplo_Facultad$Frecuencia)
Sexo_Facultad<-data.frame(P)
Para visualizar el conjunto de datos en forma de lista deberemos pulsar en el botón Conjunto de datos y seleccionar el nuevo conjunto de datos creado en forma de lista, al que hemos llamado Sexo_Facultad (observar la segunda instrucción). Una vez seleccionado, si pulsamos en el botón Visualizar conjunto de datos podemos comprobar que la tabla de frecuencias se ha transformado en un listado de datos.

Para resolver el contraste planteado, seleccionamos en el menú: Estadísticos/ Proporciones/Test de proporciones para una muestra
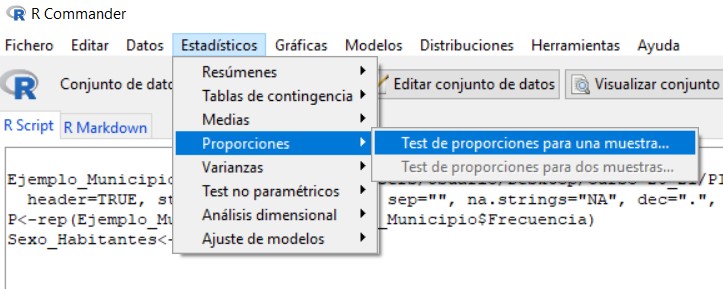
Nos aparece la siguiente ventana en la que tenemos dos pestañas:
- En Datos seleccionamos la variable con la que vamos a trabajar (P)
- En Opciones, tenemos que seleccionar el tipo de test que queremos realizar (bilateral o unilateral), podemos modificar el valor que vamos a darle a la proporción considerada en la hipótesis nula e incluso el nivel de confianza. Además, se proporcionan tres tipos de análisis, de los cuales vamos a seleccionar Binomial exacto que es el que nos interesa.
Notar que R-Commander ha tenido en cuenta la categoría de “Hombre” en la hipótesis nula.
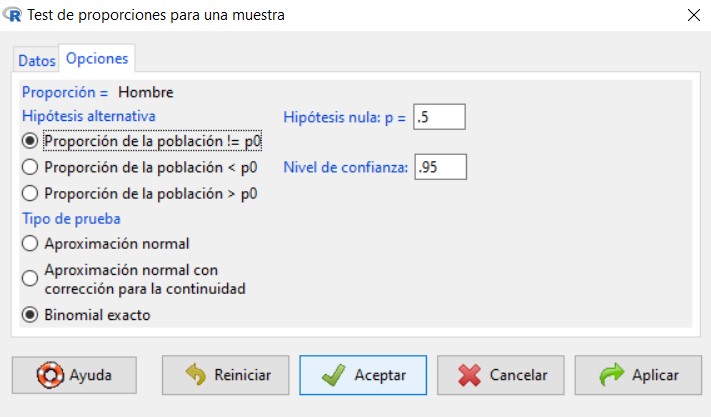
Una vez seleccionadas todas las opciones necesarias pulsamos Aceptar, y en la ventana de resultados nos aparece la siguiente información:
Frequency counts (test is for first level):
P
Hombre Mujer
1218 3733
Exact binomial test
data: rbind(.Table)
number of successes = 1218, number of trials = 4951, p-value < 2.2e-16
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.2340658 0.2582562
sample estimates:
probability of success
0.2460109
En primer lugar, se muestra la tabla de frecuencias. A continuación, los datos de entrada que se han usado para resolver el contraste (1218 hombres de 4951 estudiantes muestreados) así como el tipo de hipótesis alternativa (distinto de) y la proporción que se ha usado como referente para el contraste (0.5).
También se muestra un p-valor, que es el que nos ayuda a resolver el contraste. En este caso, el p-valor es menor que 0.05, por lo que podemos rechazar la hipótesis nula, asumiendo que la proporción de hombres en la Facultad de Educación de la Universidad de Granada no es de 0.5. Consecuentemente, la proporción de mujeres tampoco puede considerarse igual a 0.5 y puede concluirse que el número de hombres y mujeres en la facultad no es el mismo.
Por último, en la salida se incluye un intervalo de confianza al nivel de confianza indicado (95% por defecto), para la proporción de hombres en el municipio. Este intervalo es (0.234, 0.258). Como era de esperar, la proporción hombres que cursan estudios en la Facultad de Educación es inferior al de mujeres.
> t.test(Rio1, Rio2, alternative = “two.sided”, mu = 0, var.equal = TRUE, conf.level = 0.90)
Two Sample t-test
data: Rio1 and Rio2
t = 2.2564, df = 17, p-value = 0.0375
alternative hypothesis: true difference in means is not equal to 0
90 percent confidence interval:
0.424258 3.280287
sample estimates:
mean of x mean of y
10.72727 8.87500
En este caso, el p-valor asociado al contraste es 0.0375, que es menor que 0.10, el nivel de significación. Por tanto, rechazamos la hipótesis nula y concluimos que la cantidad media de tóxico en ambos ríos no es la misma.
Ejercicio Guiado 6 (Resuelto)
Se realiza un estudio sobre el tiempo de vida en meses de la batería de un dispositivo electrónico. Se ha observado una muestra de 10 dispositivos y se ha anotado el tiempo de vida en meses: 18; 24; 17; 16; 14; 13; 15; 27; 9; 14. A un nivel de significación del 5%, ¿se puede considerar aleatoriedad en la muestra?
Solución:
Formulamos el contraste que debemos resolver.
\( H_0 \equiv \) Los datos de la muestra son aleatorios
\( H_1 \equiv \) Los datos de la muestra no son aleatorios
Lo primero que vamos a hacer es crear un fichero de texto con los datos del problema con la siguiente estructura:
 Tabla 26: Datos del Ejercicio Guiado 6
Tabla 26: Datos del Ejercicio Guiado 6
La variable a estudiar debe aparecer en la primera fila entre comillas, y a continuación se introducen los valores numéricos que nos da el enunciado en columna y sin entrecomillar, ya que estamos trabajando con una variable cuantitativa.
En primer lugar para trabajar con R_Commander escribimos la siguiente sentencia en R
> library(Rcmdr)
A continuación, instalamos y cargamos el paquete randtests. Una vez hecho esto, cargamos el fichero de datos creado: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra la siguiente ventana en la cual vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Dispositivos. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
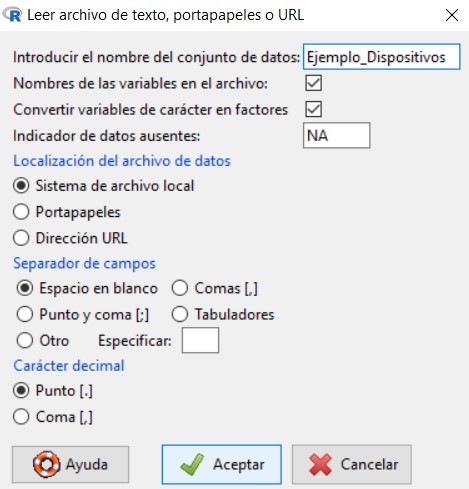
Pulsamos Aceptar y se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

A continuación, escribimos en R Script la siguiente orden para llamar a la función runs.test
randtests::runs.test (Ejemplo_Dispositivos$Tiempo, alternative=”two.sided”,threshold=median(Ejemplo_Dispositivos$Tiempo),plot=TRUE)
Nota: Cuidado con las comillas “”
Cuando llamamos a esta función, debemos tener en cuenta que la hipótesis alternativa es del tipo “distinto de”. Por otra parte, como el enunciado no especifica ningún punto de corte para transformar los valores del vector numérico en valores dicotómicos, este punto de corte vendrá dado por la mediana de los datos (función median en R).
Runs Test
data: Ejemplo_Dispositivos$Tiempo
statistic = -1.3416, runs = 4, n1 = 5, n2 = 5, n = 10, p-value = 0.1797
alternative hypothesis: nonrandomness
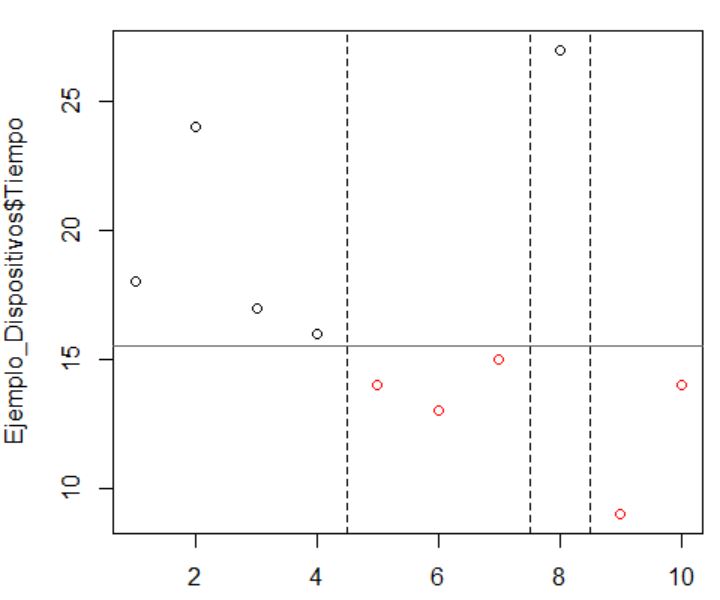
Figura 27: Representación del resultado aplicando el test de Rachas
Según los resultados del test de rachas, se han encontrado 4 rachas (runs), que vienen separadas por líneas discontinuas verticales. Hay 5 valores por encima de la mediana (n1), marcados en negro, y otros 5 valores por debajo de la mediana (n2), marcados en rojo.
El p-valor asociado al contraste es 0.1797 superior a 0.05, por lo que no es posible rechazar la hipótesis nula. Por tanto, podemos concluir que los datos de la muestra son aleatorios
Ejercicio Guiado 7 (Resuelto)
Las puntuaciones de selectividad de 10 estudiantes han sido las siguientes: 10.81, 13.30, 4.20, 7.14, 9.29, 8.79, 4.73, 9.26, 5.74, 4.65. ¿Puede suponerse, a un nivel de significación del 5%, que dichas calificaciones se ajustan a una distribución normal de media 7 y desviación típica 2.5?
Solución:
El contraste de hipótesis que se plantea es el siguiente:
\( H_0 \equiv \) Los datos de la muestra proceden de una distribución N(7,2.5)
\( H_1 \equiv \) Los datos de la muestra no proceden de una distribución N(7,2.5)
Expresión 45: Contraste de hipótesis para el Ejercicio Guiado 7
Lo primero que vamos a hacer es crear un fichero de texto con los datos del problema con la siguiente estructura:

Tabla 27: Datos del Ejercicio Guiado 7
La variable a estudiar debe aparecer en la primera fila entre comillas, y a continuación se introducen los valores numéricos que nos da el enunciado en columna y sin entrecomillar, ya que estamos trabajando con una variable cuantitativa.
A continuación, instalamos y cargamos el paquete randtests. Una vez hecho esto, cargamos el fichero de datos creado: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra la siguiente ventana en la que vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Selectividad. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Pulsamos Aceptar y se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

A continuación, escribimos en R Script la siguiente orden para llamar a la función ks.test. Debemos tener en cuenta que la distribución de comparación es la distribución normal (por tanto, el argumento y tomará el valor pnorm) de media igual a 7 y desviación típica igual a 2.5.
ks.test(Ejemplo_Selectividad$Calificaciones,y=pnorm,7,2.5,alternative=”two.sided”)
La ventana de resultados muestra la siguiente solución
One-sample Kolmogorov-Smirnov test
data: Ejemplo_Selectividad$Calificaciones
D = 0.263, p-value = 0.421
alternative hypothesis: two-sided
En este caso, el valor del estadístico de contraste es 0.263 y el p-valor asociado al contraste es 0.421. Como el p-valor es superior a 0.05 no podemos rechazar la hipótesis nula, por lo que concluimos que los datos de la muestra proceden de una distribución normal de media 7 y de desviación típica 2.5.
Ejercicio Guiado 8 (Resuelto)
En unos grandes almacenes se realiza un estudio sobre el tiempo de cobro de las cajeras por cada cliente. Para ello, se observa el número de minutos que tardan en completar el cobro de los productos de dos cajeras a diez clientes cada uno:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Cajera \hspace{.2cm} A & 10 & 4 & 6 &5 & 7& 9 & 3 & 3 & 2 & 3 \\ \hline Cajera \hspace{.2cm} B & 4 & 6 & 5 & 3 & 3 & 1 & 5 & 2 & 3 & 9 \\ \hline \end{array} \)
Tabla 20: Datos del Ejercicio Guiado 8 (.docx)
Contrastar, considerando un nivel de significación del 5%, si los tiempos medianos de ambas cajeras pueden asumirse iguales.
Solución:
Comenzamos creando el archivo de datos de ventas de las dos cajeras:

Tabla 28: Datos del Ejercicio Guiado 8
A continuación, vamos a plantear el contraste que se debe resolver
\( \left \{ \begin{array}{c} H_0 \equiv Me_A- Me_B = 0 \\ H_1 \equiv Me_A- Me_B \neq 0 \end{array}\right. \)
Expresión 46: Contraste de hipótesis para diferencias de medianas
Para resolver este contraste debemos tener en cuenta que los datos proceden de muestras independientes, que el valor de la diferencia entre las medianas que se pretende comprobar es 0 y que la hipótesis alternativa del contraste es del tipo “distinto de”.
En primer lugar, cargamos el fichero seleccionando: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra la siguiente ventana en la cual vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Cajeras. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Pulsamos Aceptar y se muestra una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos
Para resolver el contraste planteado, seleccionamos en el menú: Estadísticos/ Test no paramétricos/Test de Wilcoxon para dos muestras…
Se muestras la siguiente ventana en la que tenemos dos pestañas:
- En Datos tenemos que realizar dos selecciones: por un lado, elegir la variable “Cajera” en la ventana de Grupos para que las comparaciones las haga entre las dos cajeras, y en la ventana Variable explicada seleccionamos la variable “Frecuencia” dónde aparecían los tiempos de cada cajera por cada uno de los 10 clientes.
- En la pestaña Opciones, las opciones que vienen seleccionadas por defecto son las que necesitamos para resolver nuestro problema, excepto el Tipo de prueba. Si dejamos la opción “Por defecto” nos aplica el corrector por continuidad que, en nuestro caso, no vamos a aplicar. Por lo tanto, seleccionamos la opción “Exacto” y pulsamos Aceptar.
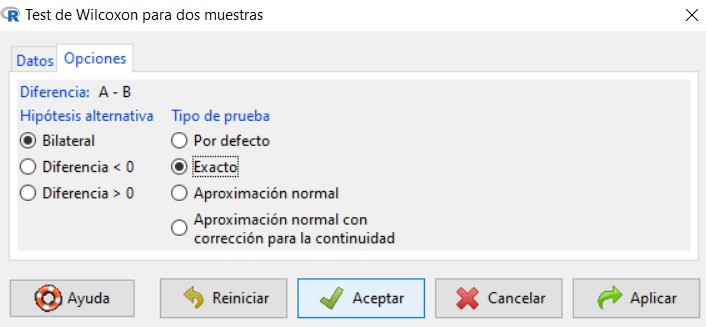
En la ventana de resultados nos aparece la siguiente información:
Wilcoxon rank sum test
data: Frecuencia by Cajera
W = 61.5, p-value = 0.3768
alternative hypothesis: true location shift is not equal to 0
En este caso, el p-valor asociado al contraste es 0.3768. Como este p-valor es mayor que 0.05 no se puede rechazar la hipótesis nula, considerando un nivel de significación del 5%. Por tanto, concluimos que las medianas de los tiempos de ambas cajeras pueden asumirse iguales.
Ejercicio Guiado 9 (Resuelto)
En una clínica se pretende comprobar la eficacia de un tratamiento de pérdida de peso. Para ello, se realiza un estudio a 10 voluntarios, y se registra el peso antes y después del tratamiento. Los resultados son los siguientes:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Antes & 65 & 60.5 & 89.2 & 74.5 & 68.9 & 77.3 & 59.8 & 65 & 98.4 & 106 \\ \hline Despues & 64.5 & 55 & 83.6 & 73 & 64.8 & 75.1 & 56 & 60.3 & 90.7 & 94 \\ \hline \end{array} \)
Tabla 21: Datos del Ejercicio Guiado 9 (.docx)
Suponiendo un nivel de significación del 5%, ¿Puede suponerse efectivo el tratamiento?
Solución:
Comenzamos creando el archivo de datos con la siguiente estructura:
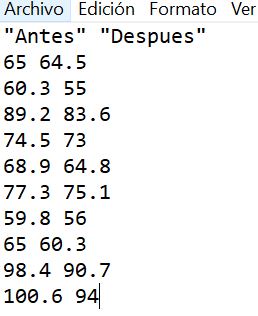 Tabla 29: Datos del Ejercicio Guiado 9
Tabla 29: Datos del Ejercicio Guiado 9
El contraste que se debe resolver es el siguiente
\( \left \{ \begin{array}{c} H_0 \equiv Me_{Antes}= Me_{Despues} \\ H_1 \equiv Me_{Antes} > Me_{Despues} \end{array}\right. \)
Expresión 47: Contraste de Hipótesis del Ejercicio Guiado 9
Para resolver este contraste debemos tener en cuenta que los datos proceden de muestras pareadas y que la hipótesis alternativa es unilateral del tipo “mayor que”.
En primer lugar, cargamos el fichero seleccionando: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra una ventana en la que vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Tratamiento. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Al pulsar Aceptar se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.
Para resolver el contraste planteado, seleccionamos en el menú: Estadísticos/ Test no paramétricos/Test de Wilcoxon para muestras pareadas…
Se muestra la siguiente ventana en la que tenemos dos pestañas:
- En Datos tenemos que realizar dos selecciones: por un lado, elegir la variable que nos indica el peso antes del tratamiento “Antes” en la ventana Primera variable, y la que nos indica el peso después del tratamiento “Después” en la ventana Segunda variable.

- En la pestaña Opciones, necesitamos seleccionar la Hipótesis alternativa mayor que (>), en Tipo de prueba seleccionamos la opción “Exacto” para que no nos aplique el corrector por continuidad y pulsamos Aceptar.
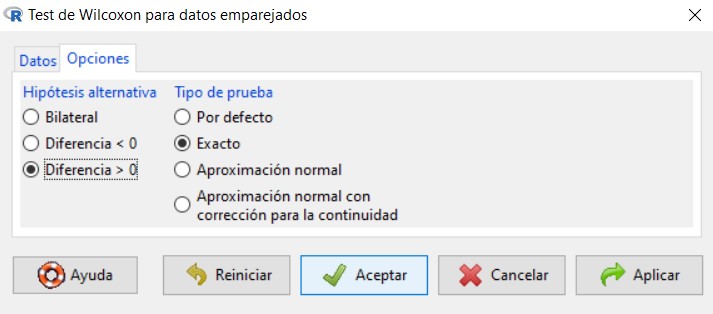
En la ventana de resultados nos aparece la siguiente información:
Wilcoxon signed rank exact test
data: Antes and Despues
V = 55, p-value = 0.0009766
alternative hypothesis: true location shift is greater than 0
En este ejemplo, el p-valor asociado al contraste es 0.0009766, inferior a 0.05, por lo que se rechaza la hipótesis nula considerando un nivel de significación del 5%. Esto quiere decir que el tratamiento utilizado es efectivo para reducir el peso en los pacientes.
Ejercicios Propuestos
Ejercicio Propuesto1
En un proyecto de clase se ha construido un dado dodecaédrico (12 caras). Para comprobar si el dado está bien construido, lo lanzamos 970 veces obteniendo los siguientes resultados que se muestran en la tabla.
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x_{i} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ \hline n_{i} & 75 & 20 & 68 & 129 & 98 & 156 & 35 & 28 & 87 & 102 & 73 & 99 \\ \hline \end{array} \)
Tabla 27: Datos del Ejercicio Propuesto 2(.docx)
Contrastar la hipótesis de que el dado está bien construido.
Ejercicio Propuesto 2
En Andalucía se quiere contrastar la independencia global entre las variables sexo y utilización de instalaciones deportivas de los municipios de la Comunidad. Para ello, se toma una muestra de 854 individuos cuyas observaciones figuran en la siguiente tabla
\( \begin{array} {|c|c|c|} \hline Sexo/Usuario & SI & NO \\ \hline Hombre & 238 & 194 \\ \hline Mujer & 190 & 232 \\ \hline \end{array} \)
Tabla 29: Datos del Ejercicio propuesto 2(.docx)
Considerando un nivel de significación del 5%, estudia si las dos variables si las dos variables están relacionadas o si, por el contrario, son independientes.
Ejercicio Propuesto 3
El portavoz del gobierno español ha dicho que más de la mitad de la población está de acuerdo con la aplicación del artículo 155 en una comunidad autónoma rebelde. Una televisión independiente (que no independentista) decide realizar una encuesta. De 288 personas encuestadas, 155 son favorables a la aplicación del artículo 155. ¿Ponen en duda estos resultados la publicidad del gobierno?
Ejercicio Propuesto 4
Se realiza un estudio sobre el tiempo de duración de los efectos secundarios tras la administración de un medicamento. Se ha observado una muestra de 10 pacientes y se ha anotado el tiempo de duración de los efectos secundarios en días: 3; 7; 5; 10; 14; 13; 7; 2; 9; 14. A un nivel de significación del 5%, ¿se puede considerar aleatoriedad en la muestra?
Ejercicio Propuesto 5
Los pesos en Kg de 10 niños de una clase de primaria han sido los siguientes: 20.81, 17.30, 24.20, 17.14, 19.29, 18.79, 24.73, 19.26, 25.74, 24.65. ¿Puede suponerse, a un nivel de significación del 5%, que dichos pesos se ajustan a una distribución normal de media 21 y desviación típica 3?
Ejercicio Propuesto 6
Se realiza un estudio para observar el tiempo que hacen efecto dos medicamentos distintos que se utilizan para tratar la misma dolencia. Para ello, se observa el número de horas que tarda en desaparecer su efecto tras su consumo en 10 pacientes:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Medicamento \hspace{.2cm} A & 8 & 6 & 6 & 5 & 7 & 9 & 7 & 5 & 6 & 6 \\ \hline Medicamento \hspace{.2cm} B & 4 & 6 & 5 & 3 & 3 & 1 & 5 & 2 & 3 & 4 \\ \hline \end{array} \)
Tabla 30: Datos del Ejercicio Propuesto 6(.docx)
Contrastar, considerando un nivel de significación del 5%, si los tiempos de efecto medianos de ambos medicamentos pueden asumirse iguales.
Ejercicio Propuesto 7
Los pacientes ancianos intervenidos de cadera, tienden a perder capacidad de velocidad de respuesta a determinados estímulos motores. Por eso, se ha desarrollado un programa que pretende desarrollar tal velocidad. La forma de valorar el programa es comparar la velocidad de respuesta antes y después de una semana de la aplicación de tal programa. Los datos que siguen a continuación corresponden a 9 pacientes a los que se les midió la velocidad de respuesta antes y al cabo de una semana del tratamiento.
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|} \hline Antes & 103 & 112 & 99 & 98 & 116 & 100 & 93 & 108 & 121 \\ \hline Despues & 96 & 93 & 90 & 81 & 100 & 101 & 90 & 93 & 98 \\ \hline \end{array} \)
Tabla 31: Datos del Ejercicio Propuesto 7 (.docx)
Suponiendo un nivel de significación del 5%, ¿Qué se puede decir del programa?
Ejercicio Propuesto8
En la tabla siguiente se muestran los salarios mensuales en euros de 10 trabajadores de Madrid y Barcelona.
\( \begin{array} {|c|c|c|} \hline Trabajador & Ciudad & Salario \\ \hline 1 & Madrid & 1800 \\ \hline 2 & Madrid & 2000 \\ \hline 3 & Barcelona & 2100 \\ \hline 4 & Madrid & 2300 \\ \hline 5 & Barcelona & 1900 \\ \hline 6 & Barcelona & 2500 \\ \hline 7 & Madrid & 1900 \\ \hline 8 & Madrid & 2300 \\ \hline 9 & Madrid & 2500 \\ \hline 10 & Barcelona & 1800 \\ \hline \end{array} \)
Tabla 32 : Datos del Ejercicio Propuesto 8(.txt)
Se pide:
a) Realizar un contraste de hipótesis al 89% de confianza para ver si el salario medio se puede considerar igual a 1500 euros o menor.
b) Realizar un contraste a un nivel del 90% con el objetivo de ver si hay diferencias significativas entre los salarios medios de ambas ciudades.
Contrastar si la proporción de trabajadores en Barcelona es igual a 0.5 con un nivel de confianza 90%
Ejercicio Propuesto 1(Resuelto)
En un proyecto de clase se ha construido un dado dodecaédrico (12 caras). Para comprobar si el dado está bien construido, lo lanzamos 970 veces obteniendo los siguientes resultados que se muestran en la tabla.
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x_{i} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ \hline n_{i} & 75 & 20 & 68 & 129 & 98 & 156 & 35 & 28 & 87 & 102 & 73 & 99 \\ \hline \end{array} \)
Tabla 28: Datos del Ejercicio Propuesto 1(.docx)
Contrastar la hipótesis de que el dado está bien construido.
Solución
counts:
P
1 2 3 4 5 6 7 8 9 10 11 12
75 20 68 129 98 156 35 28 87 102 73 99
percentages:
P
1 2 3 4 5 6 7 8 9 10 11 12
7.73 2.06 7.01 13.30 10.10 16.08 3.61 2.89 8.97 10.52 7.53 10.21
Chi-squared test for given probabilities
data: .Table
X-squared = 221.86, df = 11, p-value < 2.2e-16
Solución del Ejercicio propuesto 1
Ejercicio Propuesto 2 (Resuelto)
En Andalucía se quiere contrastar la independencia global entre las variables sexo y utilización de instalaciones deportivas de los municipios de la Comunidad. Para ello, se toma una muestra de 854 individuos cuyas observaciones figuran en la siguiente tabla
\( \begin{array} {|c|c|c|} \hline Sexo/Usuario & SI & NO \\ \hline Hombre & 238 & 194 \\ \hline Mujer & 190 & 232 \\ \hline \end{array} \)
Tabla 29: Datos del Ejercicio propuesto 2(.docx)
Considerando un nivel de significación del 5%, estudia si las dos variables si las dos variables están relacionadas o si, por el contrario, son independientes.
Solución
Frequency table:
Q
P No Si
Hombre 194 238
Mujer 232 190
Pearson’s Chi-squared test
data: .Table
X-squared = 8.6569, df = 1, p-value = 0.003258
Solución del Ejercicio propuesto 2
Ejercicio Propuesto 3 (Resuelto)
El portavoz del gobierno español ha dicho que más de la mitad de la población está de acuerdo con la aplicación del artículo 155 en una comunidad autónoma rebelde. Una televisión independiente (que no independentista) decide realizar una encuesta. De 288 personas encuestadas, 155 son favorables a la aplicación del artículo 155. ¿Ponen en duda estos resultados la publicidad del gobierno?
Solución
Frequency counts (test is for first level):
P
A favor En contra
155 133
Exact binomial test
data: rbind(.Table)
number of successes = 155, number of trials = 288, p-value = 0.9124
alternative hypothesis: true probability of success is less than 0.5
95 percent confidence interval:
0.0000000 0.5877884
sample estimates:
probability of success
0.5381944
Solución del Ejercicio propuesto 3
Ejercicio Propuesto 4 (Resuelto)
Se realiza un estudio sobre el tiempo de duración de los efectos secundarios tras la administración de un medicamento. Se ha observado una muestra de 10 pacientes y se ha anotado el tiempo de duración de los efectos secundarios en días: 3; 7; 5; 10; 14; 13; 7; 2; 9; 14. A un nivel de significación del 5%, ¿se puede considerar aleatoriedad en la muestra?
Solución
Runs Test
data: Ejemplo_Efectos$Tiempo
statistic = -1.3416, runs = 4, n1 = 5, n2 = 5, n = 10, p-value = 0.1797
alternative hypothesis: nonrandomness
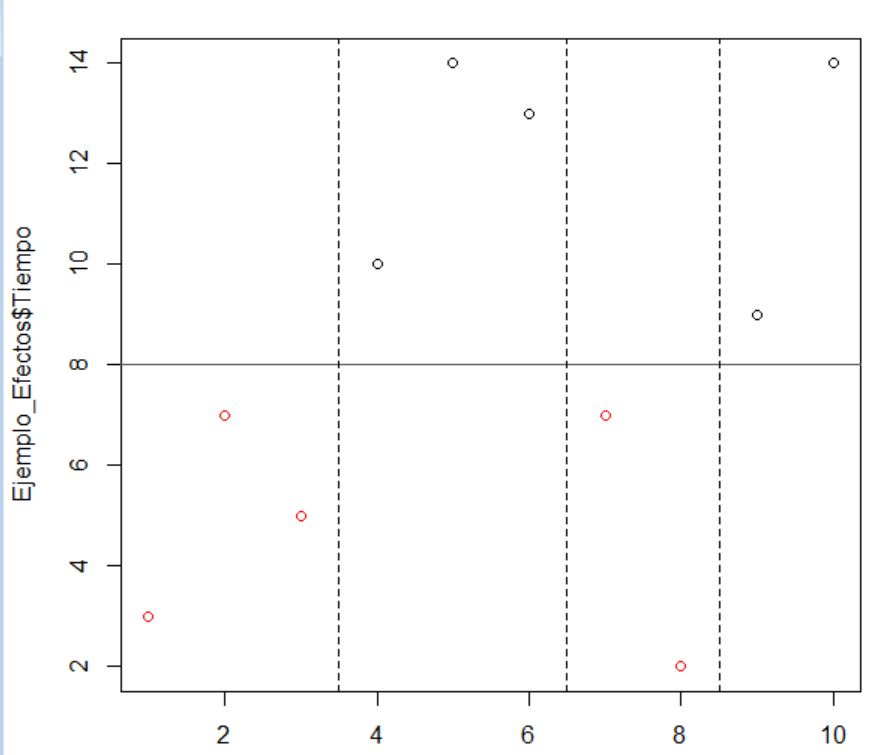
Solución del Ejercicio propuesto 4
Ejercicio Propuesto 5 (Resuelto)
Los pesos en Kg de 10 niños de una clase de primaria han sido los siguientes: 20.81, 17.30, 24.20, 17.14, 19.29, 18.79, 24.73, 19.26, 25.74, 24.65. ¿Puede suponerse, a un nivel de significación del 5%, que dichos pesos se ajustan a una distribución normal de media 21 y desviación típica 3?
Solución
One-sample Kolmogorov-Smirnov test
data: Ejemplo_Pesos$Pesos
D = 0.25694, p-value = 0.4498
alternative hypothesis: two-sided
Solución del Ejercicio propuesto 5
Ejercicio Propuesto 6 (Resuelto)
Se realiza un estudio para observar el tiempo que hacen efecto dos medicamentos distintos que se utilizan para tratar la misma dolencia. Para ello, se observa el número de horas que tarda en desaparecer su efecto tras su consumo en 10 pacientes:
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|c|} \hline Medicamento \hspace{.2cm} A & 8 & 6 & 6 & 5 & 7 & 9 & 7 & 5 & 6 & 6 \\ \hline Medicamento \hspace{.2cm} B & 4 & 6 & 5 & 3 & 3 & 1 & 5 & 2 & 3 & 4 \\ \hline \end{array} \)
Tabla 30: Datos del Ejercicio Propuesto 6(.docx)
Contrastar, considerando un nivel de significación del 5%, si los tiempos de efecto medianos de ambos medicamentos pueden asumirse iguales.
Solución
Wilcoxon rank sum test
data: Frecuencia by Medicamento
W = 94, p-value = 0.0007461
alternative hypothesis: true location shift is not equal to 0
Solución del Ejercicio propuesto 6
Ejercicio Propuesto 7 (Resuelto)
Los pacientes ancianos intervenidos de cadera, tienden a perder capacidad de velocidad de respuesta a determinados estímulos motores. Por eso, se ha desarrollado un programa que pretende desarrollar tal velocidad. La forma de valorar el programa es comparar la velocidad de respuesta antes y después de una semana de la aplicación de tal programa. Los datos que siguen a continuación corresponden a 9 pacientes a los que se les midió la velocidad de respuesta antes y al cabo de una semana del tratamiento.
\( \begin{array} {|c|c|c|c|c|c|c|c|c|c|} \hline Antes & 103 & 112 & 99 & 98 & 116 & 100 & 93 & 108 & 121 \\ \hline Despues & 96 & 93 & 90 & 81 & 100 & 101 & 90 & 93 & 98 \\ \hline \end{array} \)
Tabla 31: Datos del Ejercicio Propuesto 7 (.docx)
Suponiendo un nivel de significación del 5%, ¿Qué se puede decir del programa?
Solución
Wilcoxon signed rank exact test
data: Antes and Despues
V = 44, p-value = 0.003906
alternative hypothesis: true location shift is greater than 0
Solución del Ejercicio propuesto 7
Ejercicio Propuesto 8 (Resuelto)
En la tabla siguiente se muestran los salarios mensuales en euros de 10 trabajadores de Madrid y Barcelona.
\( \begin{array} {|c|c|c|} \hline Trabajador & Ciudad & Salario \\ \hline 1 & Madrid & 1800 \\ \hline 2 & Madrid & 2000 \\ \hline 3 & Barcelona & 2100 \\ \hline 4 & Madrid & 2300 \\ \hline 5 & Barcelona & 1900 \\ \hline 6 & Barcelona & 2500 \\ \hline 7 & Madrid & 1900 \\ \hline 8 & Madrid & 2300 \\ \hline 9 & Madrid & 2500 \\ \hline 10 & Barcelona & 1800 \\ \hline \end{array} \)
Tabla 32 : Datos del Ejercicio Propuesto 8(.txt)
Se pide:
a) Realizar un contraste de hipótesis al 89% de confianza para ver si el salario medio se puede considerar igual a 1500 euros o menor.
b) Realizar un contraste a un nivel del 90% con el objetivo de ver si hay diferencias significativas entre los salarios medios de ambas ciudades.
c) Contrastar si la proporción de trabajadores en Barcelona es igual a 0.5 con un nivel de confianza 90%
Solución
a)
One Sample t-test
data: Salario
t = 7.0752, df = 9, p-value = 1
alternative hypothesis: true mean is less than 1500
89 percent confidence interval:
-Inf 2223.65
sample estimates:
mean of x
2110
b)
F test to compare two variances
data: Salario by Ciudad
F = 1.2835, num df = 3, denom df = 5, p-value = 0.7512
alternative hypothesis: true ratio of variances is not equal to 1
90 percent confidence interval:
0.2372666 11.5686088
sample estimates:
ratio of variances
1.283482
Two Sample t-test
data: Salario by Ciudad
t = -0.31443, df = 8, p-value = 0.7612
alternative hypothesis: true difference in means between group Barcelona and group Madrid is not equal to 0
90 percent confidence interval:
-403.3204 286.6537
sample estimates:
mean in group Barcelona mean in group Madrid
2075.000 2133.333
c)
Frequency counts (test is for first level):
Ciudad
Barcelona Madrid
4 6
1-sample proportions test without continuity correction
data: rbind(.Table), null probability 0.5
X-squared = 0.4, df = 1, p-value = 0.5271
alternative hypothesis: true p is not equal to 0.5
90 percent confidence interval:
0.1942270 0.6483614
sample estimates:
p
0.4
Solución del Ejercicio propuesto 8
APÉNDICE
Introducción al Análisis de datos categóricos: Tablas de Contingencia
Las variables cualitativas o categóricas son aquellas que expresan una cualidad no numérica de los individuos. Un buen ejemplo de este tipo de variables es el color de ojos. Los posibles valores que puede tomar una variable cualitativa reciben el nombre de modalidades o categorías. Siguiendo con el ejemplo del color de ojos, las categorías de esta variable son “Azul”, “Marrón”, “Negro” y “Verde”.
Existen distintos tipos de variables cualitativas:
- Variables cualitativas nominales. Este tipo de variables se caracteriza por la inexistencia de un orden específico entre sus categorías, de manera que dos personas distintas pueden establecer una ordenación diferente de las mismas. Por ejemplo, el género de una persona es una variable cualitativa nominal, pues sus dos categorías (“Hombre” y “Mujer”) pueden ordenarse indistintamente como “Hombre”-“Mujer” o como “Mujer”-“Hombre”.
- Variables cualitativas ordinales. A diferencia de las anteriores, en las variables cualitativas ordinales sí existe un orden predeterminado entre las modalidades basado en alguna característica intrínseca de la propia variable. La opinión de una persona sobre un restaurante es un ejemplo de variable cualitativa ordinal, ya que sus categorías pueden ordenarse de la menos favorable a la más favorable (“Malo”, “Regular” y “Bueno”) o viceversa. Otros ejemplos pueden ser: el rango militar, la clase social, el nivel de estudios
- Variables cualitativas por intervalo. Son aquellas que surgen de la categorización de variables inicialmente cuantitativas. Estas variables pueden tratarse como ordinales pero en éstas se pueden calcular distancias numéricas entre dos niveles de la escala ordinal. (Ejemplos: el sueldo, la edad, los días del mes, el nivel de presión sanguínea. Son ejemplos de variables que se pueden agrupar por intervalos).
El conjunto de técnicas estadísticas específicas para el estudio de la asociación entre variables cualitativas recibe el nombre de Análisis de Datos Cualitativos o Categóricos.
Tablas de Contingencia
Una tabla de contingencia es una tabla de frecuencias bidimensional en la que se recoge el número de individuos que presentan simultáneamente cada una de las combinaciones de las modalidades de dos variables cualitativas.
Si consideramos dos variables cualitativas, X e Y, con k y p modalidades, respectivamente, la tabla de contingencia asociada sería la siguiente:
\( \begin{array}{|c|c|c|c|c|} \hline X/ Y & X_1 & X_2 & \cdots & X_k \\ \hline Y_1 & n_{11} & n_{12} & \cdots & n_{1k} \\ \hline Y_2 & n_{21} & n_{22} & \cdots & n_{2k} \\ \hline \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline Y_p & n_{p1} & n_{p2} & \cdots & n_{pk} \\ \hline \end{array} \)
Tabla 32: Tabla de contingencia
En esta tabla, \( n_{ij} \) representa el número de individuos que presentan simultáneamente la modalidad i de la variable X y la modalidad j de la variable Y, y se denomina, habitualmente, frecuencia absoluta observada.
Cuando se estudian dos variables cualitativas resulta interesante analizar si existe, o no, algún tipo de relación o asociación entre ellas, es decir, si ambas variables son dependientes o no lo son.
El estudio de la dependencia (o, equivalentemente, de la independencia) entre dos variables cualitativas pasa por resolver el siguiente contraste de hipótesis:
\( H_0 \equiv \) X e Y son independientes
\( H_1 \equiv \) X e Y no son independientes (son dependientes)
Para resolver este contraste de hipótesis se debe calcular el siguiente estadístico de contraste:
\( \chi^{2}_{exp} = \displaystyle \sum_{i=1}^{k} \displaystyle \sum_{j=1}^{p} \displaystyle \frac { (n_{ij} – e_ {íj} )^{2}} {e_{ij}} \)
Expresión 48: Estadístico de contraste Chi Cuadrado
donde
\( e_{ij} = \displaystyle \frac {n_{i.} \times n_{.j}} {n} \)
recibe el nombre de frecuencia absoluta esperada ya que es el número de individuos que se esperaría obtener en cada casilla de la tabla de contingencia si se cumpliera el supuesto de independencia entre las dos variables cualitativas.
Bajo la hipótesis nula, \( \chi^{2}_{exp} \) se distribuye según una \( \chi^{2}_{(k-1) \times (p-1)} \), siendo k y p el número de filas y columnas, respectivamente, de la tabla de contingencia.
Cuando se rechaza la hipótesis nula en el contraste de independencia y, consecuentemente, se concluye que existe un cierto grado de asociación entre las variables, puede resultar interesante estudiar la intensidad de tal asociación.
Existen diversas medidas para determinar la asociación entre las dos variables. A la hora de elegir una medida hay que tener en cuenta el tipo de las variables.
Medidas de asociación de variables categóricas
Medidas de asociación de variables nominales
-
Coeficiente \( \phi \)
\( \phi \displaystyle \sqrt { \displaystyle \frac { \chi^{2}} {n} } \)
Expresión 49: Coeficiente \( \phi \)
En las tablas de contingencia 2 x 2, el coeficiente \( \phi \) (Φ) oscila entre 0 y 1.
- Si \( \phi \) = 0 , las variables son independientes y
- Si \( \phi \) = 1, existe una asociación perfecta entre las variables.
- Si alguna de las dos variables tiene más de dos niveles, este coeficiente puede tomar un valor superior a 1.
-
Coeficiente C de contingencia
\( C \displaystyle \sqrt { \displaystyle \frac { \chi^{2}} {\chi^{2} + n} } \)
Expresión 50: Coeficiente C de contingencia
El coeficiente de contingencia se utiliza cuando las dos variables tienen el mismo número de niveles.
El coeficiente de contingencia oscila
- entre 0 y \( \sqrt {2/2} \) en tablas de contingencia \( 2 \times 2 \) y
- entre 0 y \( \displaystyle \sqrt {\displaystyle \frac {k-1}{k} } \).
- Si \( C = 0 \), las variables son independientes y cuanto mayor sea el valor de \( C \), mayor será el grado de asociación entre las variables.
-
Coeficiente V de Cramer.
El coeficiente \( V \) de Cramer es una modificación del coeficiente \( \phi \) y se calcula como
\( V = \displaystyle \sqrt { \displaystyle \frac { \chi^{2}} {n \times \min (k-1, m-1)} } \)
Expresión 51: Coeficiente V de Cramer
En las tablas de contingencia \( 2 \times k \) o \( p \times 2 \) el coeficiente \( \phi \) y el coeficiente \( V \) de Cramer coinciden.
El coeficiente \( V \) de Cramer oscila entre 0 y 1. Si \( V = 0 \), las variables son independientes y si \( V = 1 \), existe una asociación perfecta entre las variables.
-
Coeficiente Lambda
Al contrario que las medidas anteriores, el coeficiente lambda no depende del valor del estadístico \( \chi^{2} \).
Cuando la variable Y actúa como variable dependiente y la variable X actúa como variable independiente, el coeficiente lambda mide la capacidad de X para predecir Y. En este caso, se calcula como
\( \lambda_{Y} = \displaystyle \frac { \sum_{i} máx_{j}n_{ij} – máx_j n{.j}}{n- máx_jn_{ij}} \)
Expresión 52: Coeficiente Lamdda (X predice Y)
Cuando la variable X actúa como variable dependiente y la variable Y actúa como variable independiente, el coeficiente lambda mide la capacidad de Y para predecir X. En este caso, se calcula como
\( \lambda_{X} = \displaystyle \frac { \sum_{j} máx_{i}n_{ij} – máx_i n{i.}}{n- máx_i n_{ij}} \)
Expresión 53: Coeficiente Lamdda (Y predice X)
Los valores del coeficiente lambda están comprendidos entre 0 y 1 para tablas \( p \times q \), con \( p, q \geq 2 \).
Valores próximos a 0 implican baja asociación y valores próximos a 1 denotan fuerte asociación. Sin embargo un valor de 0 no implica independencia entre los atributos.
Dos variables son independientes cuando \( \lambda = 0 \), pero \( \lambda = 0 \) no implica independencia estadística.
Medidas de asociación de variables ordinales
Algunas de las medidas para calcular el grado de asociación entre variables de tipo ordinal son:
-
Coeficiente gamma de Goodman y Kruskal
El coeficiente gamma se calcula como
\( \gamma = \displaystyle \frac { C-D}{C+D} \)
Expresión 54: Coeficiente gamma de Goodman y Kruskal
siendo
- C el número de concordancias, es decir, el número de veces en las que los dos valores de un caso en ambas variables son mayores o menores que los del caso precedente.
- D el número de discordancias, es decir, el número de veces en las que el valor de una de las variables es mayor que el valor precedente de dicha variable mientras que el valor de la otra variable es menor que el valor precedente de dicha variable (o viceversa).
-
Coeficiente d de Somers
Existen diversas versiones del coeficiente d de Somers, dependiendo de cuál de las dos variables se considera dependiente y cuál se considera independiente.
Cuando la variable independiente es Y
\( d_X = \displaystyle \frac {C-D}{C+D+E_X} \)
Expresión 55: Coeficiente de de Somers . La variable Y es independiente
siendo \( E_X \) el número de empates en la variable X, es decir, el número de veces en los que los valores de dos casos consecutivos coinciden en la variable X, pero no en la variable Y.
Cuando la variable independiente es X
\( d_Y = \displaystyle \frac {C-D}{C+D+E_Y} \)
Expresión 56: Coeficiente de Somers . La variable X es independiente
siendo \( E_Y \) el número de empates en la variable Y, es decir, el número de veces en los que los valores de dos casos consecutivos coinciden en la variable Y, pero no en la variable Y.
-
Coeficiente tau-b de Kendall
Este coeficiente se calcula como
\( \tau_b = \displaystyle \frac {C-D}{\displaystyle \sqrt {(C+D+E_X) (C+D+E_Y)}} \)
Expresión 57: Coeficiente tau-b de Kendall
-
Coeficiente tau-c de Kendall
Este coeficiente se calcula como
\( \tau_c = \displaystyle \frac {2m (C-D)}{n^{2} \times (m-1)} \)
Expresión 58: Coeficiente tau-c de Kendall
Las cuatro medidas presentadas en este apartando oscilan entre -1 y 1 y su interpretación es muy similar.
- Si la medida es igual a 0, las dos variables son independientes.
- Si la medida es igual a 1, existe una asociación perfecta y positiva entre las variables y
- Si la medida es igual a -1, la asociación también es perfecta, pero negativa.
Supuesto Práctico 18
Creamos festival.txt que contiene información sobre el género (Hombre o Mujer) y la intención de asistir o no a un festival de música de 20 individuos.
\( \begin{array}{||c|c|c||} \hline Sexo / Asistencia & SI & NO \\ \hline Hombre & 5 & 3 \\ \hline Mujer & 8 & 4 \\ \hline \end{array} \)
Tabla 33: Datos del Supuesto Práctico 18 (.docx)
Calcula la tabla de contingencia asociada y determina, a un nivel de significación del 5%, si existe algún tipo de asociación entre ambas variables.
Solución
El primer paso consiste en crear el fichero de datos de la siguiente forma:

Tabla 34: Datos del Supuesto Práctico 18 (.txt)
A continuación, cargamos el fichero de datos: Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra la siguiente ventana en la cual vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Festival. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Pulsamos Aceptar se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.
El contraste de hipótesis que nos permitirá decidir sobre la dependencia o independencia del género y la intención de asistir al festival de música es el siguiente:
\( H_0 \equiv \) El género y la intención de asistir al festival son independientes
\( H_1 \equiv \) El género y la intención de asistir al festival son dependientes
Para resolver el contraste con R-Commander se usa la opción:
Estadísticos/Tablas de contingencia/Tabla de doble entrada
Se muestra una ventana con dos pestañas:
- En la pestaña Datos selecionamos la variable “Sexo” por filas y “Asistir” por columnas.
- En la pestaña Estadísticos seleccionamos el Test de independencia Chi-cuadrado e imprimimos las frecuencias esperadas.
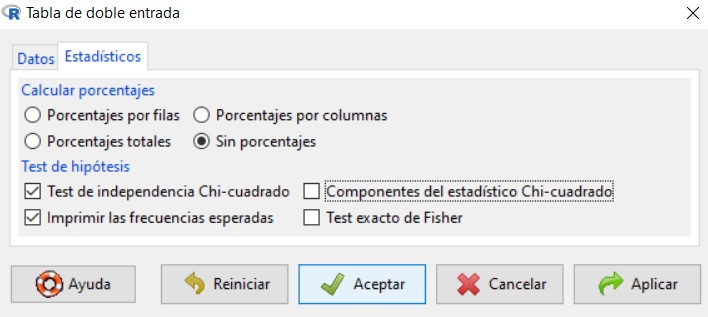
Pulsamos Aceptar.
En la ventana de resultados nos aparece la siguiente información:
Frequency table:
Asistir
Sexo No Si
Hombre 3 5
Mujer 4 8
Pearson’s Chi-squared test
data: .Table
X-squared = 0.03663, df = 1, p-value = 0.8482
Expected counts:
Asistir
Sexo No Si
Hombre 2.8 5.2
Mujer 4.2 7.8
En primer lugar podemos observar la tabla de contingencia con la variable “Sexo” por filas y “Asistir” por columnas. A continuación nos aparece el estadístico de contraste del test Chi-cuadrado (X-squared), los grados de libertad asociados a este contraste (df) y el p-valor (p-value). Para finalizar, nos aparece la tabla de contingencia con las frecuencias esperadas.
En este caso, el valor del estadístico de contraste es 0,03663 con un p-valor asociado de 0,8482. Como este p-valor es superior al nivel de significación (0,05), no podemos rechazar la hipótesis nula, por lo que concluimos que las variables género e intención de asistir al festival de música son independientes o, dicho de otra forma, el género no influye en la intención de asistir al festival.
Si observamos la tabla de frecuencias esperadas, vemos que no se cumple una de las hipótesis del contraste de independencia. En concreto, la que dice que, como mucho, el 20% de los valores que se calculan pueden ser inferiores a 5.
Como se aprecia, 2 de los 4 valores esperados (es decir, el 50%) están por debajo de 5. Esto ocurre con frecuencia cuando se trabaja con muestras de tamaño reducido, como es nuestro caso. En estas situaciones, hay que interpretar los resultados con precaución.
Supuesto Práctico 19
Se realiza un estudio sobre las relaciones entre la opinión sobre la prohibición de fumar en lugares públicos y el hecho de ser fumador o no. Para ello, se seleccionan 350 personas, de las cuales 140 son fumadores.
\( \begin{array}{||c|cccc|c||} \hline & & & \hspace {-1cm} Opinión & & \\ \hline & Muy \hspace {.1cm} en & En & A & Muy \hspace {.1cm} a & \\ Fumador & contra & contra & favor & favor & Total \\ \hline Si & 60 & 50 & 20 & 10 & 140 \\ \hline No & 10 & 30 & 70 & 100 & 210 \\ \hline Total & 70 & 80 & 90 & 110 & 350 \\ \hline \end{array} \)
Tabla 35: Datos del Supuesto Práctico 19 (.docx)
Determinar, a través del test chi-cuadrado de independencia, considerando un nivel de significación del 5% si existe relación entre la condición de fumador y la opinión sobre la prohibición de fumar en sitios públicos.
Solución
En primer lugar para trabajar con R_Commander escribimos la siguiente sentencia en R
> library(Rcmdr)
Introducimos los datos en R-Commander. Para ello, creamos un fichero de texto como el que aparece en la Imagen

Tabla 36: Datos del Supuesto Práctico 19 (.txt)
Como puede verse, en la primera fila introducimos el nombre de las variables entre comillas y separados por un espacio. A continuación, en las siguientes filas se van introduciendo los datos que aparecen en la tabla. Hay que tener en cuenta que las modalidades de las variables cualitativas hay que escribirlas entre comillas.
A continuación, cargamos el fichero creado mediante las siguientes instrucciones:
Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra la siguiente ventana en la que introducimos el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Fumadores. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Una vez le damos a Aceptar se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

Para transformar la tabla de contingencia en un conjunto de datos (data.frame) con el que R-Commander pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script, seleccionar las tres a la vez y pulsar Ejecutar:
P<-rep(Ejemplo_Fumadores$Fumador,Ejemplo_Fumadores$Frecuencia)
Q<-rep(Ejemplo_Fumadores$Opinion,Ejemplo_Fumadores$Frecuencia)
Fumador_Opinion<-data.frame(P,Q)
Para visualizar el conjunto de datos en forma de lista deberemos pulsar en el botón Conjunto de datos y seleccionar el nuevo conjunto de datos creado, al que hemos llamado Fumador_Opinion (observar la tercera instrucción).

Observamos que en Conjunto de datos aparece Fumador_Opinion.
A continuación, planteamos el contraste a resolver:
\( H_0 \equiv \) La condicion de fumador y la opinión sobre la prohibición de fumar en espacios públicos son independientes
\( H_1 \equiv \) La condicion de fumador y la opinión sobre la prohibición de fumar en espacios públicos son dependientes
Y procedemos a resolverlo mediante la opción:
Estadísticos/Tablas de contingencia/Tabla de doble entrada
Se muestra la siguiente ventana, en la cual, si nos fijamos en la esquina superior izquierda, tenemos dos pestañas. En la pestaña Datos tenemos que seleccionar las variables que queremos que aparezcan tanto por filas (en nuestro caso, la variable P a la que hemos asignado si es fumador o no) como por columnas (seleccionamos la variable Q a la que hemos asignado la opinión).
En la pestaña Estadísticos tenemos la opción de incluir algún porcentaje en la tabla de doble entrada, aunque por defecto aparece sin porcentajes. En principio, lo vamos a dejar así. También aparece seleccionado el Test de independencia Chi-cuadrado, que es el que nos interesa. Por tanto, no modificamos ninguna de las opciones
Pulsamos Aceptar.
En la ventana de salida nos aparecen los siguientes resultados:
- En primer lugar, la tabla de doble entrada en la que se incluyen únicamente las frecuencias absolutas.
- A continuación nos aparece el estadístico de contraste del test (X-squared), los grados de libertad asociados al test (df) y el p-valor (p-value).
Frequency table:
Q
P A favor En contra Muy a favor Muy en contra
No 70 30 110 10
Si 20 50 10 60
Pearson’s Chi-squared test
data: .Table
X-squared = 141.01, df = 3, p-value < 2.2e-16
Como podemos ver, el estadístico de contraste, que sigue una distribución Chi-Cuadrado con 3 grados de libertad, toma el valor 141.01. El p-valor asociado al contraste es muy pequeño. Como este p-valor es menor que 0.05, se rechaza la hipótesis nula y se concluye que existe cierta asociación entre la condición de fumador y la opinión sobre la prohibición de fumar en espacios públicos.
Pasemos ahora a determinar la intensidad de dicha asociación. Para ello, y teniendo en cuenta que las dos variables que se están estudiando son de tipo nominal, calcularemos el coeficiente phi, el coeficiente C de contingencia, el coeficiente V de Cramer y los coeficientes lambda.
Para calcular los coeficientes de asociación debemos instalar y cargar el paquete DescTools. Para ello, nos vamos a la ventana RGui y seleccionamos en el menú:
Paquetes/Instalar paquetes(s)…
A continuación se muestra la ventana Secure CRANmirros dónde seleccionamos Spain (Madrid) y pulsamos OK
En la ventana Packages seleccionamos Desc Tools y pulsamos OK
Ya tenemos instalado el paquete, pero ahora hay que cargarlo para poder trabajar con él. En el menú seleccionamos:
Paquetes/Cargar paquete…
En la ventana Select one que se abre, seleccionamos el paquete Desc Tools que acabamos de instalar y pulsamos Ok.
Para poder trabajar desde R-Commander con el paquete, en la ventana RScriptescribimos la instrucción
> library(DescTools)
La seleccionamos y pulsamos Ejecutar.
A continuación calculamos el coeficiente phi mediante la función Phi, que tiene un único argumento
Phi (x)
donde
- x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
En nuestro caso, escribiremos en R Script la instrucción siguiente
Phi(.Table)
Para ello, en primer lugar escribimos la siguiente instrucción en R Script
> .Table <- xtabs(~P+Q, data=Fumador_Opinion)
La seleccionamos y pulsamos Ejecutar. A continuación podemos calcular los coeficientes
> Phi(.Table)
[1] 0.6258575
El coeficiente de contingencia se obtiene mediante la función ContCoef, cuyo argumento es el mismo que el de la función Phi:
ContCoef (x)
donde
- x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
En este ejemplo concreto, el valor del coeficiente de contingencia se calcula del siguiente modo:
ContCoef(.Table)
y su valor aparecerá en la ventana de resultados.
> ContCoef(.Table)
[1] 0.5305215
Para obtener el coeficiente V de Cramer en R se utiliza la función CramerV, la cual, además de la tabla de contingencia, puede recibir como argumento opcional un nivel de confianza en cuyo caso calcula un intervalo de confianza para el coeficiente.
CramerV (x, conf.level = NA)
donde
- x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
- level es el valor del nivel de confianza a partir del cual se calcula un intervalo de confianza para el coeficiente.
El coeficiente V de Cramer para los datos de este ejemplo se obtiene escribiendo
CramerV(.Table, conf.level = 0.95)
lo que nos da como resultado
> CramerV(.Table, conf.level = 0.95)
Cramer V lwr.ci upr.ci
0.6258575 0.5176767 0.7250340
El valor de los 3 coeficientes sugiere una relación moderada-alta entre las dos variables objeto de estudio. Los valores de los extremos del intervalo de confianza para el coeficiente V de Cramer indican que dicho coeficiente es significativamente distinto de 0 (puesto que el 0 no es un valor del intervalo).
Por último, el coeficiente lambda se calcula en R con la función Lambda, que tiene los siguientes argumentos:
Lambda (x, direction = c(“symmetric”, “row”, “column”), conf.level = NA)
donde
- x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
- direction indica la versión del coeficiente que se calculará. Por defecto se calcula la versión simétrica del coeficiente (symmetric), en la que las dos variables desempeñan el mismo papel de manera que no se distingue entre variable dependiente y variable independiente. Si se selecciona el valor row para este argumento, la variable situada en las filas asume el papel de variable dependiente, mientras que si se selecciona el valor column, será la variable situada en las columnas la que ejerza el papel de variable dependiente.
- level es el valor del nivel de confianza a partir del cual se calcula un intervalo de confianza para el coeficiente.
En este ejemplo, para calcular el coeficiente lambda simétrico y los dos coeficientes lambda asimétricos escribimos en R Script las siguientes instrucciones respectivamente.
En este ejemplo, el coeficiente lambda simétrico y los dos coeficientes lambda asimétricos son los siguientes:
> Lambda(.Table, direction = c(“symmetric”), conf.level = 0.95)
lambda lwr.ci upr.ci
0.3157895 0.2391714 0.3924075
> Lambda(.Table, direction = c(“row”), conf.level = 0.95)
lambda lwr.ci upr.ci
0.5000000 0.3787587 0.6212413
> Lambda(.Table, direction = c(“column”), conf.level = 0.95)
lambda lwr.ci upr.ci
0.2083333 0.1475398 0.2691268
El valor del coeficiente lambda simétrico es 0.315. Un intervalo de confianza al 95% para este coeficiente es (0.239, 0.392). Esto indica que el coeficiente es significativo a un 5% de significación. Según este coeficiente, la asociación entre ambas variables es moderada-baja.
Cuando se considera como variable dependiente la situada en las filas (es decir, la condición de fumador), el valor del coeficiente lambda es 0.5. Esto se interpreta del siguiente modo: cuando se conoce la opinión del individuo, se reduce en un 50% la probabilidad de cometer un error al predecir la condición de fumador de dicho individuo. De forma similar, conocida la condición de fumador de un individuo se reduce en un 20.8% el error al predecir su opinión. Se concluye, por tanto, que la capacidad predictiva de la variable opinión sobre la variable fumador es mayor que a la inversa.
Supuesto Práctico 20
Se realiza un estudio sobre la práctica deportiva y la sensación de bienestar. Se desea saber si hay asociación entre ambas variables. La práctica deportiva se clasifica en poca, moderada, alta y muy alta y la sensación de bienestar se clasifica en poca, moderada y alta. Para dicho estudio se selecciona una muestra aleatoria de 500 sujetos. Los datos se muestran en la siguiente tabla:
\( \begin{array} {|c|ccc|} \hline & \hspace{2 cm}Sensación & \hspace{-2 cm} de \hspace{-1 cm} & bienestar \hspace{2 cm} \\ \hline \hline Práctica \hspace {.1cm} deportiva & Poca & Moderada & Alta \\ \hline Poca & 75 & 35 & 40 \\ \hline Moderada & 60 & 70 & 50 \\ \hline Alta & 20 & 30 & 40 \\ \hline Muy \hspace {.1cm} Alta & 15 & 25 & 40 \\ \hline \end{array} \)
Tabla 37: Datos del Supuesto Práctico 20 (.docx)
Realizar los contrastes necesarios (considerando un nivel de significación del 5%) y calcular e interpretar las medidas de asociación.
Solución
Recordar que tenemos que introducir en R la siguiente instrucción
> library(Rcmdr)
para poder trabajar con R_Commander
En primer lugar, vamos a introducir los datos en R-Commander. Para ello, creamos un fichero de texto como el que aparece en la Imagen

Tabla 38: Datos del Supuesto Práctico 20 (.txt)
Como puede verse, en la primera fila introducimos el nombre de las variables entre comillas y separados por un espacio. A continuación, en las siguientes filas se van introduciendo los datos que aparecen en la tabla. Hay que tener en cuenta que las modalidades de las variables cualitativas hay que escribirlas entre comillas.
A continuación, cargamos el fichero creado mediante las siguientes instrucciones:
Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra la siguiente ventana en la cual vamos a introducir el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Deporte. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Pulsamos Aceptar y se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos
Para transformar la tabla de contingencia en un conjunto de datos (data.frame) con elque R-Commander pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script, seleccionar las tres a la vez y darle a Ejecutar:
P<-rep(Ejemplo_Deporte$Practica,Ejemplo_Deporte$Frecuencia)
Q<-rep(Ejemplo_Deporte$Sensacion,Ejemplo_Deporte$Frecuencia)
Practica_Sensacion<-data.frame(P,Q)
Para visualizar el conjunto de datos en forma de lista deberemos pulsar en el botón Conjunto de datos y seleccionar el nuevo conjunto de datos creado, al que hemos llamado Practica_Sensacion (observar la tercera instrucción).
Pulsamos Aceptar
El contraste que debemos resolver es el siguiente:
\( H_0 \equiv \) La práctica deportiva y la sensación de bienestar son independientes
\( H_1 \equiv \) La práctica deportiva y la sensación de bienestar son dependientes
Y procedemos a resolverlo mediante la opción:
Estadísticos/Tablas de contingencia/Tabla de doble entrada
Se muestra la siguiente ventana que presenta dos pestañas. En la pestaña Datos tenemos que seleccionar las variables que queremos que aparezcan tanto por filas (en nuestro caso, la variable P a la que hemos asignado si realiza práctica deportiva) como por columnas (seleccionamos la variable Q a la que hemos asignado la sensación de bienestar).

En la pestaña Estadísticos tenemos la opción de incluir algún porcentaje en la tabla de doble entrada, aunque por defecto aparece sin porcentajes. En principio, lo vamos a dejar así. También aparece seleccionado el Test de independencia Chi-cuadrado, que es el que nos interesa. Por tanto, no modificamos ninguna de las opciones y le damos a Aceptar.
La ventana de salida muestra los siguientes resultados:
- En primer lugar, la tabla de doble entrada en la que se incluyen únicamente las frecuencias absolutas.
- A continuación nos aparece el estadístico de contraste del test (X-squared), los grados de libertad asociados al test (df) y el p-valor (p-value).
Frequency table:
Q
P Alta Moderada Poca
Alta 40 30 20
Moderada 50 70 60
Muy Alta 40 25 15
Poca 40 35 75
Pearson’s Chi-squared test
data: .Table
X-squared = 40.049, df = 6, p-value = 0.0000004455
Como podemos ver, el estadístico de contraste, que sigue una distribución Chi-Cuadrado con 6 grados de libertad, toma el valor 40.049. El p-valor asociado al contraste es muy pequeño. Como este p-valor es menor que 0.05, rechazamos la hipótesis de que la práctica deportiva y el nivel de bienestar sean variables independientes y se concluye que existe cierta asociación entre la práctica deportiva y el nivel de bienestar.
Tiene sentido, por tanto, cuantificar el grado de asociación entre ambas variables. Para cuantificarlo debemos tener presente que ambas variables son de tipo ordinal. Por tanto, calcularemos los 4 coeficientes de asociación que se han expuesto para este tipo de variables: gamma de Goodman y Kruskal, d de Somers, tau b de Kendall y tau c de Kendall.
Para calcular los coeficientes de asociación debemos instalar y cargar el paquete DescTools.
Para ello, en la ventana RGui y seleccionamos en el menú: Paquetes/Instalar paquetes(s)…
A continuación nos aparece la ventana Secure CRANmirros dónde seleccionamos Spain (Madrid).
En la ventana Packages seleccionamos Desc Tools y pulsamos OK.
Ya tenemos instalado el paquete, pero ahora hay que cargarlo para poder trabajar con él. En el menú seleccionamos: Paquetes/Cargar paquete…
Para poder trabajar desde R-Commander con el paquete, en la ventana RScript escribimos la instrucción
library(DescTools)
La seleccionamos y pulsamos Ejecutar.
Una vez hecho esto, podemos calcular el coeficiente gamma de Goodman y Kruskal a través de la función GoodmanKruskalGamma, que tiene los siguientes argumentos:
GoodmanKruskalGamma(x, conf.level = NA),
que tiene los siguientes argumentos:
- x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
- level es el valor del nivel de confianza a partir del cual se calcula un intervalo de confianza para el coeficiente.
Para ello, en primer lugar escribimos la siguiente instrucción en R Script
> Table <- xtabs(~P+Q, data=Practica_Sensacion)
La seleccionamos y pulsamos Ejecutar. A continuación podemos calcular los coeficientes
> GoodmanKruskalGamma(.Table, conf.level = 0.95)
gamma lwr.ci upr.ci
0.3053435 0.1645717 0.4461153
El valor del coeficiente gamma es de 0,305, lo que indica una asociación positiva y débil entre ambas variables. El intervalo de confianza para el coeficiente, a un nivel de confianza del 95% es (0,1645, 0,44611).
Para obtener los coeficientes d de Somers, se utiliza la función SomersDelta. Esta función tiene los siguientes argumentos:
SomersDelta(x, direction = c(“row”, “column”), conf.level =NA)
donde
- x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
- direction indica qué coeficiente de Somers se calcula. Por defecto, direction = “row”, lo que implica que la variable situada en las filas actúa como variable dependiente. Si se desea que la variable dependiente sea la situada en las columnas, basta con adjudicar el valor “column” a este argumento.
- level es el valor del nivel de confianza a partir del cual se calcula un intervalo de confianza para el coeficiente.
Para calcular los coeficientes d de Somers en nuestro caso escribiremos
> SomersDelta(.Table, direction =c(“row”), conf.level = 0.95)
somers lwr.ci upr.ci
0.16701461 0.08812176 0.24590746
> SomersDelta(.Table, direction = c(“column”), conf.level = 0.95)
somers lwr.ci upr.ci
0.2597403 0.1371380 0.3823425
Cuando la variable situada en las filas (práctica deportiva) actúa como dependiente, el valor del coeficiente es 0,1670, lo que indica una asociación positiva y baja entre las variables. Un intervalo de confianza al 95% para este coeficiente es (0,088, 0,2459).
Si la variable independiente es la situada en las columnas (sensación de bienestar), el valor del coeficiente es 0,2597, indicando, nuevamente una asociación positiva y baja entre las variables. En este caso, el intervalo de confianza para el coeficiente al 95% de confianza es (0,1371, 0,382).
Los coeficientes tau de Kendall (tau-b y tau-c) se calculan mediante las funciones KendallTauB y StuartTauC, respectivamente. Los parámetros de estas funciones son los mismos:
KendallTauB (x, conf.level = NA)
StuartTauC (x, conf.level = NA)
donde
- x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
- level es el valor del nivel de confianza a partir del cual se calcula un intervalo de confianza para el coeficiente.
Así, en nuestro ejemplo concreto, ambos coeficientes se calculan tal y como se indica a continuación:
> KendallTauB(.Table, conf.level = 0.95)
tau_b lwr.ci upr.ci
0.2082797 0.1102870 0.3062723
> StuartTauC (.Table, conf.level = 0.95)
tauc lwr.ci upr.ci
0.2469136 0.1297873 0.3640399
El valor del coeficiente tau-b de Kendall es 0,2082, con un intervalo de confianza al 95% de confianza de (0,1102, 0,3062). El coeficiente tau-c de Kendall toma un valor de 0,2469 y el intervalo de confianza asociado es (0,12978, 0,36403). La interpretación es similar en ambos casos: las dos variables presentan una asociación positiva y de intensidad baja.
Supuesto Práctico 21
Se realiza un estudio sobre la posible relación que hay entre la edad de las mujeres y su grado de aceptación de una ley sobre interrupción del embarazo. Para ello se ha realizado una encuesta sobre 450 mujeres cuyos resultados se adjuntan en la siguiente tabla:
\( \begin{array} {|c|ccc|} \hline & & Aceptación & \\ \hline Edad & Baja & Media & Alta \\ \hline 0-18 & 22 & 44 & 25 \\ \hline 18-30 & 36 & 41 & 25 \\ \hline 30-45 & 31 & 30 & 28 \\ \hline 45-65 & 37 & 26 & 23 \\ \hline > 65 & 40 & 30 & 12 \\ \hline \end{array} \)
Tabla 39: Datos del Supuesto Práctico 21 (.docx)
Contrastar al nivel de significación del 5% si existe relación entre el centro hospitalario y el motivo de las consultas. En caso afirmativo, dar medidas del grado de intensidad de dicha asociación.
Solución
En primer lugar, vamos a introducir los datos en R-Commander. Para ello, creamos un fichero de texto como el que aparece en la Imagen

Tabla 40: Datos del Supuesto Práctico 21 (.txt)
Como puede verse, en la primera fila introducimos el nombre de las variables entre comillas y separados por un espacio. A continuación, en las siguientes filas se van introduciendo los datos que aparecen en la tabla. Hay que tener en cuenta que las modalidades de las variables cualitativas hay que escribirlas entre comillas. Para que R-Commander tome en orden de menor a mayor las categorías del nivel de aceptación le ponemos delante un número de 1 al 3 de menor a mayor respectivamente. Si no hacemos esto, R-Commander toma el orden de las categorías por orden alfabético.
A continuación, cargamos el fichero creado mediante las siguientes instrucciones:
Datos/Importar datos/desde archivo de texto, portapapeles o URL…
Se muestra una ventana en la que introducimos el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Aborto. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Pulsamos a Aceptar y se muestra una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

Para transformar la tabla de contingencia en un conjunto de datos (data.frame) con elque R-Commander pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script, seleccionar las tres a la vez y darle a Ejecutar:
P<-rep(Ejemplo_Aborto$Edad,Ejemplo_Aborto$Frecuencia)
Q<-rep(Ejemplo_Aborto$Aceptacion,Ejemplo_Aborto$Frecuencia)
Edad_Aceptacion<-data.frame(P,Q)
Para visualizar el conjunto de datos en forma de lista deberemos pulsar en el botón Conjunto de datos y seleccionar el nuevo conjunto de datos creado, al que hemos llamado Edad_Aceptacion.
A continuación planteamos el contraste que se debe resolver para dar comprobar la dependencia o independencia de las variables.
\( H_0 \equiv \) La edad de las mujeres y el grado de aceptación de una ley sobre la interrupción del embarazo son independientes
\( H_1 \equiv \) La edad de las mujeres y el grado de aceptación de una ley sobre la interrupción del embarazo son dependientes
Y procedemos a resolverlo mediante la opción: Estadísticos/Tablas de contingencia/Tabla de doble entrada
Se muestra una ventana con dos pestañas.
- En la pestaña Datos tenemos que seleccionar las variables que queremos que aparezcan tanto por filas (en nuestro caso, la variable P a la que hemos asignado la edad) como por columnas (seleccionamos la variable Q a la que hemos asignado el grado de aceptación).
- En la pestaña Estadísticos tenemos la opción de incluir algún porcentaje en la tabla de doble entrada, aunque por defecto aparece sin porcentajes. En principio, lo vamos a dejar así. También aparece seleccionado el Test de independencia Chi-cuadrado, que es el que nos interesa. Por tanto, no modificamos ninguna de las opciones y le damos a Aceptar.
En la ventana de salida nos aparecen los siguientes resultados:
- En primer lugar, la tabla de doble entrada en la que se incluyen únicamente las frecuencias absolutas.
- A continuación nos aparece el estadístico de contraste del test (X-squared), los grados de libertad asociados al test (df) y el p-valor (p-value).
Frequency table:
Q
P 1_Baja 2_Media 3_Alta
0-18 22 44 25
18-30 36 41 25
30-45 31 30 28
45-65 37 26 23
65 o mas 40 30 12
Pearson’s Chi-squared test
data: .Table
X-squared = 18.037, df = 8, p-value = 0.02095
En este caso, el valor del estadístico de contraste es 18.037. Este estadístico de contraste sigue una distribución Chi-cuadrado con 8 grados de libertad. El p-valor asociado al contraste es, aproximadamente, 0.021 que, al ser menor que el nivel de significación (0.05) nos lleva a rechazar la hipótesis nula. Concluimos, por tanto, que la edad de las mujeres y el grado de aceptación de la ley sobre la interrupción del embarazo son variables que están relacionadas.
Determinemos ahora el grado de intensidad de esta relación. Dado que ambas variables son de tipo ordinal, las medidas que se van a calcular son el coeficiente gamma de Goodman y Kruskal, los coeficientes d de Somers, el coeficiente tau-b de Kendall y el coeficiente tau-c de Kendall.
Antes de calcular de estos coeficientes, se debe cargar el paquete DescTools (también será necesario instalar el paquete, en caso de no haberlo hecho con anterioridad).
Para cargar el paquete, en el menú seleccionamos: Paquetes/Cargar paquete…
Para poder trabajar desde R-Commander con el paquete, en la ventana RScript escribimos la instrucción
library(DescTools)
La seleccionamos y le damos a Ejecutar.
Una vez hecho esto, podemos calcular el coeficiente gamma de Goodman y Kruskal a través de la función
GoodmanKruskalGamma(x, conf.level = NA),
que tiene los siguientes argumentos:
- x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
- leveles el valor del nivel de confianza a partir del cual se calcula un intervalo de confianza para el coeficiente.
Para ello, en primer lugar escribimos la siguiente instrucción en R Script
> .Table <- xtabs(~P+Q, data=Edad_Aceptacion)
La seleccionamos y pulsamos Ejecutar. A continuación podemos calcular los coeficientes
En nuestro caso, escribimos en R Script la instrucción
> GoodmanKruskalGamma(.Table, conf.level = 0.95)
gamma lwr.ci upr.ci
-0.16467700 -0.26566503 -0.06368897
El valor del coeficiente gamma es de -0,164, lo que indica una asociación negativa y débil entre ambas variables. El intervalo de confianza para el coeficiente, a un nivel de confianza del 95% es (-0,265, -0,063).
Para obtener los coeficientes d de Somers, se utiliza la función SomersDelta(x, direction = c(“row”, “column”), conf.level =NA). Esta función tiene los siguientes argumentos:
-
x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
-
direction indica qué coeficiente de Somers se calcula. Por defecto, direction = “row”, lo que implica que la variable situada en las filas actúa como variable dependiente. Si se desea que la variable dependiente sea la situada en las columnas, basta con adjudicar el valor “column” a este argumento.
-
level es el valor del nivel de confianza a partir del cual se calcula un intervalo de confianza para el coeficiente.
Para calcular los coeficientes d de Somers en nuestro caso escribiremos:
> SomersDelta(.Table, direction =”row”, conf.level = 0.95)
somers lwr.ci upr.ci
-0.13220094 -0.21373760 -0.05066428
> SomersDelta(.Table, direction =”column”, conf.level = 0.95)
somers lwr.ci upr.ci
-0.10863303 -0.17547613 -0.04178993
Cuando la variable situada en las filas (edad) actúa como dependiente, el valor del coeficiente es -0,132, lo que indica una asociación negativa y baja entre las variables. Un intervalo de confianza al 95% para este coeficiente es (-0,213, -0,050).
Si la variable independiente es la situada en las columnas (grado de aceptación), el valor del coeficiente es –0,108, indicando, nuevamente una asociación negativa y baja entre las variables. En este caso, el intervalo de confianza para el coeficiente al 95% de confianza es (-0,175, -0,041).
Los coeficientes tau de Kendall (tau-b y tau-c) se calculan mediante las funciones
KendallTauB(x,conf.level=NA)
StuartTauC(x,conf.level=NA)
respectivamente. Los parámetros de estas funciones son los mismos:
-
x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
-
level es el valor del nivel de confianza a partir del cual se calcula un intervalo de confianza para el coeficiente.
Así, en nuestro ejemplo concreto, ambos coeficientes se calculan tal y como se indica a continuación:
> KendallTauB(.Table, conf.level = 0.95)
tau_b lwr.ci upr.ci
-0.11983901 -0.19361709 -0.04606094
> StuartTauC (.Table, conf.level = 0.95)
tauc lwr.ci upr.ci
-0.13017778 -0.21031807 -0.05003749
El valor del coeficiente tau-b de Kendall es –0,119, con un intervalo de confianza al 95% de confianza de (-0,193, -0,046). El coeficiente tau-c de Kendall toma un valor de -0,130 y el intervalo de confianza asociado es (-0,210, -0,050). La interpretación es similar en ambos casos: las dos variables presentan una asociación negativa y de intensidad baja.
Todos los coeficientes calculados toman valores bajos y negativos (entre -0.10 y -0.16, aproximadamente), siendo todos ellos significativos al 5% de significación. La significación de cada coeficiente se pone de manifiesto al no estar incluido el valor 0 dentro del intervalo de confianza que aparece en la salida correspondiente. Esto indica una asociación indirecta y débil (aunque significativa) entre las dos variables analizadas.
Se puede concluir, por tanto, que a medida que aumenta el rango de edad de las mujeres baja su nivel de aceptación de la ley y viceversa.
Supuesto Práctico 22
El ministerio de sanidad está interesado en conocer si hay relación entre el motivo de la consulta de los usuarios y el centro hospitalario al que recurren. Para ello, clasifican el motivo de la consulta en 7 grupos y realizan el estudio en 5 centros similares. Los 7 motivos de consulta se clasificaron en los siguientes grupos: (1) Medicina preventiva; (2) Enfermedades alérgicas; (3) Enfermedades respiratorias de vías altas; (4) Enfermedades respiratorias de vías bajas; (5) Enfermedades agudas; (6) Enfermedades crónicas; (7) Intoxicaciones. Los datos se muestran en la siguiente tabla:
\( \begin{array} {|c|ccccc cc|} \hline Centro & & & Tipo & de & consulta & & \\ \hline Hospitalario & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline 1 & 400 & 89 & 78 & 29 & 35 & 25 & 38 \\ \hline 2 & 328 & 56 & 89 & 7 & 59 & 34 & 52 \\ \hline 3 & 259 & 90 & 87 & 15 & 56 & 48 & 39 \\ \hline 4 & 324 & 156 & 75 & 63& 212 & 125 & 65 \\ \hline 5 & 123 & 89 & 12 & 27 & 34 & 23 & 18 \\ \hline \end{array} \)
Tabla 41: Datos del Supuesto Práctico 22 (.docx)
Contrastar al nivel de significación del 5% si existe relación entre el centro hospitalario y el motivo de las consultas. En caso afirmativo, dar medidas del grado de intensidad de dicha asociación.
Solución
Recordar que tenemos que introducir en R la siguiente instrucción
> library(Rcmdr)
para poder trabajar con R_Commander
En primer lugar, vamos a introducir los datos en R-Commander. Para ello, creamos un fichero de texto como el que aparece en la Imagen

Tabla 42: Datos del Supuesto Práctico 22 (.txt)
Como puede verse, en la primera fila introducimos el nombre de las variables entre comillas y separados por un espacio. A continuación, en las siguientes filas se van introduciendo los datos que aparecen en la tabla. Hay que tener en cuenta que las modalidades de las variables cualitativas hay que escribirlas entre comillas.
A continuación, cargamos el fichero creado mediante las siguientes instrucciones:
Datos/Importar datos/desde archivo de texto, portapapeles o URL…
En la ventana resultante introducimos el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Hospital. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Pulsamos Aceptar se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre “Ejemplo_Hospital” que le hemos asignado a nuestro conjunto de datos.
Para transformar la tabla de contingencia en un conjunto de datos (data.frame) con elque R-Commander pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script, seleccionar las tres a la vez y pulsar Ejecutar:
P<-rep(Ejemplo_Hospital$Centro,Ejemplo_Hospital$Frecuencia)
Q<-rep(Ejemplo_Hospital$Consulta,Ejemplo_Hospital$Frecuencia)
Centro_Consulta<-data.frame(P,Q)
Para visualizar el conjunto de datos en forma de lista deberemos pulsar en el botón Conjunto de datos y seleccionar el nuevo conjunto de datos creado, al que hemos llamado Centro_Consulta.
En Conjunto de datos aparece el nombre “Ejemplo_Hospital” que le hemos asignado a nuestro conjunto de datos.

A continuación planteamos el contraste que se debe resolver para dar comprobar la dependencia o independencia de las variables
\( H_0 \equiv \) El centro hospitalario y el motivo de la consulta son independientes
\( H_1 \equiv \) El centro hospitalario y el motivo de la consulta son dependientes
Y procedemos a resolverlo mediante la opción: Estadísticos/Tablas de contingencia/Tabla de doble entrada
Se muestra la siguiente ventana que consta de dos pestañas:
- En la pestaña Datos tenemos que seleccionar las variables que queremos que aparezcan tanto por filas (en nuestro caso, la variable P a la que hemos asignado el centro) como por columnas (seleccionamos la variable Q a la que hemos asignado el motivo de la consulta).
- En la pestaña Estadísticos tenemos la opción de incluir algún porcentaje en la tabla de doble entrada, aunque por defecto aparece sin porcentajes. En principio, lo vamos a dejar así. También aparece seleccionado el Test de independencia Chi-cuadrado, que es el que nos interesa. Por tanto, no modificamos ninguna de las opciones
Pulsamos Aceptar
En la ventana de salida nos aparecen los siguientes resultados:
- En primer lugar, la tabla de doble entrada en la que se incluyen únicamente las frecuencias absolutas.
- A continuación nos aparece el estadístico de contraste del test (X-squared), los grados de libertad asociados al test (df) y el p-valor (p-value).
Frequency table:
Q
P Agudas Alergias Cronicas Intoxicaciones Preventiva Vias Altas Vias Bajas
Hosp1 35 89 25 38 400 78 29
Hosp2 59 56 34 52 328 89 7
Hosp3 56 90 48 39 259 87 15
Hosp4 212 156 125 65 324 75 63
Hosp5 34 89 23 18 123 12 27
Pearson’s Chi-squared test
data: .Table
X-squared = 360.78, df = 24, p-value < 2.2e-16
El valor del estadístico de contraste, en este caso, es de 360.78. Este estadístico de contraste sigue una distribución chi-cuadrado con 24 grados de libertad. El p-valor asociado al contraste es prácticamente 0. Como este p-valor es menor que el nivel de significación considerado (0.05), se rechaza la hipótesis nula planteada, concluyendo la asociación entre el centro hospitalario y el tipo de consulta.
Una vez comprobada la relación entre las dos variables, pasamos a cuantificar su magnitud. Para ello, debemos tener en cuenta que ambas variables son nominales (pues no existe un orden preestablecido entre las categorías de cada una de ellas). Consecuentemente, las medidas de asociación que vamos a calcular son el coeficiente phi, el coeficiente de contingencia, el coeficiente V de Cramer y los coeficientes lambda.
Antes de calcular de estos coeficientes, se debe cargar el paquete DescTools (también será necesario instalar el paquete, en caso de no haberlo hecho con anterioridad).
Ya tenemos instalado el paquete, pero ahora hay que cargarlo para poder trabajar con él. En el menú seleccionamos:
Paquetes/Cargar paquete…
En la ventana Selectone que se abre, seleccionamos el paquete Desc Tools que acabamos de instalar y pulsamos Ok.
Para poder trabajar desde R-Commander con el paquete, en la ventana RScript escribimos la instrucción
library (DescTools)
Para ello, en primer lugar escribimos la siguiente instrucción en R Script
> .Table <- xtabs(~P+Q, data= Centro_Consulta)
La seleccionamos y pulsamos Ejecutar. A continuación podemos calcular los coeficientes
Una vez hecho esto, se calcula cada una de las medidas de asociación.
Una vez hecho esto, calculamos el coeficiente phi mediante la función Phi, que tiene un único argumento Phi (x), dondex es la tabla de contingencia a partir de la cual se calcula el coeficiente. En nuestro caso, escribiremos
Phi(.Table)
El coeficiente de contingencia se obtiene mediante la función ContCoef, cuyo argumento es el mismo que el de la función Phi, por tanto, escribiremos en R Script la instrucción
ContCoef(.Table)
Para obtener el coeficiente V de Cramer en R se utiliza la función CramerV, la cual, además de la tabla de contingencia, puede recibir como argumento opcional un nivel de confianza en cuyo caso calcula un intervalo de confianza para el coeficiente.
CramerV (x, conf.level = NA)
donde
- x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
- level es el valor del nivel de confianza a partir del cual se calcula un intervalo de confianza para el coeficiente.
El coeficiente V de Cramer para los datos de este ejemplo se obtiene escribiendo
CramerV(.Table, conf.level = 0.95)
Una vez escritas las instrucciones en R Scrpt, las seleccionadas y ejecutadas, en la ventana de resultados aparecen sus valores:
> Phi(.Table)
[1] 0.3327194
> ContCoef(.Table)
[1] 0.3157034
> CramerV(.Table, conf.level = 0.95)
Cramer V lwr.ci upr.ci
0.1663597 0.1434872 0.1784028
Según el coeficiente phi y el coeficiente de contingencia, la asociación entre las dos variables es moderada-baja. Esta asociación es baja si atendemos al valor del coeficiente V de Cramer (0.166).
Por último, el coeficiente lambda se calcula con la función Lambda, que tiene los siguientes argumentos:
Lambda (x, direction = c(“symmetric”, “row”, “column”), conf.level = NA)
donde
- x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
-
direction indica la versión del coeficiente que se calculará. Por defecto se calcula la versión simétrica del coeficiente (symmetric), en la que las dos variables desempeñan el mismo papel de manera que no se distingue entre variable dependiente y variable independiente. Si se selecciona el valor row para este argumento, la variable situada en las filas asume el papel de variable dependiente, mientras que si se selecciona el valor column, será la variable situada en las columnas la que ejerza el papel de variable dependiente.
- level es el valor del nivel de confianza a partir del cual se calcula un intervalo de confianza para el coeficiente.
En este ejemplo, para calcular el coeficiente lambda simétrico y los dos coeficientes lambda asimétricos escribimos en R Script las siguientes instrucciones respectivamente.
> Lambda(.Table, direction = c(“symmetric”), conf.level = 0.95)
lambda lwr.ci upr.ci
0.022145669 0.007930246 0.036361092
> Lambda(.Table, direction = c(“row”), conf.level = 0.95)
lambda lwr.ci upr.ci
0.04019652 0.01464059 0.06575244
> Lambda(.Table, direction = c(“column”), conf.level = 0.95)
lambda lwr.ci upr.ci
0 0 0
Por su parte, el coeficiente lambda simétrico indica una asociación muy baja entre las variables (aunque significativa). Cabe destacar el nulo poder predictivo del centro hospitalario sobre el tipo de consulta.
Supuesto Práctico 23
Se realiza un estudio para analizar si existe asociación entre los ingresos de un grupo de 132 trabajadores de varias empresas y su nivel de estudios. Se clasifica el salario que reciben en tres categorías: (Salarios están entre 700 y 999 euros; Salarios entre 1000 y 1500 euros y Salarios mayores de 1500 euros). El nivel de estudios se mide en tres categorías (estudios básicos, secundarios y universitarios). Los datos del ejercicio se recogen en la siguiente tabla:
\( \begin{array} {|c|c|} \hline & Nivel \hspace{.1cm}de \hspace{.1cm} estudios \\ \hline Salario & Básico \hspace{1cm} Secundarios \hspace{1cm} Universitarios \\ \hline 700-9999 & \hspace{-.5cm}26 \hspace{3cm} 9 \hspace{3cm} 5 \\ \hline 1000-1500 & \hspace{-.3cm} 13 \hspace{2.6cm} 18 \hspace{3cm} 12 \\ \hline > 1500 & 6 \hspace{3cm}8 \hspace{3cm} 25 \\ \hline \end{array} \)
Tabla 43: Datos del Supuesto Práctico 23
Contrastar, a un nivel de significación del 5% si ambas variables están relacionadas. En caso afirmativo, dar medidas para cuantificar la intensidad de dicha relación.
Solución
Recordar que tenemos que introducir en R la siguiente instrucción
> library(Rcmdr)
para poder trabajar con R_Commander
En primer lugar, vamos a introducir los datos en R-Commander. Para ello, creamos un fichero de texto como el que aparece en la Imagen

Tabla 44: Datos del Supuesto Práctico 23 (.txt)
En la primera fila introducimos el nombre de las variables entre comillas y separados por un espacio. A continuación, en las siguientes filas se van introduciendo los datos que aparecen en la tabla. Hay que tener en cuenta que las modalidades de las variables cualitativas hay que escribirlas entre comillas. Además, al ser ambas variables ordinales R-Commander toma el orden de las modalidades en orden alfabético y en el caso numérico la primera cifra de menor a mayor. Por tanto, vamos a indicar el orden de cada modalidad escribiendo antes de su nombre un número del 1 al 3, para indicar el orden de las modalidades de menor a mayor, respectivamente.
A continuación, cargamos el fichero creado mediante las siguientes instrucciones:
Datos/Importar datos/desde archivo de texto, portapapeles o URL…
En la ventana resultante introducimos el nombre que queremos asignarle al conjunto de datos con el que vamos a trabajar; en nuestro caso, escribiremos Ejemplo_Estudios. El resto de opciones las dejamos por defecto, ya que el archivo de texto que hemos creado cumple con todas ellas.
Pulsamos Aceptar se abre una ventana para que seleccionemos el archivo de texto que hemos creado y guardado anteriormente en nuestro ordenador. Cuando abrimos el archivo, podemos ver que en Conjunto de datos aparece el nombre que le hemos asignado a nuestro conjunto de datos.

Para transformar la tabla de contingencia en un conjunto de datos (data.frame) con elque R-Commander pueda trabajar hay que escribir las siguientes instrucciones en la ventana R Script, seleccionar las tres a la vez y pulsar Ejecutar:
P<-rep(Ejemplo_Estudios$Ingresos,Ejemplo_Estudios$Frecuencia)
Q<-rep(Ejemplo_Estudios$Estudios,Ejemplo_Estudios$Frecuencia)
Ingresos_Estudios<-data.frame(P,Q)
Para visualizar el conjunto de datos en forma de lista deberemos pulsar en el botón Conjunto de datos y seleccionar el nuevo conjunto de datos creado, al que hemos llamado Ingresos_Estudios
Pulsar Aceptar

Planteamos las hipótesis del contraste que debemos resolver:
\( H_0 \equiv \) El salario y el nivel de estudios son independientes
\( H_1 \equiv \) El salario y el nivel de estudios son dependientes
Y procedemos a resolverlo mediante la opción: Estadísticos/Tablas de contingencia/Tabla de doble entrada
Se muestra la siguiente ventana que presenta dos pestañas:
- En la pestaña Datos tenemos que seleccionar las variables que queremos que aparezcan tanto por filas (en nuestro caso, la variable P a la que hemos asignado los ingresos) como por columnas (seleccionamos la variable Q a la que hemos asignado el nivel de estudios).
-
En la pestaña Estadísticos tenemos la opción de incluir algún porcentaje en la tabla de doble entrada, aunque por defecto aparece sin porcentajes. En principio, lo vamos a dejar así. También aparece seleccionado el Test de independencia Chi-cuadrado, que es el que nos interesa. Por tanto, no modificamos ninguna de las opciones y le damos a Aceptar.
En la ventana de salida nos aparecen los siguientes resultados:
- En primer lugar, la tabla de doble entrada en la que se incluyen únicamente las frecuencias absolutas.
- A continuación nos aparece el estadístico de contraste del test (X-squared), los grados de libertad asociados al test (df) y el p-valor (p-value).
Frequency table:
Q
P 1_Basicos 2_Secundarios 3_Universitarios
1_70-999 26 9 5
2_1000-1500 13 18 12
3_1500 o mas 6 8 25
Pearson’s Chi-squared test
data: .Table
X-squared = 34.113, df = 4, p-value = 0.0000007066
El estadístico de contraste, que sigue una distribución chi-cuadrado con 4 grados de libertado, toma un valor de 34.113. El p-valor asociado al contraste es muy pequeño, menor que el nivel de significación (0.05), lo que nos lleva a rechazar la hipótesis nula. Concluimos, por tanto, que el salario y el nivel de estudios están relacionados o, dicho de otro modo, que existe un cierto grado de asociación entre las dos variables.
Pasemos ahora a cuantificar el grado de dicha asociación. Para ello, debemos tener presente que ambas variables son de tipo ordinal. Por tanto, calcularemos los 4 coeficientes de asociación que se han expuesto para este tipo de variables: gamma de Goodman y Kruskal, d de Somers, tau b de Kendall y tau c de Kendall.
Antes de calcular de estos coeficientes, se debe cargar el paquete DescTools (también será necesario instalar el paquete, en caso de no haberlo hecho con anterioridad).
Paquetes/Cargar paquete…
o bien escribir la siguiente instrucció en RGui
> library (DescTools)
Para poder trabajar desde R-Commander con el paquete, en la ventana RScript escribimos la instrucción
library(DescTools)
La seleccionamos y le damos a Ejecutar.
Una vez hecho esto, podemos calcular el coeficiente gamma de Goodman y Kruskal a través de la función
GoodmanKruskalGamma(x, conf.level = NA),
que tiene los siguientes argumentos:
- x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
- level es el valor del nivel de confianza a partir del cual se calcula un intervalo de confianza para el coeficiente.
Para ello, en primer lugar escribimos la siguiente instrucción en R Script
> .Table <- xtabs(~P+Q, data= Ingresos_Estudios)
La seleccionamos y pulsamos Ejecutar. A continuación podemos calcular los coeficientes
GoodmanKruskalGamma(.Table, conf.level = 0.95)
Para obtener los coeficientes d de Somers, se utiliza la función SomersDelta(x, direction = c(“row”, “column”), conf.level =NA). Esta función tiene los siguientes argumentos:
-
x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
-
direction indica qué coeficiente de Somers se calcula. Por defecto, direction = “row”, lo que implica que la variable situada en las filas actúa como variable dependiente. Si se desea que la variable dependiente sea la situada en las columnas, basta con adjudicar el valor “column” a este argumento.
-
level es el valor del nivel de confianza a partir del cual se calcula un intervalo de confianza para el coeficiente.
Para calcular los coeficientes d de Somers en nuestro caso escribiremos:
SomersDelta(.Table, direction =c(“row”), conf.level = 0.95)
SomersDelta(.Table, direction = c(“column”), conf.level = 0.95)
Los coeficientes tau de Kendall (tau-b y tau-c) se calculan mediante las funciones KendallTauB(x,conf.level=NA) y StuartTauC(x,conf.level=NA), respectivamente. Los parámetros de estas funciones son los mismos:
-
x es la tabla de contingencia a partir de la cual se calcula el coeficiente.
-
level es el valor del nivel de confianza a partir del cual se calcula un intervalo de confianza para el coeficiente.
Así, en nuestro ejemplo concreto, ambos coeficientes se calculan tal y como se indica a continuación:
KendallTauB(.Table, conf.level = 0.95)
StuartTauC (.Table, conf.level = 0.95)
En la pantalla de resultados aparecen los valores de los distintos coeficientes:
> GoodmanKruskalGamma(.Table, conf.level = 0.95)
gamma lwr.ci upr.ci
0.6183986 0.4477821 0.7890152
> SomersDelta(.Table, direction =c(“row”), conf.level = 0.95)
somers lwr.ci upr.ci
0.4413374 0.2999941 0.5826807
> SomersDelta(.Table, direction = c(“column”), conf.level = 0.95)
somers lwr.ci upr.ci
0.4393787 0.3007292 0.5780281
> KendallTauB(.Table, conf.level = 0.95)
tau_b lwr.ci upr.ci
0.4403569 0.3009032 0.5798107
> StuartTauC (.Table, conf.level = 0.95)
tauc lwr.ci upr.ci
0.4389949 0.2999530 0.5780368
Los coeficientes tau-b y tau-c de Kendall, con valores que rondan el 0.44, sugieren una asociación moderada, positiva y significativa entre ambas variables. Esto quiere decir que, a medida que aumenta el nivel de estudios aumenta también el rango salarial y viceversa. Según el coeficiente gamma de Goodman y Kruskal, que toma el valor 0.618, la intensidad de la asociación entre el salario y el nivel de estudios es aún mayor.
Por último, los coeficientes d de Sommers se interpretan del siguiente modo:
- Cuando se considera como variable dependiente la variable situada en las filas (el rango salarial), el valor del coeficiente d de Sommers es 0.441. Esto significa que, conocido el nivel de estudios de un individuo, se reduce en un 44.1% la probabilidad de cometer un error al predecir su rango salarial.
- Cuando la variable que se sitúa en las columnas (el nivel de estudios) es la que actúa como variable dependiente, el coeficiente d de Sommers toma el valor 0.439. Esto quiere decir que, conocido el rango salarial de un individuo, se reduce en un 43.9% la probabilidad de equivocarse al predecir su nivel de estudios.
- Los valores tan cercanos de ambos coeficientes nos llevan a concluir que las dos variables tienen un poder similar a la hora de predecir los valores de la otra.
Autoras: Beatriz Cobo Rodríguez, Silvia María Valenzuela Ruiz y Ana María Lara Porras. Universidad de Granada. (2022).